Some practical recommendations for the mass modification in structures examined by operational modal analysis
Algunas recomendaciones prácticas para realizar la modificación de masa en estructuras examinadas mediante análisis modal operacional
Abstract
The accuracy obtained in the estimation of the scaling factors
depends on the accuracy achieved in the identification of modal
parameters and the strategy of mass modification used
to alter the dynamic behaviour of the structure. At the same
time, the methodology for mass modification is based on the
magnitude, location and the number of masses added to the
structure. Throughout the presentation of this work, some
simple rules are proposed that can be used to define more
adequately the strategy of mass modification to be used in
the method of mass change for different types of structures.
Keywords
Operational modal analysis, scaling factor, mass change method.
Resumen
La exactitud obtenida en la estimación de los factores de escala
depende de la exactitud alcanzada en la identificación
de los parámetros modales y la estrategia de modificación de
masa utilizada para alterar el comportamiento dinámico de la
estructura. A su vez, la metodología para la modificación de
masa está basada en la magnitud, la ubicación y el número de
masas añadidas a la estructura. A lo largo de la exposición del
trabajo, se proponen algunas reglas sencillas, que pueden ser
utilizadas para definir de forma más adecuada la estrategia
de modificación de masa, a utilizar en el método de cambio de
masa, para diversas tipologías de estructuras.
Palabras clave
Análisis modal operacional, factores de escala, método del cambio de masa.
Recibido / received: 29.10.2018. Aceptado / accepted: 18.11.2018.
Introduction
Parloo et al. (2002) proposed that the
scale factor that relates the standardized
and non-standardized vibration
modes , be determined
by introducing mass change, defined
by the mass change matrix and
applying the expressions (1) and (2)
and w0, w1 are the natural frequencies
of the mode under consideration,
before and after the application
of the mass change. If the mass change
matrix is proportional to the original
matrix, then the vibration modes do
not change, and the above equation
represents an accurate linear elastic
solution to the relationship between
the mass change, frequency deviation,
and the scale factor of the mode of vibration
(Parloo et al., 2002; Braun and
Ram, 2001). However, in the event
that the mass change matrix were not
proportional to the initial mass matrix,
the above equation would only be
an approximation.
It can be shown that, to reduce the
uncertainty in the estimation of the
scaling factors, errors in the estimation
of the modal parameters (Villa
2007; Villa 2008; Villa 2009a) should
be minimized during the pilot phase
of the modal analysis, as well as the
difference between the modes of vibration,
modified and unmodified
(Brincker and Andersen, 2003; López
et al., 2005; Villa, 2014; Villa 2015).
The difference between original
and modified modes of vibration is minimized
if (Parloo et al., 2005; López
et al., 2007):
– A large number of masses is added to the structure.
– The masses are well distributed.
– The masses are located in optimal positions (peaks and valleys of the modes of vibration).
– The magnitude of the mass change is small.
Types of error and ways of reducing it
When using the expression proposed
in the preceding paragraph (Parloo
et al., 2002; Brincker and Andersen,
2003) for the determination of the
scale factors, three sources of error
emerge:
a) Systematic errors due to changes in the modes of vibration.
b) Random frequency deviation errors.
c) Random vibration modes errors.
From what has already been explained,
it follows that the best solution
in order to reduce errors introduced
by changes in the modes of vibration
is the modification of mass, so that all
the degrees of freedom experience the
same relative change in mass. This
approach presupposes that, prior to
conducting the trial, a reliable estimate
of mass distribution in the structure
should be made.
Therefore, it can be concluded that
scaling factors should be determined
through mass changes as spread out as
possible (Hang et al., 2008; Hang et
al., 2009), so that the resulting changes
in the natural frequencies are large,
compared to the uncertainty of the
natural frequencies (Brincker and Andersen,
2003).
That is, several goals which are
opposing each other must be met simultaneously.
On the one hand, mass
change must be high, in order to maximize the frequency deviation, but on the other, it must also be low in order to minimize changes in the modes of vibration (Bernal, 2004; Khatibi et al., 2009; Khatibi et al., 2012; Zhanget al., 2005).
Practical recommendations for mass modification
Operational trials constitute an advantageous alternative for the calculation of the modal characteristics of constructions (NCSE, 2002), according to the NCSE-2002 Spanish regulations.
The standard for earthquake-resistant construction NCSE-2002 (general guidelines and construction) with regards to the dynamic calculation through the response spectra analysis, prescribes that the calculation of the modal characteristics of construction (Villa, 2004a; Villa 2006; Villa, 2009b; Villa, 2004b) can be carried out —preferably and in order of preference— taking into account:
– Tests made on constructions with characteristics equal or similar to the ones being studied.
– Tests made on models of the construction considered.
– Theoretical procedures of structural mechanics.
– Approximate or empirical formulas, see (NCSE, 2002).
Previous estimates
To identify favorable positions of the sensor/s of reference —for one or more modes of interest— it is sufficient to locate the rows of the modal matrix in which the displacement corresponding to that floor or degree of freedom, in the mode/s that are to be identified, are the largest possible. In this regard, a prior finite element analysis of the vibration modes of the structure before its experimental analysis provides an initial approximation to the modes of interest, the degrees of freedom that define them (Emin et al., 1997; Moller et al. 2000; Brincker and Andersen, 1999), the sets of data required and the location and number of reference sensors, so that all measured directions are reliably represented in all data sets.
On the other hand, once the actual experimental modal parameters of the structure have been determined, and in order to make the following test/s with the modified mass (Black et al., 1997; Villa, 2005), it is suitable to determine an estimate of the distri–bution of mass in the structure before carrying out said tests. Taking this estimate into account, the modification of mass could be made in such a way that all the degrees of freedom that are affected by it would have very similar relative mass changes, resulting in a reduction of the errors introduced by changes in the modes of vibration.
Modification of mass in different types of structures
Listed below are some proposed solutions for the modification of mass on structures of different types.
a) Building structures
These structures consist of slabs or floor plates, beams and columns. In some cases, screens or stiff cores are added to the latter.
– In general, the measurements of interest tend to be the lateral movements of the floors of the building. It is necessary to select the proper locations for the sensors in order to isolate the components of translation and torque in the movement of each floor. It follows from here that there are directions in which the movement is not going to be measured, but it can be inferred by assuming that each floor is infinitely rigid in its plane. These movements, although deduced, improve the appearance of the modes of vibration (Ventura and Schuster, 1996).
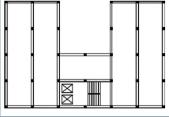
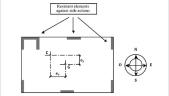
– In the event that some type of floor symmetry (one or two orthogonal axes) were present, it is suitable to take it into account when placing masses on each of the different levels since, if the mass distribution is symmetric, the moments of inertia resulting around the two main axes of inertia contained in the plane of the slab will be the same. Floor sections with a single axis of symmetry (Figure 1) or without symmetry (Figure 2) mean that the centers of mass and stiffness (also called the center of torque or shear) will be different. These sections are not suitable for calculations through the simplified methods described by various standards of dynamic analysis, giving rise to hard to evaluate internal forces as a result of the emergence of actions of torque coupled with flex (Villa, 2002; Villa, 2004c). I.e., at any level of a building, the oscillation-induced force of inertia acts through the center of mass of the upper levels, while the result of all the resistant forces acts in the center of stiffness of the resistant elements of the level under consideration. If the structure does not have dynamic symmetry, the center of stiffness on a given floor and the center of mass above it do not match. In these circumstances a torque moment is generated in the floor. This torque moment in the floor is equal to the product of the shear force of the floor multiplied by the eccentricity, calculated as the distance between the top center of mass and the center of stiffness of the floor. This distance is measured in the direction normal to the oscillations. Figure 3 shows the eccentricities e and e between the center of mass G and the center of stiffness C, induced by the stiff core and screens, for oscillations acting in the North-South and East-West directions, respectively (Paz, 1992). Therefore, in general, whenever the construction presents symmetry, it is convenient to maintain it when applying additional mass to perform the mass-change method; It’s easy to observe, however, that on numerous occasions this symmetry is not present in the initial design.
On the other hand, in a building with floor symmetry, where the mass is placed maintaining this symmetry at each level, masses need to be placed as far as possible from the center of mass of each floor, i.e. in its perimeter, if it is desired to obtain a greater sensitivity to the torque oscillations.
Even in some situations in which the center of mass coincides with the torque, as happens in very elongated floors (Figure 4), it should be noted that there can be natural frequencies
of translation coupled with the
ones from torque (NCSE, 2002).
– If theoretical procedures of structural
mechanics, instead of tests,
are used to obtain the modal characteristics
of the construction, it
is necessary to take into account if
the construction is clear or highly
compartmentalized. In this case,
it is necessary to consider the collaboration
of the non-structural
elements in the stiffness of the construction
(in the case of buildings:
walls, partition walls, stairs, etc.). In
this regard, the simplified methods
described in EUROCODE 8 offer
a reasonable estimate of the reduction
of the natural period caused
by the addition of these elements
(UNE-ENV 1998-1-3:2000 Eurocódigo
8).
– In tall buildings (20 floors, for example), it should be taken into account that it is frequent for flex modes to appear coupled with torque.
b) Bridges
Two kinds of bridges, cable-stayed bridges and box girder bridges, are considered:
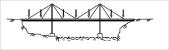
– Cable-stayed bridges: The blocks for mass modification should be placed close to the anchorages between the tensioning cables and the deck of the bridge, in order to avoid local oscillations of the sections between two anchors which would superimpose the global oscillations for the whole bridge (Figure 5). I.e., it is suggested to place point masses in the areas of greater stiffness of the board.
– Girder bridges: This section refers to bridges, either metallic, pre-stressed concrete or mixed, but mainly to the first ones, since they are more sensitive to the location of the mass modification because of their greater flexibility.
The latter type consists of a structural system of asymmetric continuous drawer beam, fully metallic, where the edge can be variable.
As was mentioned in the previous subsection, it is convenient to place the blocks (point masses for mass modification), on the stiffest points of the cross sections, which generally correspond to the upper vertices of the trapeze, and especially those sections where a transverse stiffening (Figure 6) framework is present, in order to avoid the influence of local fluctuations of the elements of the board in the total response. On the other hand, if a greater sensitivity to the torque oscillations in the analysis is also desired, it is advisable to have the point masses placed far from the axis of the roadway.
General recommendations
Finally, here are some general recommendations that may be useful in the majority of structural types:
– The location of the changes of mass at, or near, a nodal point of the eigenvector considered for the determination of the scale factor should be avoided. The resulting change in the natural frequency with respect to the initial conditions before mass changes, will be very small. In practice, mass changes for large structures are generated through the addition of heavy concrete blocks with a certain size and at a given position. It must be taken into account that, apart from modifying the mass, these blocks can also introduce changes in stiffness, which will cause errors that affect the determination of the scale factors. Thus, the dimensions of these blocks should be as small as possible.
– In the case of buildings, it is common in various seismic standards to allow a reduction of the masses that correspond to overloads of use of around 10%. Because of the reduced participation of the masses associated with the overloads of use in the movement of the building, since the masses can slide as they are not linked to the building, this reduction to their value is allowed (Villa, 2009b). However, the seismic actions show a remarkable level of oscillation. If the conditions of actual operation of the structure —or the conditions of the test— are very different from the traditional “soft” natural excitements applied in operational tests (caused by the traffic of vehicles, pedestrians, gusts of wind, etc.), the linking of the additional mass to the structure must be taken into account.
– Following up from the previous point, as well as the displacement of point masses in large blocks, care should be taken regarding possible oscillations on its supporting plane, so as not to increase the level of noise in the signal.
– The location of the blocks, placed near the sensors, can also be a source of error when the not match its center of mass is not coincidental with the degree of freedom (location of the sensor).
Conclusions
All recommendations outlined in the various paragraphs above are synthesized in that, to achieve an optimal distribution of modification of mass when implementing the method of mass change in operational modal analysis, special attention must be paid to how the inertial properties of the structure are modified, keeping consistency with its spatial distribution of mass and stiffness all along its geometry.
References
Bernal, D. (2004). Modal Scaling from Known Mass Perturbations, Journal of Engineering Mechanics, 130 9, 1083-1088.
Black, C., Tsai, P., Ventura, C. E. (1997). Ambient Vibration Measurements of the University Drive / Crowchild Trail Bridge in Calgary, Alberta, ISIS Canada, U. B. C. Earthquake Engineering Research.
Braun, S. G., Ram, Y. M., (2001). Modal modification of vibrating systems: some problems and their solutions, Mechanical Systems and Signal Processing (2001) 15(1), 101-119.
Brincker, R., Andersen, P. (2003). A Way of Getting Scaled Mode Shapes in Output Only Modal Analysis, In Proc. Of the International Modal Analysis Conference (IMAC) XXI, paper 141.
Brincker, R., Andersen, P. (1999). Ambient Response Analysis, Modal Analysis for Large Structures, Proceedings of The International Congress On Sound and Vibration Technical University of Denmark Lyngby.
Emin Aktan, A., Farhey, D. N., Helmicki, A. J., Brown, D. L., Hunt, V. J., Lee K., Levi, A. (1997). Structural Identification for Condition Assessment: Experimental Arts, Journal of Structural Engineering, december 1997.
Hang, H., Shankar, K., Lai, J. C .S. (2008). Prediction of the effects on dynamic response due to distributed structural modification with additional degrees of freedom, Mechanical Systems and Signal Processing 22 (2008), 1809-1825.
Hang, H., Shankar, K., Lai, J. C. S. (2009). Effects of distributed structural dynamic modification with reduced degrees of freedom, Mechanical Systems and Signal Processing 23 (2009) 2154-2177.
Khatibi, M. M., Ashory, M. R., Malekjafarian, A. (2009). Scaling of Mode Shapes Using Mass-Stiffness Change Method. Proceedings of the International Operational Modal Analysis Conference (IOMAC), Copenhagen.
Khatibi, M. M., Ashory, M. R., Malekjafarian, A., Brincker, R. (2012). Mass–stiffness change method for scaling of operational mode shapes, Mechanical Systems and Signal Processing 26 (2012), 34-59.
López Aenlle, M., Brincker, R., Canteli, A. F., García,
L. M. V. (2005). Scaling Factor Estimation by Mass Change Method, Proceedings of the 1st International Operational Modal Analysis Conference (IOMAC), Copenhagen, Denmark.
López Aenlle, M., Fernández, P. F., Brincker, R., Canteli A. (2007). Scaling Factor Estimation Using An Optimized Mass Change Strategy, Part 1: Experimental Results, Proceedings of The 2nd International Operational Modal Analysis Conference (IOMAC), Copenhagen, Denmark.
Ministerio de Fomento. Norma de Construcción Sismorresistente NCSE-02. Parte General y Edificación. España, 2002.
Moller, N., Brincker, R., Herlufsen, H., Andersen, P. (2000). Modal Testing of Mechanical Structures Subject to Operational Excitation Forces, Proceedings of The ISMA25 Noise and Vibration Engineering Volume 11. Leuven, Belgium, pp. 1315, september , 2000.
Paz, M. (1992). Dinámica Estructural Teoría y Cálculo, Reverté.
Parloo, E., Verboven, P., Guillaume P., Van Overmeire
M. (2002). Sensitivity-based operational mode shape normalization, Mechanical Systems and Signal Processing (MSSP) 16 (5) (2002), 757-767.
Parloo, E., Cauberghe, B., Benedettini, F., Alaggio, R., Guillaume, P. (2005), Sensitivity-based Operational Mode Shape Normalisation: Application to a Bridge, Mechanical Systems and Signal Processing (MSSP) 19 (2005), 43-55.
UNE-ENV 1998-1-3:2000 Eurocódigo 8: Condiciones de diseño para estructuras sismorresistentes. Parte 1-3: Reglas generales. Reglas específicas para distintos materiales y elementos.
Ventura, C. E., Schuster, N. D. (1996). Structural Dynamic Properties of a Reinforced Concrete High-rise Building During Construction, Can. J. Civ. Eng. nº 23, 950-972.
Villa García, L. M. (2002). Diseño Sísmico Conceptual de Estructuras Porticadas, Técnica Industrial, IV, 247, 54-66.
Villa García, L. M. (2004a). Aplicación de la Normativa de Construcción Sismorresistente, Técnica Industrial, I, 252, 60-67.
Villa García, L. M. (2004b). Aplicación de la Futura Normativa de Construcción Sismorresistente Europea, Dyna, vol. 79, nº 8, 35-41.
Villa García, L. M. (2004c). Diseño y Análisis Sismorresistente de Estructuras de Edificación. Ed. Bellisco, Ediciones Técnicas y Científicas.
Villa García, L. M. (2005). Identificación Modal Mediante Ajuste Local de la Respuesta, Publicación de Investigación CIMNE (Centro Internacional de Métodos Numéricos en Ingeniería) nº 271.
Villa García, L. M. (2006). Analogía de las normativas sismorresistentes española y europea, Técnica Industrial, I, 261, 26-32.
Villa García, L. M., (2007). Aplicación de Técnicas de Optimización para la Determinación de Parámetros Modales a través de las Funciones de Respuesta en Frecuencia. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, Vol. 23, nº 4, 395-414.
Villa García, L. M., (2008). Cálculo de la Matriz Modal de un Sistema Dinámico a partir de las Constantes Modales Utilizando Técnicas de Optimización, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, Vol. 24, nº 1, 13-23.
Villa García, L. M., (2009a). Determinación de parámetros modales a través del ajuste global de la respuesta, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, Vol. 25, nº 3, 207-225.
Villa García, L. M. (2009b). Algunas Consideraciones sobre la Futura Instrucción de Acero Estructural EAE en lo Referente al Proyecto de Estructuras Sismorresistentes, Dyna, vol. 84, nº 5, 393-402.
Villa García, L. M. (2014). Análisis de sensibilidad aplicado a la dinámica de estructuras mediante la modificación de las propiedades inerciales. Rev. Fac. Ing. Univ. de Ant. nº 70, 66-74.
Villa García, L. M., (2015). Error analysis in obtaining scale factors with operational modal analysis and mass change. Rev. Fac. Ing. Univ. de Ant. nº 75, 84-92.
Zhang, Y., Zhang, Z., Xu, X., Hua, H. (2005). Modal parameter identification using response data only, Journal of Sound and Vibration 282 (2005), 367-380.