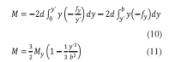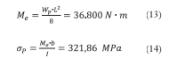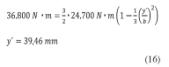Simulación numérica de las tensiones residuales generadas en una viga sometida a flexión
Numerical simulation of residual stresses generated in a beam subjected to bending
RESUMEN
El objetivo del presente trabajo consiste en el estudio de las tensiones
residuales (internas) que se producen en elementos estructurales,
originadas por sobreesfuerzos. Para su estudio se ha planteado,
inicialmente, la determinación de las tensiones residuales
partiendo de los criterios basados en la resistencia de materiales;
para posteriormente realizar una simulación numérica que nos
permita comparar los resultados obtenidos y así validar el método
numérico. Esta modelización se ha realizado utilizando el software
comercial de elementos finitos ABAQUSTM (v. 6.12).
Recibido: 11 de abril de 2013
Aceptado: 28 de junio de 2013
Palabras clave
Simulación, fatiga de materiales, flexibilidad, código técnico de edificación, cálculos, software
ABSTRACT
The aim of this work is the study of residual stresses (internal) that
occur in structural elements, caused by an overload. To achieve
this goal, firstly the residual stress state is determined by using
classic strength of materials criteria. Later, in order to validate the
results of the numerical simulation by using a commercial FEM
software (ABAQUSTM, v.6.12), they were compared with those given
by theoretical equations.
Received: April 11, 2013
Accepted: June 28, 2013
Keywords
Simulation, material fatigue, flexibility, technical building code, calculations, software
Introducción
En la aplicación de la teoría elástica la capacidad de carga de cualquier elemento de una estructura se supone que está limitada por la fluencia del material. Sin embargo, aun con un diseño elástico, cierta fluencia localizada tal como la debida a una concentración de tensiones es frecuentemente despreciada, lo que hace que se desprecie la posible fluencia.
Una aproximación muy simplificada de la deformación en el punto de fluencia en aceros (material dúctil por excelencia en el campo de las estructuras) es la aparición de las bandas de deslizamiento, denominadas líneas de Lüeder. Estas bandas o planos están con frecuencia en la dirección de la tensión cortante máxima.
El material que se ha deformado origina, a la vez, una concentración de tensiones en el cuerpo deformándose más, sin aumento, o con poco aumento de la carga. El proceso continúa hasta que el material se deforma inelásticamente. Este deslizamiento se produce normalmente a lo largo de los planos determinados por la orientación cristalina.
En los materiales elásticos, en particular en los metales, sabemos que un esfuerzo uniaxial lleva aparejado, inicialmente, un comportamiento elástico. Según la Ley de Hooke, esto significa que pequeños incrementos en la tensión dan lugar a pequeños incrementos en la deformación. Si deja de actuar la carga el cuerpo recupera exactamente su forma original, es decir, se tiene una deformación completamente reversible. Sin embargo, se ha comprobado experimentalmente que existe un límite, llamado límite elástico, tal que, si cierta función homogénea de las tensiones supera dicho límite entonces, al desaparecer la carga, quedan deformaciones remanentes y el cuerpo no vuelve exactamente a su forma. Es decir, aparecen deformaciones no reversibles y, en consecuencia, tensiones internas denominadas “residuales”. Estos materiales no fallan hasta que no se llega a una cuantía apreciable de la fluencia, lo que hace que la capacidad de carga de estos elementos estructurales pueda ser determinada más realmente extendiendo el análisis de tensiones dentro del periodo elastoplástico. Esto nos indica que la capacidad de carga de muchos materiales no está necesariamente limitada por la fluencia. Pero también es necesario indicar que, aunque al material se le podría someter a un esfuerzo adicional, hay que tener en cuenta que podría sobrevenir una deformación excesiva, lo cual haría peligrar las condiciones de servicio de la estructura.
Si tenemos en cuenta la normativa nacional que regula las estructuras empleadas en la edificación (CTE) –la cual, por cierto, incluye numerosos coeficientes de seguridad–, esta hace que el análisis estructural sea relativamente sencillo, ya que se efectúa dentro del periodo elástico del material. Ahora bien, si las cargas aumentan o bien la capacidad resistente de las estructuras disminuye (fluencia), se pueden llegar a desarrollar deformaciones no reversibles. Aunque al dimensionar las piezas en la condición del estado límite último (ELU) se tiende a considerar solamente las tensiones debidas a cargas novales, puede aparecer algún problema si, por ejemplo, aparecen cargas repetidas a las que no se suman las tensiones residuales, lo cual puede llegar a modificar el diseño si se las tiene en cuenta.
Aunque las situaciones de sobrecarga no son muy frecuentes, estas se pueden producir por diversas causas:
– Durante el proceso de diseño:
• Cargas accidentales
• Sobrecargas de uso
• Sismo
– Procesos de conformación, moldeo, mecanizado, soldadura, etc.
– Por motivos resistentes:
• Envejecimiento
• Fatiga
• Fuego
De las tensiones residuales o internas que se generan en los materiales, fundamentalmente dúctiles, por razones que a nadie se le escapan, son estudiadas principalmente, según la literatura actual, las que provienen de procesos de conformado y fabricación; básicamente en moldeado, mecanizado y soldadura. Es decir, los estudios de las tensiones residuales se centran en la preparación de la estructuras, pero, en determinados casos, las tensiones residuales se pueden introducir en las estructuras, bien sea en su instalación y montaje (lo cual también puede ser previsto), o bien sea por cargas muertas y/o por sobrecargas que puedan incidir en la estructura a lo largo de su periodo de vida en servicio.
Modelo simplificado de comportamiento elastoplástico a flexión pura de vigas
Teniendo en cuenta la teoría clásica de la resistencia de materiales de la que se deduce que:
siendo σ la tensión, M el momento flector actuante, “y” la distancia al eje neutro e “I” el momento de inercia de la sección transversal.
Esta ecuación supone que la Ley de Hooke es aplicable para todo elemento, siempre que la carga se aplique de forma progresiva y se mantenga constante en el tiempo. Si esta carga va aumentando de una manera progresiva, o si el material llega a hacerse frágil, se puede llegar a superar el límite de fluencia del material, con la aparición de un diagrama no lineal entre el esfuerzo y la deformación. Esto hace que la relación expuesta en la primera ecuación no sea válida.
Si quisiéramos buscar un procedimiento que generalizara la obtención de la distribución de esfuerzos en un elemento sometido a flexión pura y para el cual no podría usarse la Ley de Hooke, tendríamos que tener en cuenta algunos cambios:
– El eje neutro no necesariamente pasa por el centro de la sección. Solamente lo hará cuando la sección sea simétrica, tanto horizontal como verticalmente, y el material se caracterice por tener la misma relación entre la tensión y la deformación. Si este no pasa por el centro será necesario localizarlo mediante aproximaciones sucesivas hasta que la distribución de esfuerzos pueda satisfacer las condiciones de equilibrio:
Momento alrededor del eje z:
siendo σ la tensión, “y” la distancia al eje neutro y “A” la superficie de la sección transversal.
– En el análisis plástico se acepta el equilibrio estático hasta llegar a un estado de plasticidad total, verificando la hipótesis de Bernoulli sobre la conservación de las secciones planas durante el proceso de plastificación. El hecho de que la hipótesis de Bernoulli se mantenga hace que la distribución de la deformación unitaria siga siendo lineal, lo que indica que el alargamiento o acortamiento de una fibra es proporcional a la distancia “y” de la fibra al eje neutro. Ahora bien, la distribución de las tensiones en la fibra ya no es lineal, sino que tiene una forma como la que aparece en la figura 1.
Continuando con nuestro análisis teórico, si observamos la curva de esfuerzo-deformación, es simétrica con respecto al origen de coordenadas, ya que la distribución de εx es lineal y simétrica con respecto a dicho eje, como se observa en la figura 2.
A la vez, la distribución de la tensión y de la deformación en la sección transversal, la podemos estudiar si conocemos la tensión σp, ya que podemos determinar el valor εp, según ecuación 4 y cuyo resultado se puede ver en las figuras 3 y 4.
(Tang et al., 1998) Siendo εx la deformación en dirección “x”, εp la deformación elástica, “c” e “y” las distancias del eje neutro a las fibras.
Veamos analíticamente cómo se desarrolla el concepto para un caso concreto. Supongamos que tenemos una viga cargada que tiene una sección rectangular. Según la distribución de esfuerzos mostrados en la figura 4, esta se podría expresar de la siguiente forma (Beer et al, 2001):
siendo “d” el ancho de la viga y σ, una función impar de “y”, podríamos expresar:
Esta integral representa el primer momento con respecto al eje horizontal de la sección, el cual se limita por la curva de distribución de esfuerzos.
Con la finalidad de simplificar el análisis, el diagrama tensión-deformación lo llevamos a un estado elástico-plástico teórico como se puede observar en la figura 5.
Como se puede observar en el diagrama, mientras no se supere el límite de fluencia del material, el comportamiento del elemento estructural se va a regir por la Ley de Hooke y, por tanto, se verifica la ecuación 1, y el momento vendrá dado por:
siendo “I” el momento de inercia de la sección, “b” la distancia a la fibra más alejada y “fy”, la tensión en el límite elástico.
Como el valor de My es el mayor momento elástico que puede llegar a soportar la sección, de modo que si ese momento sigue aumentando, en las zonas más alejadas de la sección, se van a desarrollar fibras plastificadas, pero sigue existiendo un núcleo elástico, en el cual la tensión σx variará linealmente con la distancia “y”.
Como la sección analizada es una sección rectangular, la ecuación 7 la podemos expresar:
siendo “d” y “b” las dimensiones de la sección transversal de la sección.
La dimensión del núcleo elástico, que tiene una tensión σx, varía linealmente a lo largo de la sección hasta llegar a la zona plástica y la podemos determinar mediante la siguiente relación:
donde “y´” es distancia a la mitad del núcleo elástico.
Entonces, el diagrama con el que nos encontramos es el siguiente (figura 6).
Si ahora integramos la ecuación 6 teniendo en cuenta los dos tramos que tenemos en el esquema y las ecuaciones 8 y 9, obtenemos (Beer et al., 2001):
Ahora bien, si la carga sigue aumentando hasta llegar a plastificar toda la sección, implicaría que el valor de y´tendería a cero y, por tanto, la ecuación quedaría de la siguiente forma:
Apliquemos los conceptos expuestos al siguiente ejemplo:
Supongamos que tenemos una viga simplemente apoyada, con la forma y sección que muestra la figura, apoyada en sus extremos y sometida a una carga distribuida. Supongamos que la viga es de acero con un límite de fluencia del material de 240 MPa y un módulo de elasticidad de 200 GPa (figura 7).
Elásticamente, según ecuación 1:
Determinación del núcleo elástico según la ecuación 7:
Según ecuación 11:
Teniendo en cuenta el principio de superposición, representamos las tensiones (figura 8).
Ahora veamos la comprobación numérica de este ejemplo.
Simulación numérica
Los modelos simplificados permiten conocer el comportamiento global de una estructura con un reducido coste computacional, como hemos podido comprobar en los cálculos realizados anteriormente. Ahora bien, para poder conocer los estados tensionales en un determinado punto de una estructura, es necesario recurrir a modelos numéricos más complejos, aunque el coste computacional sea mayor.
En la simulación numérica, desde un punto de vista teórico, sin utilizar un software, se puede atacar el problema resolviendo el conjunto de ecuaciones no lineales que rigen el comportamiento elastoplástico. Uno de los procedimientos que se utiliza es el método de Newton-Raphson. Esta forma de operar requiere caracterizar el comportamiento elastoplástico de la viga mediante las matrices de rigidez secante y tangente asociadas a los distintos estados de equilibrio.
El desarrollo experimentado por los códigos de simulación numérica durante los últimos años, ha provocado la aparición de modelos de comportamiento mecánico para diferentes tipos de materiales que tienen en cuenta distintas formas para poder determinar estados tensionales en cualquier punto de un elemento estructural.
Para comprobar la precisión de los modelos simplificados se ha empleado un modelo de elementos finitos utilizando el código comercial ABAQUSTM (versión 6.12). El modelo es tridimensional, y se ha desarrollado íntegramente en ABAQUS/Standard utilizando el algoritmo *MODEL CHANGE (Nagtegaal et al., 1991) (Boyceet al., 1995).
Las propiedades del material empleado son las de la tabla 1.
Para intentar realizar una comprobación con los valores teóricos obtenidos en el problema, es necesario indicar que la sección que tiene la viga no se ha elegido al azar; se ha seleccionado para que presente una esbeltez adecuada y de este modo dominen las tensiones provocadas por la flexión pura.
Para la malla que se ha empleado en este modelo se han elegido elementos cúbicos de integración reducida de ocho nodos C3D8R de ABAQUS. Se ha realizado una convergencia de malla y una convergencia del paso, para que ambas variables no intervengan en el resultado final (figura 9).
Modelo numérico: ABAQUS Standard
En este modelo tridimensional se ha determinado el problema de la viga según Static Standard que tiene implementada el software. En el proceso de análisis se han tenido en cuenta los efectos no lineales (Nlgeon).
En cualquier análisis estático la carga siempre se introduce de forma gradual. Esto es un aspecto esencial que tener en cuenta, pues si no, no se cumplirían muchos de los principios de la resistencia de materiales. En este modelo la carga, según está implementada en el software, se introduce de forma progresiva (Ramp) y, por tanto, no tenemos que preocuparnos de modificar su estado.
Para poder obtener las tensiones residuales (internas) que se han generado en el material, después de la recuperación elástica empleamos el algoritmo *MODEL CHANGE, que nos permite, sin tener que realizar una exportación del modelo, obtener la recuperación elástica o *SPRINGBACK (Tang et al., 1998). Por definición, springback es la “condición que se produce cuando un metal laminado o aleación tiene una tendencia a retornar parcialmente a su forma original debido a su recuperación elástica. Esta recuperación elástica está influenciada también por el espesor, el radio y ángulo de curvatura” (definición recogida según normas ASTM, DIN, EN, etc.).
Como hemos podido comprobar en el análisis, por las teorías clásicas de la resistencia de materiales, la carga es lo suficientemente elevada como para que se supere el límite elástico y, por tanto, cuando se llega al springback existen un grupo de fibras que no recuperan su estado inicial, acumulando en su interior tensiones internas (residuales) que son las que se reflejan en el estudio teórico y, como se verá, aparecen en las gráficas obtenidas a partir de esta simulación.
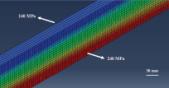
En la figura 10 se pueden apreciar los estados tensionales cuyo diagrama policromático nos revela las fibras que están comprimidas y las que están traccionadas. El color azul intenso indica que esas fibras han llegado a la tensión de fluencia del material por compresión mientras que el color rojo intenso muestra las fibras que han alcanzado la tensión de fluencia por tracción.
Si tomamos la sección plana correspondiente al centro geométrico de la viga podremos visualizar la evolución de las tensiones, como se puede comprobar en las figuras 11, 12 y 13.
Resultados
En las gráficas en las figuras 14, 15y 16, se han representado de forma conjunta los valores obtenidos en la simulación numérica mediante FEM con ABAQUS, y los obtenidos teóricamente utilizando los principios de la resistencia de materiales clásica para la flexión pura.
Como se puede comprobar, los resultados de la simulación numérica y los teóricos presentan una gran aproximación. Si comenzamos analizando los resultados dentro del periodo elástico del material, tanto la simulación numérica como el cálculo teórico son exactamente iguales. Este resultado es muy lógico ya que todas las relaciones entre la tensión y la deformación son lineales y, por tanto, las pendientes de las rectas siguen el módulo de Young del material.
En segundo lugar, si comprobamos los
resultados dentro del periodo elastoplástico
vemos que la plastificación se produce
a 240 MPa y comienza, de forma muy
coherente, por las fibras más alejadas del
eje neutro. Pero en el análisis teórico la
plastificación llega hasta fibras más próximas
al centro de la viga. Esta diferencia
con el método numérico se debe a que a
medida que nos vamos acercando al eje
neutro, empiezan a influir las tensiones
cortantes en el método numérico, aspecto
que no se ha tenido en cuenta en el método
teórico.
Por último, si nos centramos en las tensiones
residuales, que es el objetivo principal
de este artículo, podemos observar
que la tendencia de las gráficas es básicamente
la misma. En principio el hecho de
que la plastificación sea más profunda en
el análisis teórico que en el simulado hace
ver la primera de las diferencias entre ambos cálculos. Se observa que la tensión residual máxima, en el análisis teórico, varía entre los -60 MPa y los 60 MPa, mientras que en el simulado entre los -45MPa y los 45 MPa. A pesar de estas diferencias, las curvas tienen la misma tendencia y llega la tensión residual a las mismas zonas de la viga.
Las diferencias entre ambas gráficas se deben a que en la teoría clásica solo se ha trabajado con los esfuerzos de flexión con respecto al eje transversal, mientras que en simulación numérica, a pesar de que se ha buscado una sección lo suficientemente esbelta, siempre influyen en mayor o menor medida el resto de esfuerzos. Estas diferencias son más importantes a medida que nos acercamos más a la fibra neutra de la pieza, ya que es allí donde influyen otros esfuerzos.
Por otro lado, hay que indicar que en el proceso de estabilización para poder simular las tensiones residuales, la recuperación elástica (springback) hace que la residual final tenga pequeñas diferencias con la teórica, a pesar de que los diagramas elástico y elastoplástico presentan una mayor similitud. Realmente, el proceso de recuperación elástica consiste en analizar el sólido estáticamente durante un tiempo, y el grado de optimización de este tiempo influye decisivamente en su recuperación. Este segundo razonamiento apoya la teoría de la intervención de otros esfuerzos no previstos
en los estudios teóricos.
Conclusiones
El comportamiento mecánico de un
material refleja la relación entre la fuerza
aplicada y la respuesta del material. Normalmente,
las propiedades mecánicas de
los materiales se determinan en laboratorios,
en cuyos ensayos se intenta reflejar
las posibles condiciones de servicio
que tiene el propio material. Pero la naturaleza
de la carga, el tiempo de aplicación,
la temperatura, etc., pueden influir
en la formación de tensiones internas que
modifica la respuesta del material, convirtiéndose
en uno de los factores que
tener en cuenta.
Debido a la limitación de las técnicas
experimentales para medir las tensiones
internas, y la dificultad que tiene
la resolución de las ecuaciones no lineales
que rigen el comportamiento de los
materiales en el estado elastoplástico, se
hace necesario la utilización de técnicas
de simulación numérica por FEM que
puedan garantizar la respuesta de las
estructuras, especialmente en situaciones
comprometidas. Como puede observarse en el análisis teórico, según la teoría
clásica que rige la resistencia de materiales,
y la simulación numérica realizada
con ABAQUS, se hace intuir que el algoritmo
que emplea el software para simular
este proceso no lineal presenta una
aproximación muy buena.
Una vez que se ha realizado este estudio
teórico deberíamos realizar un estudio
experimental para validar los resultados
obtenidos. Normalmente, este
estudio experimental lo realizaríamos
mediante la técnica del agujero ciego
(blindhole).
Una vez que tenemos los resultados
teóricos y los experimentales, si estos
concuerdan con los obtenidos por FEM,
se podría validar el proceso de simulación
numérica. Este aspecto es muy
importante desde un punto de vista profesional,
ya que podríamos modificar las
características del material, las dimensiones,
la tipología de carga, lo que nos
permitiría mejorar el producto final sin
tener que realizar más ensayos experimentales
y, por tanto, reducir costes.
Por último, no quiero dejar de comentar
la importancia de estos métodos
numéricos para el desarrollo de productos
nuevos en los departamentos de
I+D+i en cualquier empresa, especialmente
en aquellas que están en el sector
de la ingeniería técnica industrial.
Bibliografía
Beer, De Wolf & Johnston (2001). Mecánica de Materiales
(3a edición). McGraw-Hill Interamericana, México,
ISBN 0-07-365935-5.
Boyce MC, Cao J, Karafillis AP, Taylor LM (1995). Numerical
Simulations of Sheet Metal Forming, Proceedings
of 2nd International Conference. NUMISHEET 93,
Isehara, Japan, Ed. A. Makinovchi, et al.
Nagtegaal JC, Taylor LM (1991). «Comparison of Implicit
and Explicit Finite Element Methods for Analysis of
Sheet Forming Problems.» VDI Berichte, No. 894.
Tang SC, Wang NM (1988). «Analysis of Bending Effects
in Sheet Forming Operations.» International Journal
for Numerical Methods in Engineering, vol. 25, pp.
253-267.






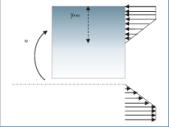

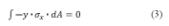



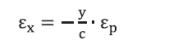

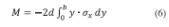

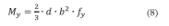
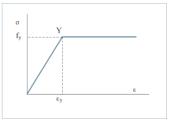 Figura 5. Estado elastoplástico perfecto de un acero dulce.
Figura 5. Estado elastoplástico perfecto de un acero dulce.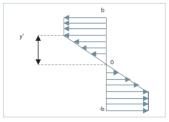 Figura 6. Estado elastoplástico en la sección transversal de una viga sometida a flexión.
Figura 6. Estado elastoplástico en la sección transversal de una viga sometida a flexión.