Simulación de filtros con el programa OrCAD
La utilización de este software de automatización del diseño de circuitos electrónicos aporta ventajas en la simulación de filtros electrónicos
Introducción
Un filtro eléctrico o filtro electrónico es un elemento que discrimina una determinada frecuencia o gama de frecuencias de una señal eléctrica que pasa a través de él, pudiendo modificar tanto su amplitud como su fase.
Los filtros se encuentran presentes en una gran cantidad de las aplicaciones electrónicas, lo que los hace esenciales. La construcción de un filtro implica el cumplimiento de múltiples compromisos, lo que lógicamente dificulta el cálculo de los valores de sus componentes retardando las soluciones y aumentando el tiempo de cálculo de sus parámetros. Precisamente el alto uso de los filtros despertó el interés por desarrollar herramientas que facilitaran el proceso de su diseño.
El programa informático OrCAD resuelve esta necesidad en gran medida, ya que permite la edición y simulación de circuitos eléctricos y electrónicos en general, y obviamente contempla estas tareas con circuitos de este tipo. Debido a que son circuitos muy utilizados, este software va un poco más lejos, ya que determinados tipos de filtros cuyas topologías son de sobra conocidas son incorporadas en sus componentes de simulación como un simple dispositivo en el que tan sólo será necesario indicar especificaciones propias del filtro que se desee emular, simplificando enormemente las tareas de dimensionado de circuitos y por supuesto disminuyendo las posibilidades de error inherentes a la edición y, en consecuencia, a la simulación.
Se expone en este texto, en primer lugar, la simulación de filtros típicos, mostrando las respuestas en frecuencia que ofrecen tras la correspondiente simulación. A continuación se hace más hincapié en los bloques de filtros que incorpora OrCAD con el cometido de facilitar las tareas de edición y simulación, explicando de una forma más detallada esta parte, ya que la primera es una posibilidad que contemplan muchos programas de simulación; sin embargo, la segunda es específica y que concede una serie de prerrogativas que se intentan dejar de manifiesto.
Simulación de filtros normales
Se comienza en un primer instante por mostrar filtros en su forma habitual, en la que se visualizan los componentes que conforman los mismos. Se comprueba en este primer apartado ya una pequeña diferencia entre dos tipos de filtros, un paso – bajo pasivo y el otro activo, desde el punto de vista de la simulación, en que es necesario más tiempo para que la simulación concluya en un caso que en el otro.
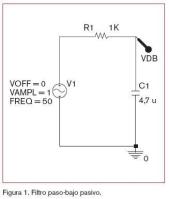
Filtro paso-bajo pasivo
El primero de los filtros es el que se muestra en la figura 1. Consiste en un filtro paso-bajo, en su topología más sencilla, para la cual tan sólo se emplea una resistencia y un condensador que será el encargado de atenuar las altas frecuencias a masa.
Se configura un perfil de simulación, para realizar un análisis ACSWEEP (barrido de frecuencias), cuyo rango del barrido de frecuencias sea suficiente para poder visualizar la respuesta del filtro adecuadamente. Se dispone además un marcador de tensión en decibelios, en el nudo de salida, para representar la respuesta del filtro ante la señal de entrada a las diferentes frecuencias a las que es sometido. En estas condiciones se tiene la respuesta representada en la figura 2, en donde se puede observar el rango de frecuencias definido para la simulación.
Se destaca además, al visualizar el fichero de salida generado tras concluir la simulación, que el tiempo empleado en llevar a cabo la simulación para este caso es de 0,18 segundos.
Filtro paso-bajo activo
Para este apartado se emplea el circuito de la figura 3, se trata de un filtro paso-bajo activo tipo Chebyshev de segundo orden. Obviamente, si el filtro fuese de mayor orden sería necesario un circuito de mayor complejidad. El hecho de que se haya usado este tipo de filtro es debido a que los dispositivos que se emplearán después que emulan los filtros, simulan a estos en concreto.
Para este caso, igual que para el anterior caso, se configura un perfil de simulación, para realizar un análisis ACSWEEP (barrido de frecuencias), cuyo rango del barrido de frecuencias sea suficiente para poder visualizar la respuesta del filtro adecuadamente. Se dispone también un marcador de tensión en decibelios, en el nudo de salida, para representar la respuesta del filtro. La respuesta para este caso es la que se muestra en la figura 4.
Se destaca ahora en este caso, al visualizar el fichero de salida genera-do tras concluir la simulación, que el tiempo empleado en llevar a cabo la simulación para este caso es de 0,43 segundos.
Bloques especiales para emular filtros
Alojados en la librería ABM.OLB, existen una serie de componentes que emulan filtros. Debido a que es muy frecuente la utilización de este tipo de circuitos y, para que cada vez que se necesite uno, no sea necesario editar el esquema entero, entonces este software ofrece una serie de bloques en el que sólo se necesitan indicar las especificaciones de la respuesta deseada de los circuitos que emulan. Otra ventaja significativa que ofrecen es que la simulación es mucho más rápida utilizando estos elementos que si se le hace al circuito que realice la misma función.
En concreto, estos bloques emulan filtros tipo CHEBYSHEV. Para que el programa identifique el filtro deseado, se le han de cumplimentar una serie de parámetros a los bloques. Por un lado, se tiene el rizado en la banda pasante, definido en los parámetros de los bloques como RIPPLE (en decibelios). Después, con conjuntos de tres propiedades, se define la atenuación, siendo necesario para ello indicar la frecuencia de corte, otra frecuencia de referencia posterior y la atenuación que se produce entre ellas en decibelios. En función de estas propiedades definidas, el programa escoge el polinomio del filtro para esas especificaciones.
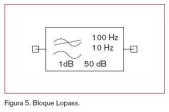
Bloque Lopass
Con este bloque se va a poder implementar un filtro paso-bajo; su forma es la que se muestra en la figura 5.
De las propiedades, para indicar las especificaciones requeridas en el filtro, se han de cumplimentar las siguientes:
FP. Frecuencia de corte.
FS. Frecuencia STOP de referencia.
RIPPLE. Rizado en la banda pasante en decibelios.
STOP. Atenuación en decibelios existente entre la frecuencia de corte y la frecuencia STOP de referencia.
Se ubican de forma gráfica en la respuesta frecuencial tipo paso-bajo de la figura 6 los diferentes parámetros comentados.
Las propiedades del componente se cumplimentan desde el cuadro de propiedades del elemento o directamente desde el esquema, pues todas ellas son accesibles desde el dispositivo.
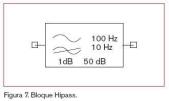
Bloque Hipass
Con este bloque se emulará un filtro paso alto. Su forma se muestra en la figura 7.
Las propiedades a cumplimentar en este caso para indicar el funcionamiento deseado son las mismas que las del componente anterior, teniendo en cuenta que es un filtro paso alto en lugar de un paso-bajo. En este caso, también son accesibles desde el componente.
Bloque Bandpass
Con este bloque se emulará un filtro paso banda. La forma que posee se muestra en la figura 8.
El funcionamiento deseado en este caso se configurará cumplimentando las siguientes propiedades:
F0. Referencia de la frecuencia de corte inferior situada previamente a ésta.
F1. Frecuencia de corte inferior.
F2. Frecuencia de corte superior.
F3. Referencia de la frecuencia de corte superior situada a continuación a ésta.
RIPPLE. Rizado en la banda de paso.
STOP. Atenuación entre las frecuencias de corte y las correspondientes referencias.
Se identifican también en este caso los diferentes parámetros en la respuesta frecuencial de un filtro tipo paso banda de la figura 9.
También en este caso existe la posibilidad de cumplimentarlas desde el cuadro de propiedades del elemento o directamente desde el esquema.
Bloque Bandrej
El filtro que se emula con este elemento es un tipo banda eliminada. La forma que posee se muestra en la figura 10.
Las propiedades para especificar el filtro son las mismas que las del componente Bandpass, teniendo en cuenta que es una banda eliminada en lugar de un paso banda, siendo de este modo las frecuencias de corte F0 y F3, y las de referencia F1 y F2. Al igual que en los casos anteriores, dichas propiedades son accesibles directamente desde el editor de esquemas.
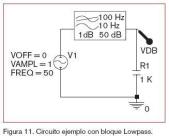
Ejemplo con un bloque Lowpass
En este apartado se muestra un ejemplo muy sencillo del empleo de estos bloques, en lugar de la implementación de un filtro con los componentes que requieren. Se hace con un bloque Lowpass, ya que al comienzo del trabajo se realizaron ejemplos con filtros paso-bajo. El circuito utilizado para este caso es el que se muestra en la figura 11.
Como se puede observar, el esquema es muy sencillo: en él existe una fuente de alimentación a la entrada del bloque, el bloque, configurado en este caso con los valores que el tiene por defecto, y a la salida de éste se dispone una resistencia que sería la carga a alimentar con la señal ya filtrada. A la salida del bloque Lowpass se pone un marcador de tensión en decibelios al igual que para los ejemplos que se realizaron al comienzo del documento.
Se configura un perfil de simulación, para realizar un análisis ACSWEEP, cuyo rango del barrido de frecuencias sea suficiente para poder visualizar la respuesta del filtro adecuadamente. La repuesta para este caso es la que se muestra en la figura 12
En este caso, al visualizar el fichero de salida generado tras concluir la simulación, se observa que el tiempo empleado en llevar a cabo la simulación es de 0,37 segundos.
Conclusiones
En este texto se ha expuesto fundamentalmente el funcionamiento de los bloques existentes en el software de OrCAD para emular los diferentes tipos de filtros que hay para la topología de los CHEBYSHEV.
Se resaltan varios aspectos a lo largo del artículo. El primero de ellos es la facilidad a la hora de su empleo, tanto desde el punto de vista de la configuración en la que son necesarios muy pocos los parámetros a cumplimentar para obtener un filtro con unas buenas especificaciones, como desde la facilidad en la edición de un circuito en la que se emplee un filtro, y de este modo sólo es necesario insertar un componente, cuando se ha visto antes que para implementar un filtro de orden dos del tipo que emulan, son necesarias cuatro resistencias, dos condensadores y un operacional. Si el orden del filtro necesario aumentase, el circuito electrónico se complicaría también.
Otro aspecto que se ha resaltado en cada ejemplo es el tiempo transcurrido en la simulación. Cuando se utiliza un bloque en lugar del filtro que emulan, el tiempo de simulación disminuye considerablemente. No ocurre lo mismo para el caso del filtro pasivo, pero es necesario tener en cuenta el filtrado obtenido de una manera y de otra, y por tanto tan sólo sería comparable con el filtro tipo CHEBYSHEV. A medida que se aumenta el orden del filtro, esta característica mejora en gran medida con la utilización de los bloques.
Bibliografía
Calvo Rolle, José Luis. Edición y simulación de circuitos con OrCAD. Editorial RA-MA. Octubre 2003.
Gómez Campomanes, José. Automática. Análisis y diseño de los sistemas automáticos de control. Tomos 1 y 2. Júcar. Madrid 1986.
Leira Rejas, Alberto José. Fundamentos de tecnología electrónica: teoría, problemas resueltos y simulaciones por ordenador. Editorial Copy Belén. 2001.
Katsuhiko Ogata. Ingeniería de Control Moderna. Ed. Prentice Hall Pearson Education. 2002.
Paul H. Lewis y Chang Yang. Sistemas de control en ingeniería. Prentice Hall, Inc., Madrid 1999.
RESUMEN
El presente artículo aborda la simulación de filtros con el programa informático OrCAD. Se comienza con la simulación de filtros normales, para, a continuación, pasar a ver cómo emplear los bloques existentes en el software OrCAD de simulación de circuitos eléctricos y electrónicos. Se intentan exponer las ventajas que supone la utilización de los mismos en la simulación electrónica, sobre todo, teniendo en cuenta que emulan un tipo de filtro muy concreto y enormemente utilizado. El interés de su empleo subyace en dos ventajas fundamentales. La primera consiste en la no necesidad de editar un filtro entero, con todos los dispositivos que requiere su implementación, cada vez que sea necesaria su utilización. La segunda corresponde a la velocidad de simulación, que será mucho más rápida empleando estos componentes, que no el circuito al que emulan, debido fundamentalmente a que es un simple dispositivo que funciona de acuerdo a unas especificaciones determinadas implementadas en el modelo que posee; sin embargo, un circuito de un filtro son muchos dispositivos, y cada uno con sus propias especificaciones.