Resolución de la cinemática de mecanismo ferroviario utilizando el cómputo paralelo sobre GPU
Resolution of the railway kinematics mechanism using parallel computing on GPU
Resumen
El uso de las tarjetas gráficas actuales para la resolución de problemas de ingeniería es un fenómeno creciente tanto en la industria como en la investigación. En este trabajo, los autores presentan las principales características que hacen atractivas las tarjetas gráficas para la resolución de problemas computacionales en la ingeniería. Además, se explican los pasos que componen el proceso de ejecución de un algoritmo típico en el procesador de la tarjeta gráfica. Con el objetivo de verificar la viabilidad de la tecnología, se plantea un modelo que soluciona el problema cinemático de un mecanismo ferroviario y se aplica esta tecnología para la resolución del modelo matemático. Este modelo se implementa de manera secuencial en el procesador del ordenador y de manera paralela en la tarjeta gráfica. El análisis de los tiempos de ejecución del modelo en distintas condiciones operativas permite determinar las fortalezas y debilidades de aplicar la nueva tecnología con respecto a los ordenadores convencionales.
Palabras clave
GPGPU, GPU, CUDA, computación paralela, simulación, mecanismo ferroviario.
Abstract
The use of current graphic cards for the resolution of engineering problems is a growing phenomenon in both industry and research. In this work, the authors present the main features that make graphic cards attractive for the resolution of computational problems in engineering. In addition, the steps for the execution of a typical algorithm in the graphic card processor are explained. In order to verify the viability of this technology, a model for solving the kinematics of a railway mechanical system is posed and this technology is applied for the resolution of the mathematical model. This model is implemented sequentially in the computer’s processor and in parallel way in the graphic card. The analysis of the execution times of the model in different operating conditions allows to determine the strengths and weaknesses of applying the new technology with respect to conventional computers.
Keywords
GPGPU, GPU, CUDA, parallel computing, simulation, railway mechanism.
Recibido / received: 21.04.2018. Aceptado / accepted: 21.05.2018.
Introducción
Tradicionalmente, las tarjetas gráficas y sus unidades de procesamiento, llamadas GPU por sus siglas en inglés (Graphic Processing Unit), se han utilizado para la generación de gráficos en videojuegos o simuladores y en tareas de renderizado de secuencias de animación. Sin embargo, los procesadores de las tarjetas gráficas o GPU presentan unas características que hacen muy atractiva su aplicación al cómputo de problemas con un gran número de operaciones y/o procesos iterativos. Del mismo modo que los procesadores de los ordenadores, llamados CPU por sus siglas en inglés (Central Processing Unit), la GPU está encapsulada en un único chip. La principal diferencia entre ambos chips es el número de procesadores y las tareas que desarrollan cada uno de ellos. Una CPU actual dispone habitualmente de 4 u 8 núcleos de proceso (Fig. 1), mientras que una GPU dispone de cientos o miles de núcleos de proceso. No obstante, los núcleos de la GPU realizan tareas más sencillas que los de la CPU. Mientras que los núcleos de la CPU se optimizan para ejecutar tareas de manera secuencial, los núcleos de la GPU se disponen con una arquitectura paralela que permite realizar varias
tareas a la vez. En la tabla 1 (Ghorpade
et al, 2012) se recogen las principales
ventajas de los chips, y se observa que
las características de la CPU se orientan
a la eficiencia de las tareas de los
sistemas operativos, mientras que la
GPU destaca en las operaciones en
coma flotante.
En el año 2006 se produce un punto
de inflexión en el desarrollo de las tarjetas gráficas: NVIDIA introduce una nueva arquitectura, denominada CUDA (Compute Unified Device Architecture), en sus GPU. Esta nueva arquitectura, junto con sus herramientas de programación y desarrollo (API, Application Programming Interface, y SDK, Software Development Kit) permite ejecutar toda clase de tareas en las tarjetas gráficas (Tasora, Negrut y Anitescu 2011). De esta forma, nace la computación de propósito general
sobre unidades de procesamiento
gráfico o GPGPU (por sus siglas
en inglés General-Purpose Computing
on Graphics Processing Units). Desde
entonces, tanto investigadores como
empresas de software han incorporado
esta tecnología en sus investigaciones
y productos comerciales (Ghorpade
et al, 2012).
En lo que respecta al campo de la
investigación, destacan los trabajos de
simulación de la dinámica de sistemas
multicuerpo y de partículas, con el
grupo de trabajo encabezado por los
profesores Dan Negrut y Alessandro
Tassora como uno de los más prolíficos
(Tasora y Anitescu, 2011; Tasora
et al, 2015; Negrut, Serban y Tasora,
2017; Hwu, 2011); el desarrollo
de nuevos algoritmos matemáticos
(Mawson y Revell, 2014; Ren y Chan,
2016); la reconstrucción de imágenes
médicas (García Blas et al, 2014; Després
y Jia, 2017); la simulación computacional
de fluidos (Sierakowski,
2016), etc. En el ámbito comercial,
numerosos programas de cálculo de
diversos ámbitos han implementado
esta tecnología. Entre ellos destacan
ANSYS, Abaqus, CST Studio Suite y
BRS Labs AISight for SCADA, en el
campo de la ingeniería, pero también
se aplica a las finanzas, la predicción
del clima, big data, etc. Incluso se
utilizan ampliamente para el minado
de criptomonedas como el bitcoin
(Taylor, 2017).
La principal ventaja de esta tecnología es la notable reducción de tiempo que se puede conseguir respecto a la tecnología tradicional (hasta 10 veces más rápido, dependiendo de la aplicación [Castonguay, 2012]). No menos importante es el bajo coste de esta tecnología: el precio de las GPU más avanzadas ronda los 8.000 €, pero una GPU de gama media o alta se puede adquirir por menos de 400 euros.
En este trabajo se exploran las capacidades de las GPU mediante la aplicación de la tecnología GPGPU al cómputo de la cinemática de un mecanismo de barras de utilidad en el sector ferroviario. Para ello se proponen varios modelos de análisis del mecanismo con el objetivo de evaluar las capacidades de la GPU. Además, los modelos se implementan en dos lenguajes de programación y se comparan los resultados obtenidos.
Computación en paralelo utilizando GPU
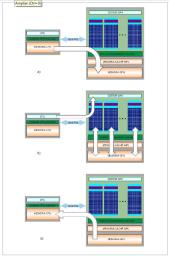
La generación de gráficos en los ordenadores actuales puede realizarse de dos formas: mediante una tarjeta gráfica integrada en la CPU (lo cual limita los recursos de la CPU), o mediante una tarjeta gráfica dedicada que cuenta con su correspondiente GPU (es el caso que nos concierne en este trabajo). Por tanto, la CPU y la GPU son dos elementos físicos distintos, cada uno con una memoria asociada, que se comunican mediante un bus (del tipo PCI Express actualmente). Con esta disposición, si se desea ejecutar tareas en la GPU y aprovechar sus capacidades de cálculo, el primer paso que hay que realizar es introducir los datos a través de la CPU y copiarlos posteriormente a la GPU. Este proceso se ilustra en la figura 2A. A continuación, se envían las instrucciones de ejecución al gestor de la GPU, que se encarga de distribuir y ejecutar las tareas entre los múltiples procesadores de la GPU (fig. 2b). El último paso consiste en copiar los resultados de la GPU a la CPU para poder trabajar con ellos (fig. 2c). El principal inconveniente de esta tecnología es, precisamente, la transferencia de datos entre las memorias de los dos chips, pues el bus PCI Express que los conecta es mucho más lento que los buses que conectan cada uno de los chips con sus respectivas memorias. Se trata, además, de un cuello de botella que no se puede evitar.
El proceso que se realiza con el software es muy similar, pues, habitualmente, un algoritmo GPGPU ejecuta parte del código en la CPU y parte en la GPU. Aplicando la nomenclatura de CUDA, cada una de las funciones que se ejecutan en la GPU recibe el nombre de kernel. Durante la ejecución de un kernel se lanzan varios hilos en paralelo que realizan la misma tarea con diferentes datos. No obstante, un kernel no llama a los hilos directamente, sino a una malla. Esta malla se compone de varios bloques que a su vez están formados por múltiples hilos. El número máximo y las características de estos elementos (malla, bloque e hilos) dependen de la GPU que se utilice y se deben tener en cuenta al escribir el código.
A partir de la versión 6 de CUDA, NVIDIA introdujo el concepto Unified Memory (UM), o memoria unificada. Este nuevo concepto simplifica la gestión de las memorias que debía realizar el programador al crear una ubicación común de memoria que es compartida por la CPU y la GPU. De esta forma, es suficiente con definir adecuadamente las variables necesarias una única vez, puesto que Unified Memory se encarga de asignar y transferir datos entre las memorias de la CPU y de la GPU (Harris, 2013).
Descripción del mecanismo y del modelo cinemático
El movimiento de lazo es una inestabilidad inherente al ferrocarril, por lo que controlarlo es un aspecto fundamental para garantizar la estabilidad de los vehículos ferroviarios y la comodidad de los pasajeros. En este trabajo se propone el dispositivo de la figura 3 como posible mecanismo para controlar el movimiento de lazo. Se compone de tres mecanismos fundamentales: uno de generación (basado en el mecanismo de Chebyshev y que comprende las barras 1, 2, 3 y 4), otro de pantógrafo (barras 5, 6, 7 y 8) y otro de refuerzo (formado por el resto de eslabones). Sus dimensiones se recogen en la tabla 2.
El mecanismo de refuerzo se une a los otros dos mecanismos mediante una junta de rotación situada en el punto B1. Además, la barra que une los puntos B y B1 dispone en uno de sus extremos de un elemento que se desplaza dentro de una deslizadera. Esta deslizadera se encuentra fijada al elemento de soporte del mecanismo (Bustos, Carbone et al, 2015; Bustos, Rubio et al, 2015).
Para garantizar que el mecanismo propuesto trabaja debidamente, es necesario efectuar análisis reiterativos sobre el mecanismo hasta obtener el funcionamiento deseado. Se aplicará la tecnología GPGPU al cálculo de la cinemática del mecanismo y se implementa los algoritmos de cálculo en C++ y en MATLAB. El análisis de los tiempos de computación necesarios para realizar los cálculos en am-bas plataformas permitirá detectar las fortalezas y debilidades de la computación paralela.
Modelo cinemático
El primer paso para la obtención de la cinemática del mecanismo es el planteamiento de las ecuaciones de cierre de las cadenas cinemáticas que componen el mecanismo. Tras resolver estas ecuaciones, se dispone de un conjunto de ecuaciones explícitas en función del ángulo de entrada (  2) (Bustos, Carbone et al, 2015). Tomando esto en cuenta, la posición angular de cualquier eslabón se puede escribir:
2) (Bustos, Carbone et al, 2015). Tomando esto en cuenta, la posición angular de cualquier eslabón se puede escribir:
Las coordenadas X e Y de los centros de masas (situados en el punto medio de cada barra) se pueden expresar fácilmente con respecto al ángulo de entrada:
Si el ángulo de entrada O2 está definido por una función temporal conocida, las ecuaciones anteriores se pueden escribir en función del tiempo y obtener las velocidades y aceleraciones mediante la primera y segunda derivadas.
De este modo, utilizando el método de Raven, se pueden plantear cuatro sistemas de ecuaciones (ecuaciones 3, 4, 5 y 6) para las cuatro cadenas cinemáticas que componen el mecanismo, de forma que el problema cinemático queda total-mente definido.
Donde O es el ángulo y r es la longitud de un eslabón j;
MB es la distancia entre los puntos M y B; y δ es el ángulo definido entre la deslizadera y el eslabón del mecanismo de refuerzo, en sentido antihoriario.
Tras resolver el sistema de ecuaciones correspondiente al mecanismo de Tchebychev, se obtienen los ángulos 4 y O, como funciones de, como muestran las ecuaciones 32 (7) y (8); aaux, baux y caux son variables auxiliares dependientes de O que se han introducido para reducir el tamaño de
2 la ecuación.
Este mismo proceso se aplica al resto de sistemas de ecuaciones, de tal forma que los ángulos O8 , O6 , O7 (obtenidos mediante una sencilla relación geométrica con O6), O9, O11, O10 y O se relacionan con el ángulo de entrada mediante las 12O2 expresiones de las ecuaciones (9)-(15). Como en el caso anterior, se han introducido los parámetros dependientes de f , a, b, a, b, y c con el fin de reducir el tamaño de las ecuaciones.
Una vez que se han calculado todos los ángulos, la obtención de las posiciones de los puntos característicos del mecanismo es trivial. Por último, tomando la primera derivada de esas ecuaciones se obtendrán las velocidades angulares (y, seguidamente, las velocidades lineales de los puntos), y tomando la segunda derivada, las aceleraciones. Por tanto, la cinemática del mecanismo queda totalmente definida.
Implementación del modelo cinemático
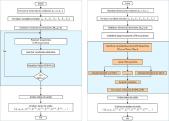
Para realizar el cálculo del modelo cinemático se desarrollan dos algoritmos, uno secuencial y otro paralelo, que se implementan sobre C++ y sobre MATLAB (en versiones R2013b y R2017b). El diagrama de flujo del algoritmo secuencial se muestra en la figura 4. El algoritmo comienza con la introducción de los datos de entrada (dimensiones de los eslabones, condiciones iniciales, condiciones de iteración y tiempo total de la simulación). Posteriormente, se calcula la cinemática del mecanismo para cada paso de tiempo. En la implementación en C++ esto se hace mediante un bucle. Sin embargo, en MATLAB se puede prescindir de este bucle si se aprovechan las capacidades de este lenguaje de programación y se utiliza la vectorización. En último lugar, se almacenan los resultados, y se pueden graficar los mismos para un análisis visual.
El algoritmo paralelo para el cálculo de la cinemática se implementa también con MATLAB y C++. En MATLAB, los dos algoritmos son bastante similares y únicamente se deben añadir unas pocas líneas de código requeridas para llevar a cabo la computación paralela.
Sin embargo, la implementación del algoritmo en CUDA C++ requiere más operaciones. A cambio, se tiene un control total sobre la gestión de la memoria y de los hilos de ejecución. En la versión C++ del algoritmo paralelo, el bucle del algoritmo secuencial se sustituye por n hilos de ejecución, tantos como pasos de tiempo que calcular, que se lanzarán y ejecutarán en paralelo, en la GPU.
El diagrama de flujo del algoritmo paralelo se muestra en la figura 5. Las primeras etapas son idénticas a las del algoritmo secuencial: introducción de datos de entrada, condiciones iniciales, etc. Es en el siguiente paso en el que comienzan las diferencias. En primer lugar, es necesario identificar las características de la GPU que establecen el número máximo de hilos paralelos que se pueden lanzar y cómo debe hacerse. Concretamente, se identifica el número máximo de hilos por bloque (NMthread), el número máximo de bloques (NMblock) y el tamaño máximo de la malla (NMgrid). Esencialmente, estos parámetros determinan cuántos hilos por bloque y cuántos bloques pueden ejecutarse en la GPU. A continuación, se asigna la memoria necesaria para las variables que se utilizarán y se ejecutan los hilos paralelos para calcular la cinemática. Los hilos se reparten en tantos bloques como sean necesarios para no sobrepasar el número máximo de hilos por bloque, de tal forma que no se excedan las capacidades de la GPU. Una vez realizados los cálculos, se sincronizan las memorias de la GPU y la CPU, se almacenan y se grafican los resultados.
Resultados
En este apartado se muestran los resultados de los tiempos de computación de los modelos presentados anterior-mente en diferentes condiciones. To-dos los experimentos se efectuaron en un PC con un procesador Intel Xeon E5410 a 2,33 GHz, 6 GB de memoria RAM y una tarjeta gráfica NVIDIA GeForce GTX 660 Ti. Se utilizaron los programas MATLAB en versiones R2013b y R2017b, y Visual Studio 2010 Professional con la Toolkit 6 de CUDA.
Se han realizado experimentos con 10 niveles de coste computacional, para cada algoritmo y plataforma, monitorizando su tiempo de ejecución. Para cada nivel de coste de computación se han realizado 20 experimentos, con el fin de tener suficientes muestras para el tratamiento estadístico de los datos. Debido al elevado tiempo de ejecución de los últimos niveles de cómputo bajo MATLAB con CUDA y a que la tendencia era clara, estos resultados no se han incluido.
Los tiempos de ejecución obtenidos en los experimentos del modelo cinemático se recogen en la tabla 3. La primera columna corresponde al nivel de cómputo y muestra el número de pasos de iteración computados en cada simulación. Las siguientes columnas muestran el tiempo medio de ejecución y el factor de aceleración, el cual resulta de dividir el tiempo medio de ejecución de cada nivel de computación y plataforma
entre el tiempo medio obtenido
en las simulaciones bajo CUDA C++.
Los datos de la tabla 3 solo contabilizan
el tiempo empleado en la resolución
de las ecuaciones; no tienen en
cuenta el tiempo requerido para asignar
memoria u otras variables.
La figura 6 muestra la evolución de
los tiempos medios de ejecución, con
ambos ejes en escala logarítmica. Se
observa que el mejor rendimiento se
obtiene usando CUDA C++. Los algoritmos
sobre C++ y MATLAB muestran
un desempeño similar para un
número bajo de iteraciones, y MATLAB
es más rápido que C++ para los
números de iteraciones más elevados.
No obstante, ambos son más lentos
que el código de CUDA C++. La combinación
de MATLAB con la GPU
resulta la más lenta de todas, a pesar
de seguir las recomendaciones del desarrollador
del programa y utilizar la
vectorización (MATLAB 2013). Durante
estos experimentos, también se
ha comprobado que la precisión doble
en coma flotante y, particularmente,
la existencia de sentencias de control
como if-end perjudican la ganancia de
tiempo en MATLAB CUDA.
Comparando los resultados de las
dos versiones de MATLAB se aprecia
un ligero incremento de la velocidad
de cálculo de la versión más reciente
del programa.
También es interesante representar
los factores de aceleración del cómputo
utilizando CUDA C++ respecto a
C++ y MATLAB, como se muestra en
la figura 7. En esencia, se representa
cuántas veces es más rápido el cálculo
utilizando CUDA C++ respecto a utilizar
C++ (en naranja) y MATLAB (en
azul y verde). En la figura 7 no se han
incluido los resultados obtenidos de las
simulaciones con MATLAB CUDA
(resultados desfavorables, como se comentó
anteriormente) por cuestiones
de claridad en la gráfica. Se aprecia
que CUDA C++ ejecuta las rutinas
hasta 90 veces más rápido que C++ y
hasta 40 veces más rápido que MATLAB.
También se observa que, a partir
de 2.500 iteraciones, MATLAB es más
rápido que C++.
En la figura 8 se representa la evolución
del tiempo de ejecución por
iteración de las seis implementaciones
llevadas a cabo. Se observa que el tiempo
por iteración en CUDA C++ se reduce
a medida que aumenta el número
de estas, hasta llegar a las 100.000. A
partir de aquí, se estabiliza en torno
a 1,4·10-4 ms por iteración. El tiempo
de cómputo por iteración para la implementación
en C++ es prácticamente
constante, con un valor de 0,01 ms/
iteración. Sin embargo, la versión de
MATLAB de la rutina sigue una ligera
pendiente descendente que comienza
en 0,02 ms/iteración y acaba en 0,005
ms/iteración. En lo referente al código
en MATLAB CUDA, el tiempo por
iteración presenta también una tendencia
descendente.
Conclusiones
En este trabajo se ha estudiado el coste computacional de la cinemática de un mecanismo ferroviario. Para ello se han empleado métodos de computación secuencial (utilizando solo la CPU) y en paralelo (mediante GPU). Los tiempos de ejecución necesarios para el cálculo de cada proceso se han analizado sobre cuatro plataformas distintas: C++, MATLAB, C++ con CUDA y MATLAB con CUDA, y con diferentes volúmenes del problema.
Los resultados del modelo cinemático del mecanismo ferroviario, consistente en cálculos puramente iterativos, prueban la eficiencia del GPGPU. Los menores tiempos de ejecución se obtienen con CUDA C++. Es la opción más recomendable cuanto mayor es el número de iteraciones que calcular, y se obtienen reducciones temporales de hasta 90 veces respecto a C++, de hasta 60 veces respecto a MATLAB R2013b y de hasta 40 veces respecto a MATLAB R2017b. Por el contrario, la implementación del GPGPU en MATLAB no arrojó los resultados esperados en ninguna de las dos versiones de MATLAB probadas, siendo la implementación más lenta de todas.
La comparación entre las dos versiones de MATLAB (R2013b y R2017b) muestra un ligero aumento del rendimiento en la edición más nueva del programa, de modo que se reducen los tiempos de cálculo tanto sobre la CPU como utilizando la GPU.
Agradecimientos
Los autores desean agradecer el apoyo brindado por el Gobierno español para la financiación de este trabajo a través del proyecto competitivo MAQ-STATUS DPI2015-69325-C2-1-R.
Bibliografía
Bustos, A., Carbone, G., Rubio, H., Ceccarelli, M. Y García Prada, J.C., 2015. Sensitivity analysis on MIMBOT biped robot through parallel computing. En: J.M. FONT-LLAGUNES (ed.), ECCOMAS Thematic Conference on Multibody Dynamics 2015: Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics 2015. Barcelona: International Center for Numerical Methods in Engineering (CIMNE), pp. 15041515. ISBN 978-84-944244-0-3.
Bustos, A., Rubio, H., García Prada, J.C. Y Meneses, J., 2015. The Evolution of the Computing Time in the simulation of Mimbot-Biped Robot using Parallel Algorithms. Proceedings of the 14th IFToMM World Congress. Taipei, Taiwan: s.n., pp. 347-354. ISBN 978-986-04-6098-8.
Castonguay, P., 2012. Accelerating CFP simulations with GPUs. CLUMEQ: NVIDIA CUDA/GPU workshop [en línea]. Montreal, Canadá. [Consulta: 7 febrero 2018]. Disponible en: http://www.hpc. mcgill.ca/downloads/intro_cuda_gpu/2012-1245/ClumeqCastonguay.pdf.
Després, P. y JIA, X., 2017. A review of GPU-based medical image reconstruction. Physica Medica, vol. 42, pp. 76-92. ISSN 11201797. DOI 10.1016/j.ejmp.2017.07.024.
Garcia Blas, J., Abella, M., Isaila, F., Carretero, J. y Desco, M., 2014. Surfing the optimization space of a multiple-GPU parallel implementation of a X-ray tomography reconstruction algorithm. Journal of Systems and Software, vol. 95, pp. 166-175. ISSN 01641212. DOI 10.1016/j. jss.2014.03.083.
Ghorpade, J., Parande, J., Kulkarni, M. y Bawaskar, A., 2012. GPGPU Processing in CUDA Architecture. Advanced Computing: An International Journal, vol. 3, no. 1, pp. 105-120. ISSN 2229726X. DOI 10.5121/acij.2012.3109.
Harris, M., 2013. Unified Memory in CUDA 6. NVIDIA Developer Blog [en línea]. [Consulta: 7 febrero 2018]. Disponible en: https://devblogs. nvidia.com/unified-memory-in-cuda-6/.
Hwu, W.W., 2011. GPU computing gems: Jade edition. San Francisco, Cal.: Morgan Kaufmann. ISBN 978-0-12-385963-1.
Matlab, 2013. Measure and Improve GPU Performance. MATLAB® R2013b help. 2013. S.l.: s.n.
Mawson, M.J. y Revell, A.J., 2014. Memory transfer optimization for a lattice Boltzmann solver on Kepler architecture nVidia GPUs. Computer Physics Communications, vol. 185, no. 10, pp. 2566-2574. ISSN 0010-4655. DOI 10.1016/j. cpc.2014.06.003.
Negrut, D., Serban, R. y Tasora, A., 2017. Posing Multibody Dynamics With Friction and Contact as a Differential Complementarity Problem. Journal of Computational and Nonlinear Dynamics, vol. 13, no. 1, pp. 014503-014509. ISSN 15551415. DOI 10.1115/1.4037415.
Ren, Q. y Chan, C.L., 2016. Numerical study of double-diffusive convection in a vertical cavity with Soret and Dufour effects by lattice Boltzmann method on GPU. International Journal of Heat and Mass Transfer, vol. 93, pp. 538-553. ISSN 00179310. DOI 10.1016/j.ijheatmasstransfer.2015.10.031.
Sierakowski, A.J., 2016. GPU-centric resolved-particle disperse two-phase flow simulation using the Physalis method. Computer Physics Communications, vol. 207, pp. 24-34. ISSN 00104655. DOI 10.1016/j.cpc.2016.05.006.
Tasora, A. y Anitescu, M., 2011. A matrix-free cone complementarity approach for solving large-scale, nonsmooth, rigid body dynamics. Computer Methods in Applied Mechanics and Engineering, vol. 200, no. 5-8, pp. 439-453. ISSN 00457825. DOI 10.1016/j.cma.2010.06.030.
Tasora, A., Negrut, D. y Anitescu, M., 2011. GPU-Based Parallel Computing for the Simulation of Complex Multibody Systems with Unilateral and Bilateral Constraints: An Overview. En: K. ARCZEWSKI, W. BLAJER, J. FRACZEK y M. WOJTYRA (eds.), Multibody Dynamics [en línea]. Dordrecht: Springer Netherlands, Computational Methods in Applied Sciences, pp. 283-307. [Consulta: 7 febrero 2018]. ISBN 978-90-4819970-9. Disponible en: https://link.springer.com/ chapter/10.1007/978-90-481-9971-6_14.
Tasora, A., Serban, R., Mazhar, H., Pazouki, A., Melanz, D., Fleischmann, J., Taylor, M., Sugiyama, H. Y Negrut, D., 2015. Chrono: An open source multi-physics dynamics engine. High Performance Computing in Science and Engineering [en línea]. Soláň, Czech Republic: Springer, Cham, pp. 19–49. ISBN 978-3-31940360-1. DOI 10.1007/978-3-319-403618_2. Disponible en: https://link.springer.com/ chapter/10.1007/978-3-319-40361-8_2.
Taylor, M.B., 2017. The Evolution of Bitcoin Hardware. Computer, vol. 50, no. 9, pp. 58-66. ISSN 00189162. DOI 10.1109/MC.2017.3571056.










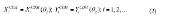 >BR>
>BR>