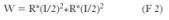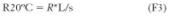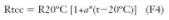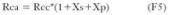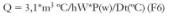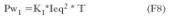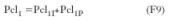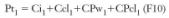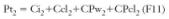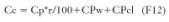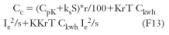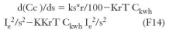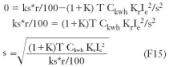Rentabilidad de las instalaciones con embarrados de baja tensión
El artículo revisa los parámetros que determinan el equilibrio entre el coste de la instalación el ahorro energético en transmisiones de energía eléctrica de baja tensión, especialmente en procesos industriales en los que se requieran grandes intensidades
En instalaciones industriales donde el mismo proceso requiera unas grandes intensidades éstas están sujetas a unas pérdidas que básicamente están condicionadas por dos parámetros:
• La resistencia eléctrica del propio material (prácticamente constante).
• El propio flujo eléctrico (intensidad).
El producto de la primera por el cuadrado de la segunda nos determina las pérdidas que se generan en forma de calor:
W la potencia en vatios.
R resistencia en ohmios.
I la intensidad en amperios.
Generalmente, los elementos empleados como conductores son el cobre (Cu), y puntualmente, el aluminio (Al), dispuestos en barras según la intensidad a transmitir. Aunque también existen actualmente en el mercado fabricantes que ofrecen el producto en conductores estándar (blindos-barra), que se adaptan prácticamente a todas las necesidades, dando al conductor una protección adecuada además de facilitar su instalación.
En una instalación determinada adecuada a la intensidad I necesaria, nos aparece el parámetro R (resistencia de la instalación).
Para este caso, nuestras pérdidas energéticas serían. WR*I2. ¿Qué pasaría si, doblando nuestra inversión, instaláramos dos conductores en lugar de uno? La intensidad se dividiría entre los dos conductores y tendríamos las pérdidas siguientes:
En este caso, las pérdidas se dividen por la mitad.
La instalación más rentable sería la que lograse equilibrar los costes de instalación y el ahorro energético.
Pérdidas por efecto joule
En las transmisiones de energía eléctrica a baja tensión, las pérdidas principales son debidas directamente al material empleado.
Se puede hacer una distinción significativa dependiendo de si es corriente continua o alterna.
Para la corriente continua, y a 20º C, la resistencia se expresa por:
Siendo:
R resistencia del material en ?*mm2/km
L longitud del conductor en Km
s sección efectiva en mm2
Siendo R para el Cu comercial igual a 17,6 ?*mm2/km. y para el Al, 28,6 ?*mm2/km.
Otro factor a tener en cuenta son las variaciones de temperatura, las cuales afectan sensiblemente la resistencia según:
Donde t es la temperatura y a es igual a 0,0039 para el Cu y 0,0040 para el Al.
Para el caso de corriente alterna, la resistencia sería:
Siendo:
Xs incremento de la resistencia debido al efecto Skin.
Xp incremento de la resistencia debido al efecto proximidad.
En los conductores con envolvente metálica, pantalla o armadura, se originan unas corrientes parásitas que gene-ran unas pérdidas adicionales de escasa influencia.
Coste por eliminación de pérdidas energéticas en forma de calor
En nuestras instalaciones (sala eléctrica, centros de distribución, etc.) normalmente nos vemos en la necesidad de eliminar el calor que se genera, que más que molesto para la propia estancia, resulta perjudicial para los equipos instalados.
Veamos de qué forma se puede compensar ese calor:
Existen en la práctica tres formas básicas de eliminación de la energía calorífica (refrigeración).
• Mediante ventilación natural. Se realiza instalando las rejillas de ventilación necesarias, y así se generará una circulación natural del aire mediante convención.
• Mediante ventilación forzada, es decir, instalando ventiladores o extractores que regeneren aire suficiente. Para este caso, el caudal de aire necesario sería:
Siendo:
Q caudal en m3/h
P potencia a disipar en w
Dt diferencia de temperatura en ºC (57ºC)
Aplicando la fórmula F6 para un kw obtenemos los siguientes resultados (según se tome Dt igual a 5ºC o a 7ºC), que serían: 620 m3/h a 443 m3/h.
Según las distintas formas constructivas de los ventiladores, el consumo necesario por m3/h de aire, varía aproximadamente entre 0,078 w por m3/h y 0,034 w por m3/h, lo que nos hace tener un consumo de ventilación por kw a disipar que varía entre 48 w a 15 w por kw.
• Mediante equipos de climatización. Este sistema puede ser de distintas variedades según fabricante o filosofía de instalación (bombas de calor, condensadores por aire, etc.). En cualquiera de los casos, el equipo a instalar precisa de un consumo de energía para su funcionamiento.
Dependiendo del sistema empleado o incluso del fabricante, la necesidad energética para compensar un kw varía de 0,48 a 0,55 kw.
Por consiguiente, en una instalación donde tengamos pérdidas en forma de calor, si no queremos que nos aumente la temperatura del local, debemos sumar un coste energético adicional para compensar estas pérdidas, ya sea mediante climatización o ventilación forzada.
Cálculo de la amortización anual para una inversión
En la realización de cualquier instalación, ésta nos va a suponer unos costes de inversión que, en función de los años previstos de amortización, se traducen en unos costes anuales. La determinación del coste anual de amortización viene determinado por la siguiente expresión:
Siendo:
Cp capital a amortizar
r (p*qn)/(qn1)
q (p/100)1
p interés anual
n años de amortización de nuestra instalación.
Hay que tener en cuenta, que los años de amortización previstos siempre han de ser inferiores a los años de vida de nuestra instalación.
Cálculo de la instalación más rentable
Supongamos un hipotético proceso industrial donde se precisen grandes intensidades, para lo cual prevemos una instalación a base de embarrados o blindosbarra como medio de transporte de la energía eléctrica. Una vez resuelto técnicamente el proyecto de instalación, nos aparecen unos costes, que en función de los años de amortización previstos, y según la expresión F7 serían:
Ci1 coste de la instalación propiamente dicha expresado en coste anual de amortización.
Ccl1 coste de la instalación de climatización expresado en coste anual de amortización (bien sea por ventilación o por climatización).
A esta instalación, hay que añadir unos costes adicionales anuales debidos a:
Pérdidas energéticas por rendimiento de la instalación Pw1 (pérdidas energéticas anuales) y Pcl1 (perdidas energéticas por consumo de los equipos de climatización, el consumo anual de los equipos).
Si multiplicamos las expresiones anteriores por el coste del kwh obtendremos:
CPw1 coste de las pérdidas energéticas en un año.
CPcl1 coste de los consumos de equipos de climatización en un año.
Las pérdidas energéticas por rendimiento de la instalación Pw1 dependen de varios factores:
Siendo:
K1 la constante propia de la instalación. Es la propia resistencia de los conductores.
Ieq la intensidad térmica equivalente consumida. Depende directamente del factor de servicio de la instalación.
T tiempo de trabajo de la instalación.
Los consumos energéticos de los equipos de climatización vienen determinados por dos sumandos:
Siendo:
Pcl1P el consumo energético de los equipos de climatización debido a las pérdidas energéticas Pw1.
Pcl1I el consumo energético de los equipos de climatización del resto de la instalación.
Los consumos energéticos Pcl1P son especialmente importantes cuando se opta por un sistema de climatización, sin embargo, no son tan significativos para un sistema de ventilación.
Por consiguiente, podríamos resumir el coste anual de amortización de nuestra instalación en la siguiente expresión.
Supongamos la resolución del problema anterior con un incremento de embarrados. Tendríamos la siguiente expresión:
En este caso, aparentemente, se tratade una instalación de coste superior:
Ci2 será superior a Ci1.
CPw2 será inferior a CPw1 según la expresión F8.
CPcl2 será inferior a CPcl1 según la expresión F9.
Ccl2 será igual o inferior a Ccl1.
Por lo tanto, tendríamos para el primer caso unos costes inferiores en instalación, pero unos costes de pérdidas y consumos de climatización anuales superiores al segundo caso.
Como ejemplo práctico, supongamos dos instalaciones, las dos válidas técnicamente, pero con distintos costes de partida:
– Primera instalación
Coste de instalación 600.000 €.
Coste de equipos de climatización 20.000 €.
Coste anual por pérdidas 60.000 €.
Coste anual por consumos de climatización 30.000 €.
• Coste total de la inversión 620.000 €.
• Coste anual por pérdidas y consumos 90.000 €.
– Segunda instalación
Coste de instalación 900.000 €.
Coste de equipos de climatización 20.000 €.
Coste anual por pérdidas 30.000 €.
Coste anual por consumos de climatización 20.500 €.
• Coste total de la inversión 920.000 €.
• Coste anual por pérdidas y consumos 50.500 €.
Partiendo de las dos instalaciones, y utilizando la expresión F7 tendremos un coste total de amortización anual que sería:
Cc1 Cp1*r/100CPw1CPcl1
para nuestra primera instalación, siendo Cp1 el coste de la inversión en instalación más el coste de los equipos de climatización.
Cc2 Cp2*r/100CPw2CPcl2
para nuestra segunda instalación, siendo Cp2 el coste de la inversión en instalación mas el coste de los equipos de climatización. Representando ambas funciones y partiendo de un interés anual p del 7% y de una variación de los años de amortización n de 5 a 20 años, obtenemos las curvas del gráfico Nº1 donde se puede apreciar que el coste de amortización anual es inferior para la segunda instalación a partir de los once primeros años.
Por consiguiente, nuestra segunda instalación resulta más rentable si los años de amortización estimados son superiores a once.
Determinación de la sección más rentable
En el ejemplo anterior, se pudo comprobar cual de las dos instalaciones era más rentable partiendo de una estimación de interés anual. El problema que se nos plantea resulta más complejo, ya que se trata de determinar la instalación más rentable partiendo de unas necesidades iniciales y de unos años de previsión de amortización.
Planteando la ecuación:
De donde:
Cc = coste de amortización a determinar.
Cp 0 coste de la instalación, que se compone de dos sumandos: CpK, que corresponde a los costes fijos de la instalación y Cps, que corresponde a los costes dependientes de la sección de los embarrados. Esto se puede resumir en la expresión Cps = ksS.
r depende del interés p estimado y de los años de amortización previstos.
CPw depende de la sección estimada s (resistencia eléctrica), de la intensidad térmica Ie y de una constante que depende del material empleado como conductor Kr, así como del tiempo de trabajo T y del coste estimado del kwh Ckwh. Si resumimos la expresión, tendremos: CPw = KrTCkwh Ie 2/s
CPcl = depende en parte de CPw multiplicado por una constante K de valor inferior a 1.
Por consiguiente, podemos replantear la ecuación de la siguiente manera:
Cc nos da una función f(s) que depende de la sección s.
La representación de esta función para unos años de amortización n = 5 y un interés p = 7% es la correspondiente al gráfico número 2. Para varios años de amortización podemos consultar el gráfico número 3.
Si queremos determinar el coste mínimo, tenemos que realizar la derivada primera de F13 en función de s y posteriormente, igualarla a cero. Despejando s de la función resultante, obtendremos la sección más rentable.
Igualando a cero la derivada, obtendremos el mínimo.
La sección determinada puede no corresponder con ninguno de los valores estándar existentes en el mercado. Si se diera el caso, deberíamos optar por el más aproximado.
Conclusión
Aunque este estudio está planteado para instalaciones con embarrados, nos puede surgir el mismo problema (determinar el coste más rentable) en instalaciones de potencia con cables de baja tensión o, yendo más allá, en cualquier tipo de instalación donde exista una transmisión de energía sometida a unas pérdidas que dependen de la propia configuración del medio para transportar el fluido.
Bibliografía
Siemens. Power Engineering Guide. Transmission and Distribution.
Llorente Antón, M. Cables Eléctricos Aislados. Descripción y aplicación práctica
Soler y Palau. Catalogo comercial.
Moeller. Canalizaciones eléctricas prefabricadas CK, CS. Catálogo comercial.
Roca & York. Aire acondicionado. Catalogo comercial.