Pérdida de carga y energía en impulsiones de fango deshidratado: análisis como fluido no newtoniano
Pressure and energy loss in dewatering sludge drives: analysis as a non-newtonian fluid
José García Cascallana (1)
Resumen
El comportamiento reológico de los fangos deshidratados es similar al de un fluido seudoplástico o adelgazante de tipo no newtoniano, y se puede considerar que sigue el modelo de Herschel-Bulkley. De esta forma, y una vez superada la tensión umbral, la derivada del esfuerzo cortante con respecto a la velocidad de deformación disminuye de forma no lineal al aumentar la velocidad de deformación, mientras que la viscosidad dinámica aparente disminuye. Este comportamiento es diferente al de los plásticos de Bingham, en los que dicha derivada se mantiene constante y, cuando la velocidad de deformación tiende a infinito, la viscosidad dinámica aparente coincide con la de Newton. El cálculo teórico de la pérdida de carga para este tipo de fluidos se ha realizado en régimen laminar a velocidades mucho menores que la crítica, donde el factor de fricción es inversamente proporcional al número de Reynolds de acuerdo con la ecuación de Poiseuille.
Palabras clave: Reología, viscosidad, polielectrolito, biosólidos, centrados.
Abstract
The rheological behaviour of the dewatered sludge is similar to that of a non-Newtonian pseudoplastic or thinning fluid, and can be considered to follow the Herschel-Bulkley model. Thus, once the threshold stress is exceeded, the derivative of the shear stress with respect to the strain rate decreases non-linearly as the strain rate increases, while the apparent dynamic viscosity decreases. This behaviour is different from that of Bingham plastics, in which this derivative remains constant and, when the strain rate tends to infinity, the apparent dynamic viscosity coincides with the Newtonian viscosity. The theoretical calculation of the head loss for this type of fluid has been carried out in the laminar regime at speeds much lower than the critical speed, where the friction factor is inversely proportional to the Reynolds number in accordance with Poiseuille’s equation.
Keywords: Rheology, viscosity, polyelectrolyte, biosolids, centrates.
Recibido / received: 03/11/2022. Aceptado / accepted: 15/02/2023.
(1) Ingeniero técnico industrial por la Universidad de León, ingeniero industrial por la UNED y doctor por la Universidad de León.
Autor para correspondencia (corresponding author): José García Cascallana; e-mail: jgc0504@yahoo.es
1. Introducción
La tensión cortante τ (N/m2) experimentada por un fluido al circular por un conducto se puede representar mediante la ecuación (1) que constituye la Ley de Newton de la viscosidad.
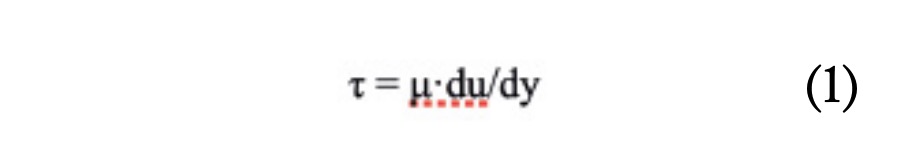En ella, μ es la viscosidad dinámica (Pa·s) y du/dy la velocidad de deformación por unidad de longitud (s-1).
Se denominan fluidos newtonianos (N) aquellos que presentan una relación lineal entre el esfuerzo cortante producido y la velocidad de deformación aplicada, cumpliendo con la Ley de Newton de la viscosidad (Bergadá-Grañó, 2012). Los fluidos N son los más sencillos de analizar y se caracterizan por la propiedad de que el gradiente de velocidad de deformación en un punto es proporcional al esfuerzo cortante (Levenspiel, 2022). Son fluidos no newtonianos (NN) aquellos que no cumplen la Ley de Newton de la viscosidad. La viscosidad de un fluido NN no existe como tal, ya que depende del valor que tenga en cada momento el esfuerzo cortante y, por tanto, es variable. El parámetro η se denomina viscosidad aparente (Pa·s), pero no solo varía con la temperatura, sólidos totales (ST, %), etc., como lo hace μ, sino también con τ (Navarro et al., 2007).
La diferencia básica entre el comportamiento de los fluidos N y NN es la longitud de la molécula, de forma que aquellos fluidos con moléculas de pequeño tamaño (agua, vapor de agua, todos los gases, etc.) presentan un comportamiento N en contraposición con aquellos (fangos, emulsiones, pinturas, etc.) que poseen moléculas de mayor tamaño y se comportan como fluidos NN (Navarro et al., 2007; Levenspiel, 2022). Los fluidos N son aquellos en los que la viscosidad es inherente a la naturaleza fisicoquímica de los mismos y, por tanto, independiente del esfuerzo cortante aplicado. Otra diferencia importante entre los fluidos N y NN se puede visualizar mediante el análisis de las ecuaciones (2) y (3) (Martín et al., 2011).
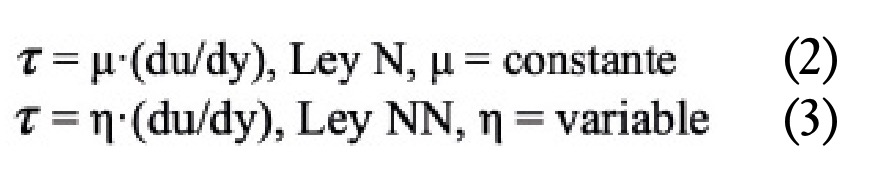La reología es definida en el Diccionario de la lengua española como, “el estudio de los principios físicos que regulan el movimiento de los fluidos”. La reología de un fango varía sensiblemente de una muestra a otra en función de los procesos de tratamiento realizados (Haldenwang et al., 2012), y es la ciencia que describe la deformación de los fluidos bajo la influencia de tensiones tangenciales (Seyssiecq et al., 2003). Las variables que influyen en la viscosidad dinámica son:
1. ST: aumenta al incrementarse ST. Se han descrito dos tipos de modelos matemáticos para considerar el efecto de ST en la viscosidad según la ecuación (4), modelo potencial y la ecuación (5), exponencial.
donde K1, K2, A1 y A2 son constantes.
2. Temperatura: disminuye al aumentar la temperatura. Varias fórmulas permiten evaluar la variación de la viscosidad de un fluido al cambiar la temperatura, y la ecuación (6) de Arrhenius es la más utilizada:
donde T es la temperatura absoluta (K), A y B constantes.
3. Presión: su efecto se ignora en el cálculo de la viscosidad (Panchi Guanoluisa, 2013). Hay varios modelos reológicos de los fluidos NN: ecuación (7), Sisko; ecuación (8), Careau; ecuación (9), Cross; ecuación (10), Bingham; ecuación (11), Ostwald (potencial), y ecuación (12), Herschel-Bulkley.
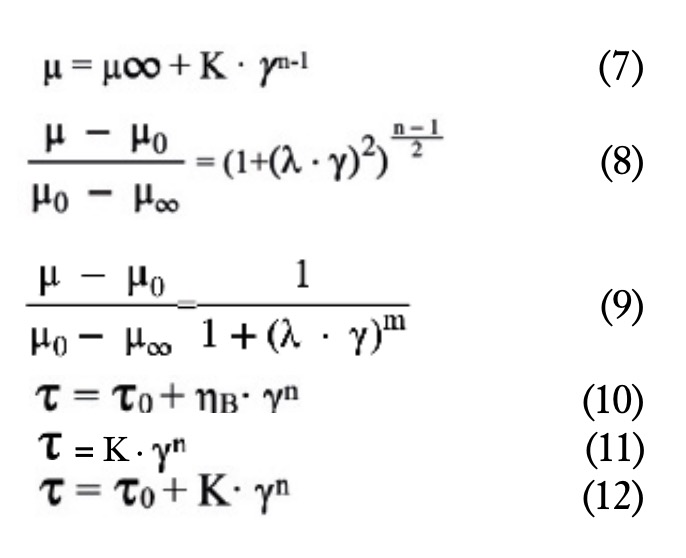donde μ∞ es la viscosidad aparente en el límite (Pa·s); K, el índice de consistencia (Pa·sn); γ, la velocidad de deformación (s-1); n, el índice de flujo; μο, la viscosidad aparente de cizalladura inicial (Pa·s); λ, la constante de tiempo (s); m, la constante de velocidad; το, la tensión umbral (Pa), y ηΒ, la viscosidad límite de alta cizalladura (Pa·s) (Hong et al., 2017). Los fluidos NN se pueden clasificar en: a. Fluidos independientes del tiempo: Velocidad de cizalladura= función de τ únicamente (García Villegas 2008). La figura 1a muestra el valor de τ y la figura 1b el de η, ambos en función de para distintos tipos de fluidos NN.
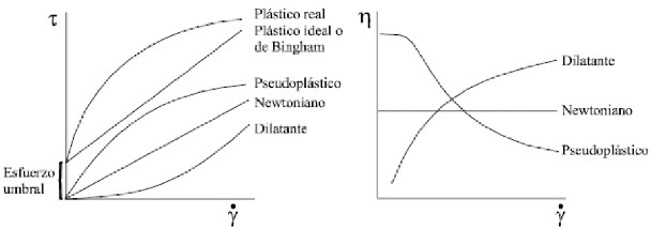
Los fluidos NN de este tipo pueden ser:
1. Plásticos reales o de Herschel-Bulkley: se comportan como sólidos elásticos, almacenando cierta cantidad de energía cuando son sometidos a esfuerzos por debajo de cierto valor umbral το, mientras que con un esfuerzo superior se deforman continuamente como un fluido, y el esfuerzo es una función no lineal de la velocidad de deformación. El índice de flujo es n < 1. Ejemplos típicos son: mahonesa, mermelada, arena de playa mojada, etc.
2. Plásticos ideales o de Bingham: requieren el desarrollo de un nivel significativo de tensión umbral το antes de empezar a fluir y la tensión cortante varía de forma proporcional con la velocidad de deformación, siendo n = 1. Cuando γ tiende a ∞, entonces ηB = µ. Algunos ejemplos son: chocolate, salsa de tomate, pasta de dientes, etc.
3. Seudoplásticos o adelgazantes: reducen su viscosidad dinámica aparente al aumentar la velocidad de deformación. Muchos materiales muestran este tipo de comportamiento en mayor o menor grado y es el comportamiento más común, con n < 1. Ejemplos de ellos son el plasma sanguíneo, la arcilla (Navarro et al., 2007), la pulpa de papel y la pintura (Levenspiel, 2022).
4. Dilatantes: aumentan su viscosidad dinámica aparente al ser incrementada la velocidad de deformación, causada por reorganizaciones dentro de su microestructura interna, donde n >1. Estos fluidos son poco numerosos: fécula de maíz en etilenglicol, almidón en agua etc. (Navarro et al., 2007), arenas movedizas y algunas emulsiones de arena (Ramiro Betancourt-Grajales, 2022).
b) Fluidos dependientes del tiempo:
Son fluidos cuyo comportamiento en un momento determinado está influenciado por lo que le haya ocurrido en el pasado reciente. Por ejemplo, la salsa de tomate que ha estado en reposo durante un rato no verterá. Sin embargo, recientemente agitada verterá fácilmente. Estos fluidos parece que tienen una memoria que se desvanece con el tiempo. Velocidad de cizalladura = función de τ según su historia pasada (Gardea-Villegas, 2007).
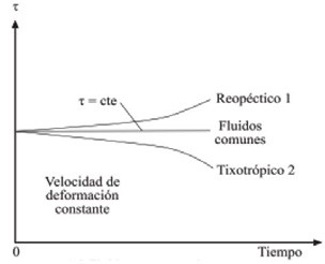
La figura 2 muestra la representación de la variación de τ frente al tiempo para tres tipos de fluidos, con γ = constante (Bergadá-Grañó, 2012).
Estos tipos de fluidos NN son los siguientes:
- Tixotrópicos: disminución reversible del esfuerzo cortante con el tiempo cuando γ es constante, por ejemplo: manteca, pintura y tinta (Navarro et al., 2007).
- Reopécticos: aumento reversible del esfuerzo cortante con el tiempo cuando γ es constante (Navarro et al., 2007; Ramiro Betancourt-Grajales, 2022).
c) Viscoelásticos: Exhiben una recuperación elástica de las deformaciones que se presentan durante el flujo y muestran propiedades viscosas y elásticas (Navarro et al., 2007). El diagrama τ frente a γ solo indica parte de la historia. Los fluidos NN dependientes del tiempo y los NN viscoelásticos no tienen una curva única de τ frente a γ (Levenspiel, 2022).
2. Objetivos
El objetivo de este artículo ha sido realizar el cálculo teórico de la pérdida de carga y energía asociadas a la impulsión de fangos deshidratados a partir de datos referenciados de viscosidad dinámica y aplicación de las ecuaciones clásicas de la mecánica de fluidos para flujo laminar. Estos resultados han sido comparados con valores reales obtenidos durante la operación de la EDAR de Burgos en el mes de marzo del año 2016 con objeto de poder establecer la viabilidad del procedimiento matemático adoptado durante el proceso de cálculo. Se ha desarrollado un análisis de sensibilidad de la impulsión para estudiar el comportamiento del flujo de fango y la variación de diversos factores operacionales de las bombas de impulsión. Finalmente, se ha calculado el diámetro económico de la impulsión.
3. Metodología
3.1. Descripción del escenario
La impulsión de fangos deshidratados objeto de análisis ha sido la existente en la EDAR de Burgos. La capacidad de tratamiento de aguas residuales en el año 2016 era de 118.000 m3/día y 833.000 habitantes equivalentes (EDAR, 2022).
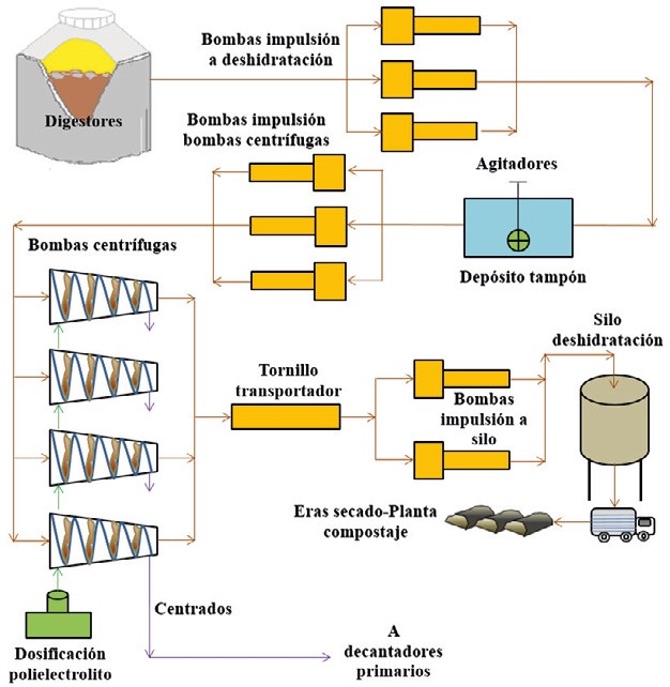
La figura 3 representa el diagrama de operación del bloque deshidratación de fangos. Con objetivo de regular convenientemente el flujo de fango digerido de entrada, se dispone de un depósito tampón desde el cual unas bombas de tornillo impulsan el fango a las bombas centrífugas en las que se añade una solución de polielectrolito y agua. El fango una vez deshidratado es enviado al silo de fangos por medio de un tornillo transportador y dos bombas de tornillo helicoidal. Los centrados originados son enviados a los decantadores primarios por gravedad, con objeto de ser recirculados nuevamente al proceso.
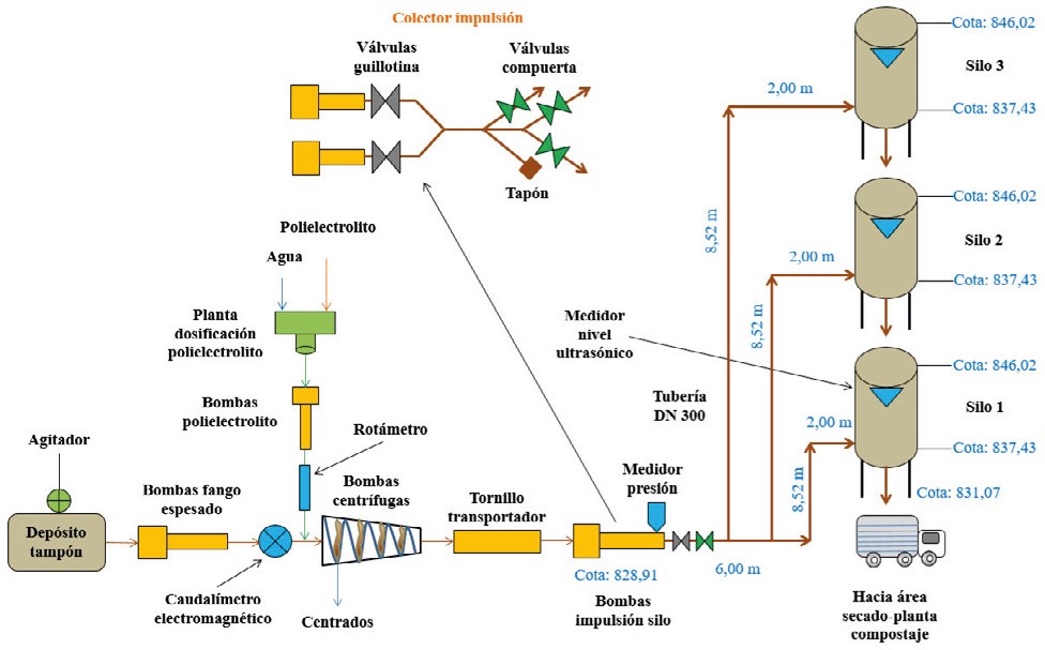
La figura 4 indica un esquema funcional del bombeo de fangos deshidratados al silo, que ha constituido el escenario de cálculo y donde se puede observar todo el equipamiento necesario para efectuar la deshidratación.
3.2 Equipamiento y datos de producción de fango
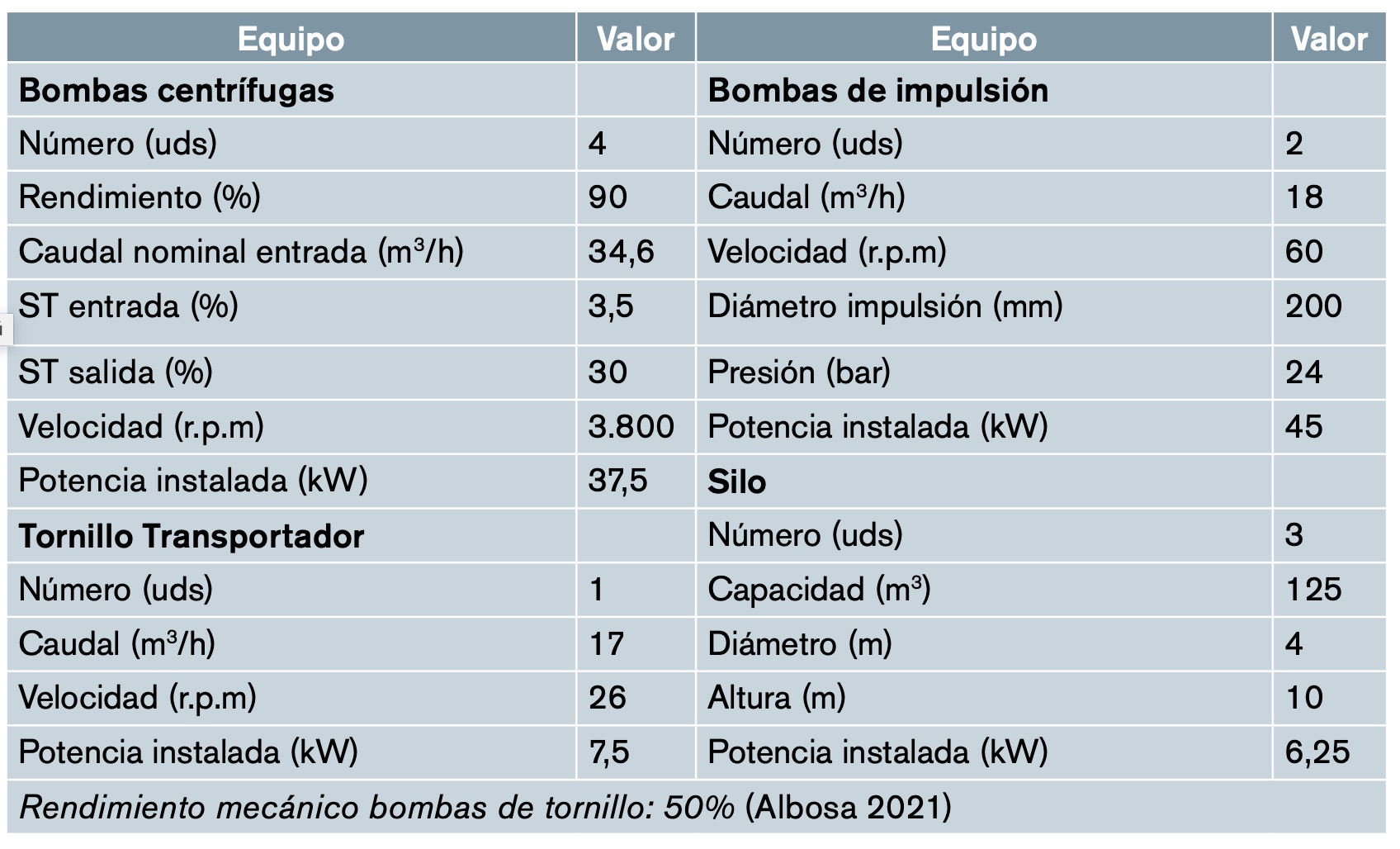
La tabla 1 indica las características principales del equipamiento necesario para efectuar la deshidratación.
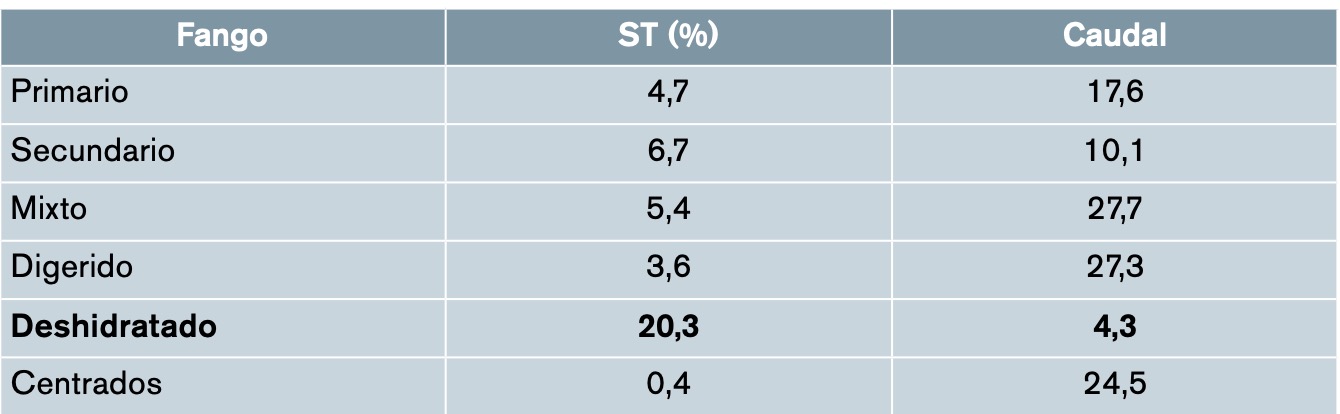
La tabla 2 muestra los valores medios de ST y caudal de los diferentes tipos de fangos producidos en la EDAR durante los años 2010-2016 (EDAR, 2022). Los datos del fango deshidratado constituyen el denominado punto de operación (PO), objeto de análisis.
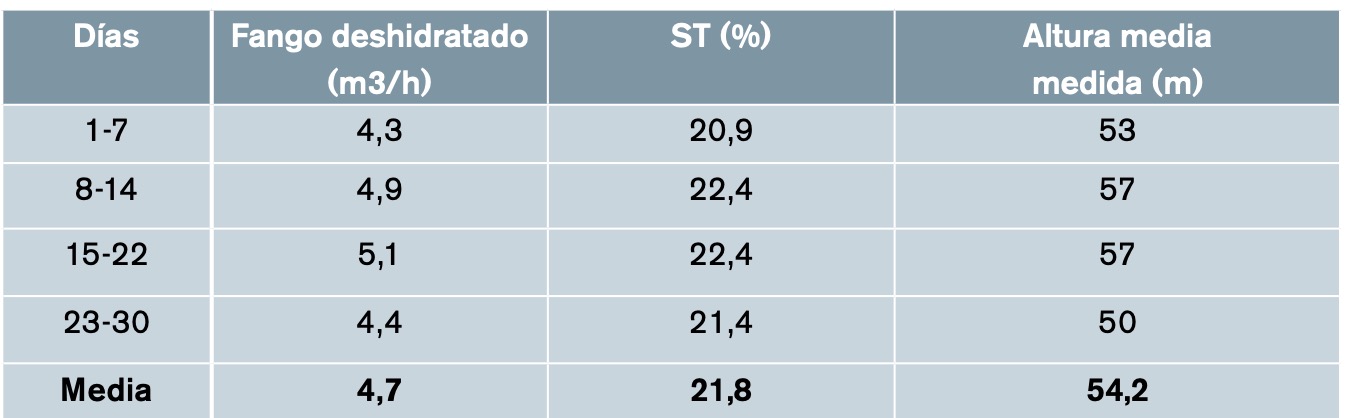
La tabla 3 presenta los datos de caudal de fango deshidratado, ST y altura media de impulsión tomada in situ en la EDAR durante el mes de marzo de 2016 agrupados en 4 semanas, con objeto de comparar, posteriormente, los resultados teóricos y experimentales.
Se han establecido 4 escenarios de análisis: el escenario 1 contempla la comparación entre los valores teóricos obtenidos y los experimentales de de la presión media de impulsión acontecidos durante el mes de marzo de 2016; el escenario 2 estudia la variación de una serie de parámetros con el valor ST en PO en función del caudal de fango deshidratado; el escenario 3 representa el análisis de sensibilidad de la impulsión variando el diámetro, ST y la longitud equivalente en función del caudal de fango deshidratado. Por último, el escenario 4 permite calcular el diámetro económico de la tubería de impulsión.
3.3. Ecuaciones necesarias
La ecuación (13) indica el cálculo de la altura total de impulsión (htotal, m).
La ecuación (14) permite obtener la pérdida de carga que experimenta un fluido al circular por una tubería según la ecuación de Darcy-Weisbach.
La ecuación (15) permite calcular la pérdida de carga directamente partiendo de las ecuaciones de Darcy-Weisbach, Poiseuille y número de Reynolds (Re, adimensional) considerando régimen laminar. La ecuación (16) indica el cálculo de la longitud equivalente de tubería (Leq) y la ecuación (17) el Re. Normalmente, al ser la velocidad máxima recomendable de circulación del fango deshidratado por las tuberías de impulsión de 0,06 m/s (Albosa, 2021), resulta Re < 2.300, lo que significa circulación en régimen laminar y se traduce en un valor para f establecido según la ecuación (18) de Poisseuille. La ecuación (19) indica la potencia teórica necesaria (P, kW) para bombear el fango deshidratado.
Donde hgeo es la altura geométrica (m); Δh, la pérdida de carga (m); Ltub la longitud de la tubería de impulsión (m); Lacc, la longitud equivalente de los accesorios (m); μ (η), la viscosidad dinámica (Pa.s) del fango; ρ, su densidad (kg/m3); Qfa, su caudal (m3/h); D, el diámetro de la tubería de impulsión (m); V, la velocidad (m/s); g, la aceleración de la gravedad (m/s2), y δb, el rendimiento mecánico de la bomba (%).
Para el cálculo de las pérdidas singulares se ha utilizado el método de la longitud equivalente aplicando los valores obtenidos del ábaco del Hydraulic Institute (Hydraulic Institute, 2022) en función del tipo de elemento singular considerado y de su diámetro.
3.4. Viscosidad dinámica
La tabla 4 indica los valores analíticos de la viscosidad absoluta del fango deshidratado en función de ST basados en datos suministrados por la empresa británica Mono, una de las líderes mundiales en la fabricación de bombas de cavidad progresiva y piezas afines (Albosa, 2021). En dichos datos, no se han tenido en cuenta la acción de factores como la temperatura, los sólidos volátiles, el pH, etc.
3.5. Diámetro económico
Se define la función coste anual de la impulsión de fango deshidratado C (€) mediante la ecuación (20) (Bernis, 2020), en la que C1 (€) es el coste correspondiente al consumo de energía eléctrica anual expresado en la ecuación (21) y C2 (€) es el coste anual de la inversión en tuberías, piezas especiales y válvulas indicado según la ecuación (22). Por otro lado, la ecuación (23) representa el valor del tipo de amortización de la inversión realizada (a, s.u.) (Bernis, 2020).
Donde, Nhoras es el número de horas anuales de funcionamiento de la impulsión (h), PEE es el precio unitario del suministro de energía eléctrica (€/kWh), Ptub, Pampl, Ptes, Pcodos, Pguill, Pcomp son los precios unitarios de las tuberías (€/ml), ampliaciones de diámetro, tes, codos, válvulas de guillotina y compuerta (€/ud), Nampl, Ntes, Ncodos, Nguill, Ncomp son el número de unidades de cada pieza especial (uds), r es el tipo de interés anual (s.u.) y t es el número de años de amortización (años).
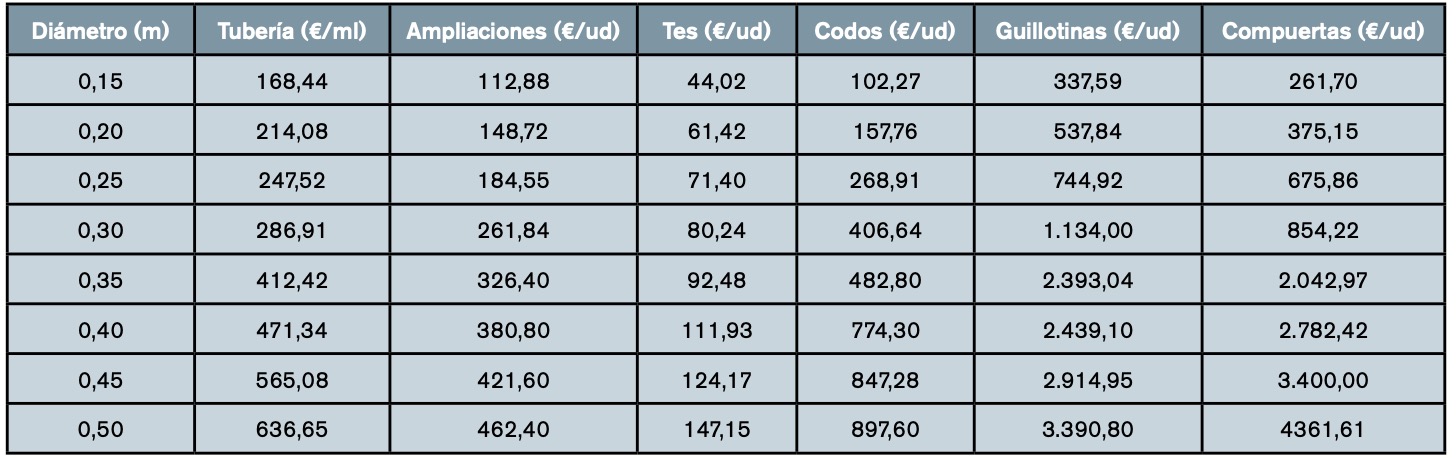
Se ha considerado que las bombas de fango deshidratado operan durante 8.760 h/año (50% bomba 1 y 50% bomba 2, caso real en la EDAR de Burgos), un precio de la energía eléctrica, solo término de energía, media de los 6 periodos P1-P6 tarifa ATR 6.2 (EDAR, 2022) de 0,1858 €/kWh (AEGE, 2022), un tipo de interés anual del 3% (Banco de España, 2017) y un periodo de amortización estimado de 25 años. La tabla 5 indica el valor del precio unita-rio de las tuberías, piezas especiales y válvulas en función del diámetro.
4. Resultados y discusión
4.1. Variación de ST del agua residual y fango
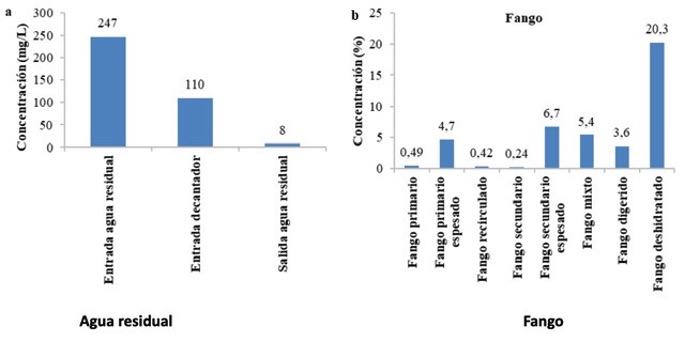
La figura 5a indica la variación de ST en las aguas residuales desde su entrada como agua bruta hasta su salida como depurada, mientras que la figura 5b presenta la variación del mismo parámetro para el fango (EDAR, 2022). La disminución de ST en el agua residual es del 96,8%, lo que da una idea de la efectividad del tratamiento realizado. El incremento de ST en el fango primario y secundario en los espesadores de gravedad y flotación es del 859% y del 2.691%, mientras que para el fango deshidratado es del 463,9%.
4.2. Viscosidad absoluta del fango en tubería y cavidad de la bomba
deshidratado.
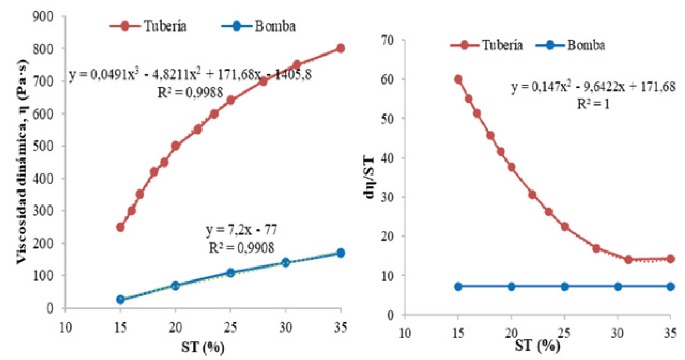
La figura 6a muestra la variación de la viscosidad del fango deshidratado en tubería y bomba en función de ST. La velocidad en la hidráulica de la bomba es mucho mayor que en la tubería. Por eso, su viscosidad es mucho menor, lo que, junto con el valor elevado del par de arranque, constituye un comportamiento típico del modelo de Herschel-Bulkley. Cuando ST es un 20%, la viscosidad en la bomba es 70 Pa·s y en la tubería 500 Pa·s, un valor el 614,3% superior. La viscosidad dentro de la bomba puede variar dentro de un estrecho margen de valores, 25-175 Pa·s, mientras que en la tubería varía entre 250 y 800 Pa·s. La figura 6b presenta los resultados de la curva d(η)/d(ST) en función de ST en tubería y bomba, donde se aprecia que el incremento relativo de la viscosidad en tubería es mucho más elevado para valores bajos que altos, puesto que la curva se va aplanando progresivamente a valores crecientes de ST, mientras que, en la bomba, este valor se mantiene constante.
4.3. Pérdida de carga y energía
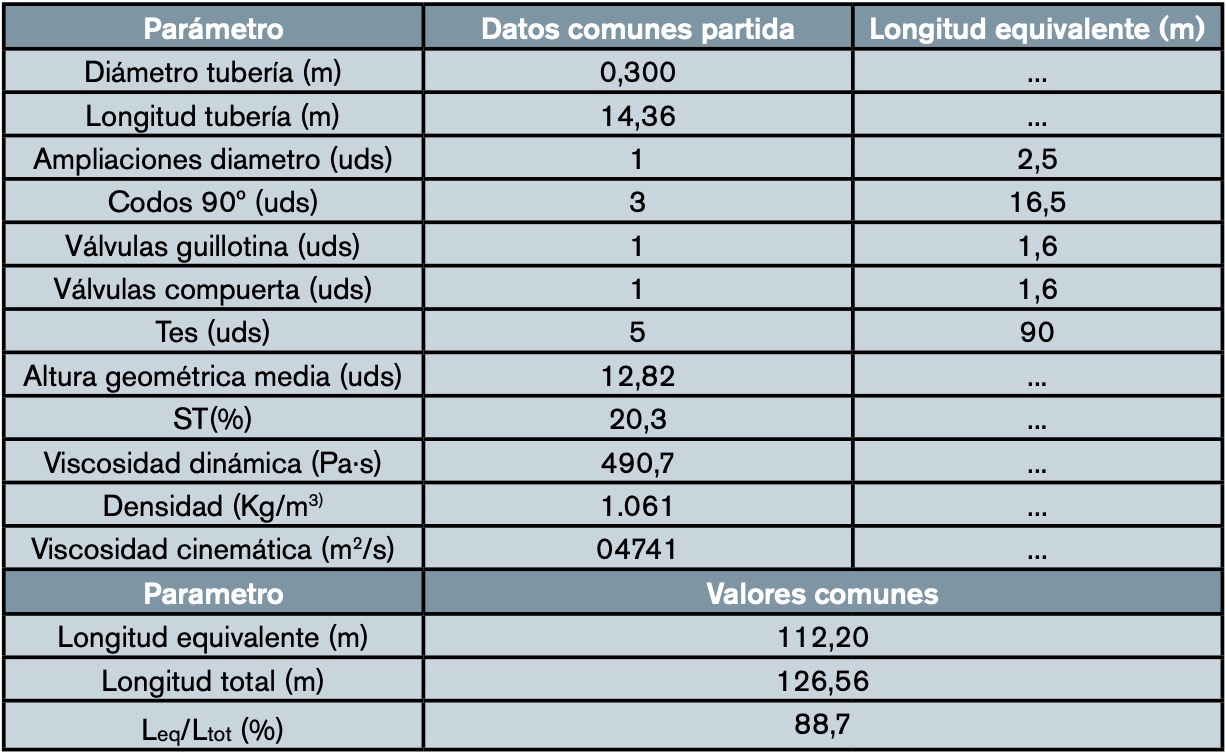
La tabla 6 indica los datos comunes de partida y los valores obtenidos para el cálculo de los escenarios 1, 2, 3 y 4. La viscosidad cinemática del fango para ST del 20,3% es 0,4741 m2/s, mientras que la del agua a 20 ºC es de 1,008·10-6m2/s, o sea 470.337 veces más elevada, lo que da una idea de las enormes fuerzas de cizalla existentes en las paredes de las tuberías que se oponen al movimiento del fluido. El colector de salida, con todas las piezas especiales y válvulas, origina una elevada pérdida de carga del orden del 71,1% del total. A continuación, en orden de magnitud, se encuentran los 3 codos de radio largo de 90 grados, que originan unas pérdidas de carga del 13%. La longitud equivalente del circuito supone el 88,7% del total, lo que indica la gran importancia que tiene la correcta predisposición de los elementos singulares para reducir la pérdida de carga.
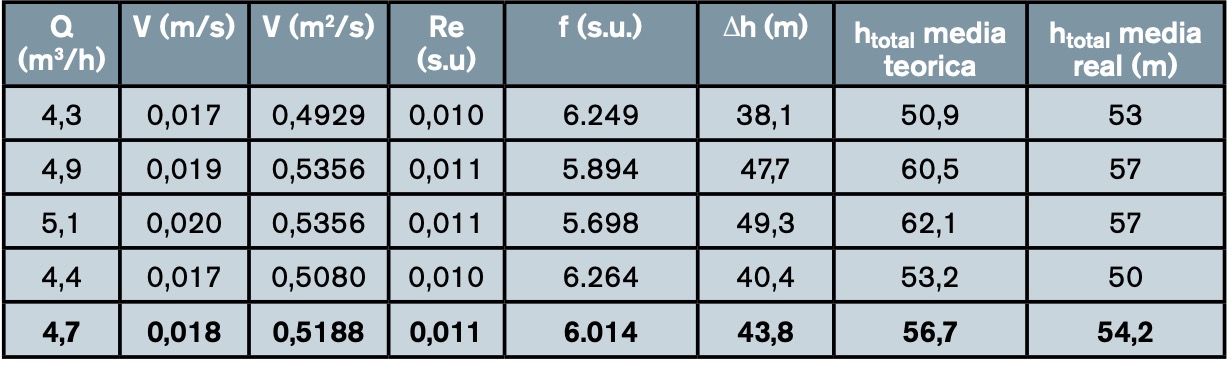
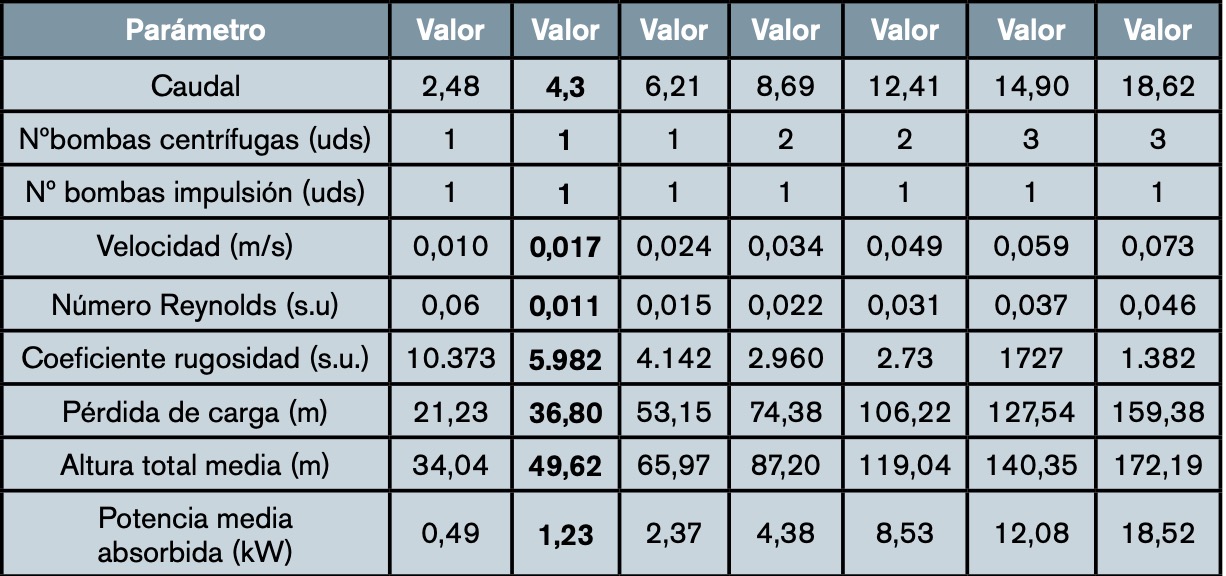
La tabla 7 muestra los resultados obtenidos de forma teórica y experimental de la altura de impulsión acontecidos La tabla 8 representa los resultados teóricos obtenidos de pérdida de carga y energía en la impulsión del escenario 2 para el caso ST 20,3% en función del caudal de fango deshidratado. Los resultados obtenidos en el PO de la planta han sido señalados en negrita.
Cuando operan 3 bombas centrífugas a caudal nominal impulsando por una sola tubería, la velocidad es de 0,073 m/s, el 21,7% superior a la máxima recomendada de 0,06 m/s. La velocidad en PO es 0,017 m/s < 0,06 m/s, el 71,7%. Sin embargo, al estar las tuberías dispuestas en paralelo, el máximo caudal que puede circular por cada una de ellas es 5,5 m3/h, que es la capacidad nominal de cada bomba centrífuga, aunque se ha analizado el caso de fluir todo el caudal por una sola tubería.
Resultan unos valores de Re muy bajos, del orden de 0,011, muy distantes del valor de 2.300 que marca la separación entre flujo laminar y turbulento. Esto indica una muy clara circulación en régimen laminar. El valor de f es 5.982, muy elevado en comparación con los obtenidos normalmente para el caso del agua de 0,010-0,020. El valor de f es tanto más grande cuanto más pequeño sea el caudal, pues f es inversamente proporcional al valor del Re, que sigue la tendencia contraria. Por otro lado, f disminuye proporcionalmente al aumentar el caudal; sin embargo, la pérdida de carga aumenta en función de su cuadrado, por lo que esta variable en su conjunto aumenta.
4.4. Estudio de sensibilidad
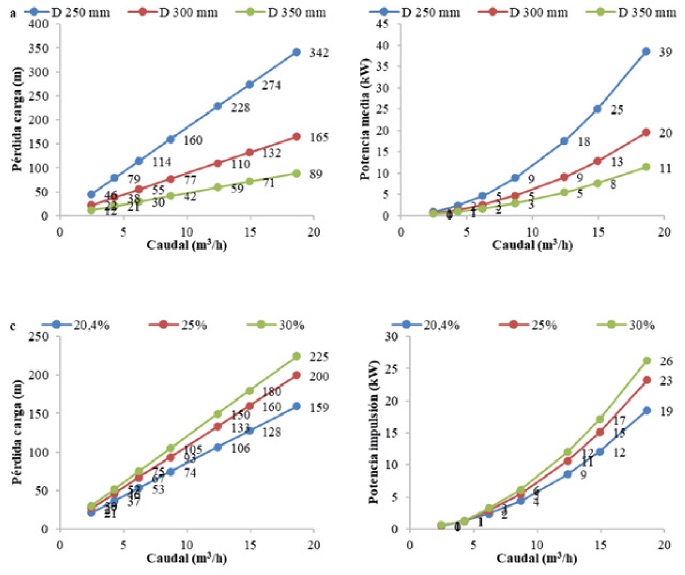
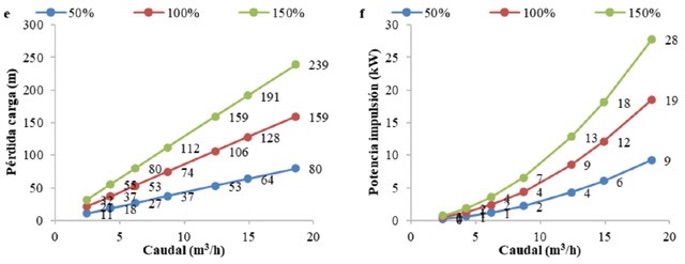
La figura 7 representa los resultados del escenario 3. Las figuras 7a y 7b visualizan la variación de la pérdida de carga y la potencia media consumida en función del caudal de fango deshidratado variando el diámetro. La figura 7c y 7d indica lo mismo, variando ST. Finalmente, la figura 7e y 7f, ídem modificando la longitud equivalente.
En todos los casos se puede observar la variación lineal de la pérdida de carga con el caudal. Sin embargo, la potencia absorbida varía de forma cuadrática, pues depende de Qfa2. La altura máxima total de bombeo para caudal máximo y ST 30% (ST máximo de las bombas centrífugas) alcanza el valor de 225 m en PO, valor que identifica plenamente la instalación de esta bomba de 24 bares de presión. Destaca la reducción en la pérdida de carga al modificar el diámetro, por ejemplo, de 300-350 mm (incremento D =16,7%), pues disminuye el 46,1% y la potencia absorbida, el 45%. Por otro lado, se observa el gran incremento en la pérdida de carga cuando se disminuye el diámetro a 250 mm, aumentando el 107,3% y la potencia el 95%. Se observa que cuanto mayor es ST, menor es el incremento relativo en la pérdida de carga, pues sigue la curva η= f(ST). El incremento o disminución de la longitud equivalente influye de forma directamente proporcional en la pérdida de carga con iguales incrementos.
4.5. Diámetro económico
diámetro.
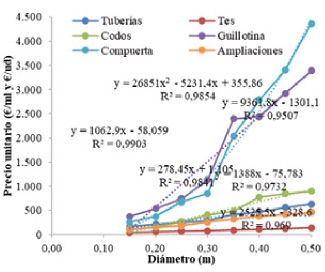
La figura 8 representa las líneas de tendencia y coeficientes de correlación R2 del precio unitario de las tuberías, piezas especiales y válvulas en función del diámetro de la tubería. Se observa el comportamiento lineal de cinco de los seis precios unitarios representadosen función de D, y solo resulta el precio de las válvulas de compuerta con una variación de tipo cuadrática. Para calcular el diámetro económico de la impulsión, se deriva la función C con respecto a D e iguala a cero, o sea:
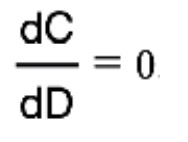Posteriormente, se sustituye D en la segunda derivada:
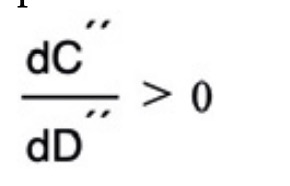Y si el resultado obtenido es mayor que cero, entonces D hará que el valor de la función C sea mínimo, y se denomina diámetro económico Decon (m) de la impulsión.
La ecuación (24) indica el valor de C en función del diámetro de la tubería D.
Derivando nuevamente la ecuación (25) con respecto a D se obtiene la ecuación (26).
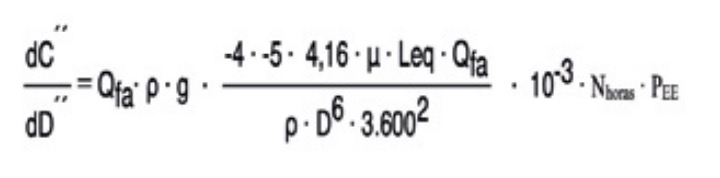Sustituyendo el D calculado según la ecuación (25) en la ecuación (26), se puede observar que:
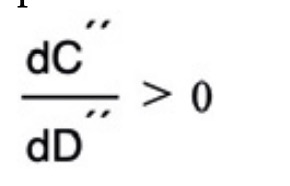luego indica que Decon es un valor que hace mínima la función C, coste de la impulsión.
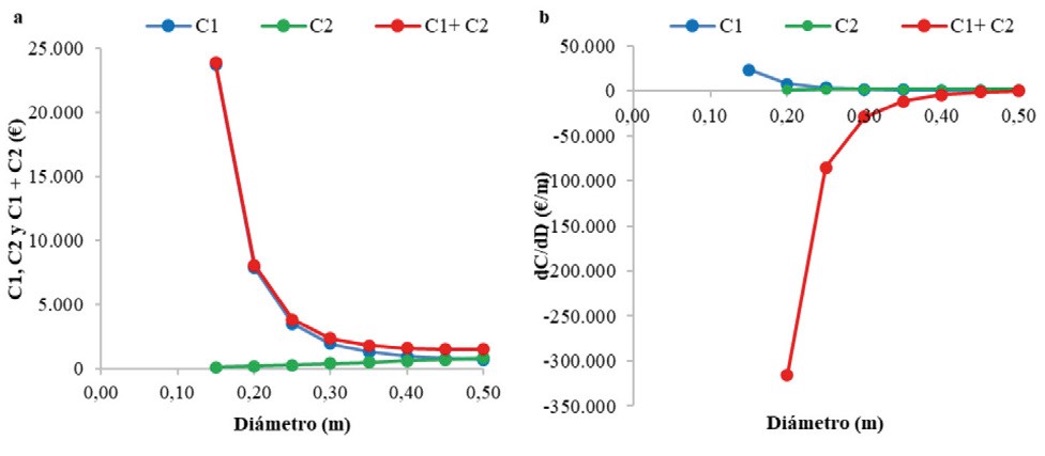
La figura 9a representa las tres funciones de coste anteriores, C1, C2 y C = C1 + C 1 y la figura 9b su derivada con respecto a D, ambas en función de D, con los valores del PO.
Se observa en la figura 9a la variación prácticamente lineal creciente del coste de la inversión en tuberías, piezas especiales y válvulas, en contraste con el carácter potencial decreciente de la función coste de la energía eléctrica. El valor del diámetro económico que ha hecho mínimo el coste anual de la impulsión operando durante un periodo de 25 años ha resultado ser Decon=0,450 m. La figura 9b indica claramente que cuando D tiende a ∞, dC1/dD ≈ 0 y d[C1 + C2]/dD ≈ dC2/dD
La tabla 9 muestra cómo varía Decon en función del incremento de 10 variables presentes en las ecuaciones (21) y (22). De las variables incrementadas, el Decon aumenta con seis de ellas, disminuye en tres y no le afecta en una.
5. Conclusiones
La gran diferencia entre los valores de la viscosidad dinámica en tubería y bomba demuestran fielmente el carácter no newtoniano del fango deshidratado. Su tendencia a la disminución no lineal al incrementarse la velocidad de deformación junto con la necesidad de un elevado par de arranque en la bomba para vencer la tensión umbral, ndican claramente que este fluido sigue el modelo de Herschel-Bulkley. La pérdidade carga es directamente proporcional al valor del caudal, viscosidad y longitud equivalente, e inversamente proporcional al diámetro elevado a la cuarta potencia mientras la pérdida de energía es directamente proporcional al cuadrado del caudal de fango deshidratado a igualdad de los demás parámetros. Las tes, codos y demás piezas especiales son los principales responsables de las pérdidas de carga en la impulsión, alcanzando hasta el 90% del total. Se puede afirmar que tanto la elección de las piezas especiales como el diámetro de la tubería son los factores más importantes a tener en cuenta en el diseño de una impulsión de fango deshidratado. El cálculo del diámetro económico depende de un total de 10 variables independientes, que deben ser elegidas convenientemente. El valor del precio actual de la electricidad distorsiona el valor del diámetro económico hacia valores más altos que cuando su precio era inferior.
Agradecimientos
Desearía dar las gracias a D. Pablo Piedras Romero, director de la empresa Alternativas de Bombeo S.A. y a D. Arsenio Costilla Rodríguez, jefe de planta de la EDAR de Logroño (anteriormente de Burgos), por la inestimable ayuda recibida a la hora de conseguir los datos necesarios para poder elaborar este artículo.
Referencias
AEGE (2022). Barómetro energético en España. https://www.aege.es/barometro-energetico-espana/, acceso septiembre 2022.
Albosa (2021). Análisis del transporte de fango deshidratado. Cortesía de Albosa.
Almesa (2022). Tuberías de acero inoxidable. www.almesa.com, acceso agosto 2022.
Banco de España (2017). Tabla de tipos de interés. http://www.bde.es/clientebanca/es/areas/Tipos_de_Interes / Tipos_de_interes/Otros_tipos_de_i/ otros-tipos/Tabla _ tipos_de_interes_ legal.html, acceso agosto 2022.
Bergadá-Grañó J. (2012). Mecánica de fluidos. Breve introducción teórica con problemas resueltos. https://www.researchgate.net/profile/JBergada/publication/262698142, acceso agosto 2022.
Bernis F (2020). Diseño económico de tuberías. Diámetro óptimo en impulsiones. https://www2.uned.es/ca-tortosa/ Biblioteca_Digital/Biblio/JM_Franquet/Disen_economico.pdf, acceso agosto 2022.Betancourt-Grajales R (2022). Fenómenos de transferencia. Transferencia molecular de calor masa y cantidad de movimiento. https://pdfcoffee.com, acceso agosto 2022.
EDAR (2022). Estación depuradora de aguas residuales de Burgos.
Gardea-Villegas H (2008). Dos propuestas para el proyecto del bombeo de fluidos no newtonianos. Caso de los fangos residuales de plantas de tratamiento de aguas negras. Ingeniería, investigación y tecnología IX, 2, 87-97. https://www. redalyc.org/pdf/404/40490201.pdf.
Haldenwang R, Sutherland APN, Fester VG, Holm R and Chhabra RP (2012). Sludge pipe flow pressure drop prediction using composite power-law friction factor–Reynolds number correlations based on different non-Newtonian Reynolds numbers. ISSN 0378-4738 (Print) = Water SA Vol. 38 No. 4 July 2012. http://dx.doi.org/10.4314/wsa. v38i4.17. Hong E, Yeneneh AM, Sen TK, Ang HM, Kayaalp A (2017). The relationship between physico-chemical and rheological characteristics of digested sludge, biosolid, centrate and the effects on dewatering performance (A case study). Journal of Water Process Engineering, 19, 193-204. https:// espace.curtin.edu.au/bitstream/ handle.
Hydraulic Institute (2022). The Global Authority on Pumps and Pumping Systems. https://www.pumps.org, acceso agosto 2022.
Hydraulic Institute (2022). The Global Authority on Pumps and Pumping Systems. https://www.pumps.org, acceso agosto 2022.
Levenspiel (2022). Capítulo 5. Fluidos no newtonianos. http://sgpwe.izt. uam.mx/files/users/uami/hja/file/ Mec_Fluid_ CBS/Fluidos_No _Newtonianos_Levenspiel. pdf, acceso agosto 2022.
Martín I, Salcedo R, Font R (2011). Mecánica de fluidos. Tema1. Flujo interno de fluidos incompresibles y compresibles. https://rua.ua.es/dspace/ bitstream, acceso agosto 2022.
Navarro S, Almera J, Botero F, Vargas P (2007). Unidad 1, Fenómenos de transporte. Hidrostática. https:// marcanord.files.wordpress. com/2012/11/unidad, acceso agosto 2022.
Panchi Guanoluisa AN (2013). Determinación de parámetros reológicos en bebidas de frutas con diferentes concentraciones de sólidos solubles mediante el uso del equipo universal TA–XT2I. https://repositorio.uta.edu.ec/bitstream, acceso agosto 2022.
Seyssiecq I, Ferrasse JH, Roche N (2003). State-of-the-art: rheological characterisation of wastewater treatment sludge. Biochemical Engineering Journal 16 (2003) 41–56. Doi: 10.1016/S1369- 703X(03)00021-4.
Talis Belgicast (2022). www.belgicast.eu, acceso agosto 2022.
