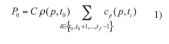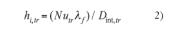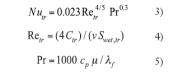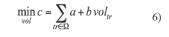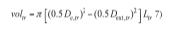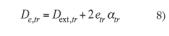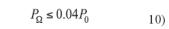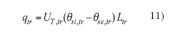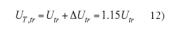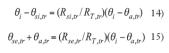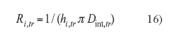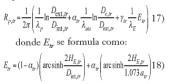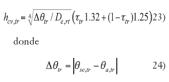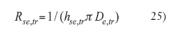Modelo matemático de optimización para aislamiento térmico conforme a la norma EN ISO 12241:2008
RESUMEN
El presente artículo muestra el modelo matemático de optimización del aislamiento en instalaciones térmicas basado en la norma EN ISO 12241:2008, utilizada como procedimiento alternativo en la Instrucción Técnica 1.2.4.2.1.3. del R.D. 1027/2007, de 20 de julio, por el que se aprueba el Reglamento de Instalaciones Térmicas en Edificios.
Recibido: 7 de agosto de 2011
Aceptado: 13 de abril de 2012
Palabras clave
Código Técnico de la Edificación, aislamientos, conductividad, agua caliente sanitaria, modelos matemáticos
ABSTRACT
This paper presents the mathematical optimization model of thermal isolation facilities based on EN ISO 12241:2008, used by the alternative procedure in Technical Instruction 1.2.4.2.1.3. the R.D. 1027/2007 of 20 July, which approves the Regulation of Thermal Installations.
Received: August 7, 2011
Accepted: April 13, 2012
Keywords
Technical Building Code, insulation, conductivity, domestic hot water, mathematical model
Los modelos matemáticos ayudan a describir, explicar y predecir parte de la realidad en que residen los problemas y son una técnica vital en el mundo de la ingeniería. Con la ayuda de modelos y herramientas computacionales adecuados se puede encontrar en un tiempo razonable la solución óptima a un problema.
El valor económico de las instalaciones adquiere gran relevancia en cualquier obra, máxime en periodos de crisis. Por otro lado, el cumplimiento legislativo aplicable nos aporta restricciones mínimas y procedimientos de cálculo. La unión de estos dos aspectos comporta no pocas discusiones entre el proceso de reingeniería y selección de los departamentos técnico y de compras de las constructoras (que buscan un precio de cierre siempre inferior) y las empresas instaladoras (que evitan instalar equipos o materiales no obligatorios). Ello unido a la fuerte competitividad hace que los márgenes de beneficios sean mínimos y tocar cualquier punto dentro de una instalación sea vital de cara al éxito.
En las instalaciones de agua caliente sanitaria (ACS), la necesidad de aislar las tuberías para evitar fugas térmicas supone el aumento de precio de la instalación.
El valor del aislamiento puede llegar a ser entre 2 y 4 veces el precio de la tubería que transporta el fluido.
Por ello, se necesita un modelo matemático que ayude a encontrar la solución óptima de aislamiento, sin consumir recursos de tiempo, personal y trabajo (innecesarios en muchos casos) para la mejora de la competitividad y el aumento del beneficio social.
Estudio previo
Las tuberías de una instalación se disponen según las características de uso y funcionalidad que deban seguir (Soriano Rull, 2008). Tendremos tuberías enterradas de aplicación para acometidas y, esporádicamente, instalaciones generales; vistas, no frecuentes en el ámbito doméstico aunque sí en entornos donde predominen criterios de funcionalidad y accesibilidad sobre la estética (industrias, comercios, hospitales, etcétera), y ocultas o empotradas sobre falso techo, en el interior de canales o bandejas aptas para tal fin, como se muestra en la figura 1.
En las instalaciones empotradas directamente en las paredes y tabiques de obra, se cuida el contacto directo de las tuberías con los elementos de cobertura. Para evitar corrosiones de la tubería por reacción química con los materiales de construcción se utilizan envolventes que puedan realizar funciones complementarias como: térmicas, acústicas o de señalización. La figura 2 muestra un ejemplo de ello.
Los materiales de los tubos aptos en las instalaciones de agua potable según el apartado 6.2. del DB HS 4 Suministro de Agua (CTE, 2009), corresponden a:
– Acero galvanizado
– Cobre
– Acero inoxidable
– Fundición dúctil
– Policloruro de vinilo no plastificado (PVC)
– Policloruro de vinilo clorado (PVC-C)
– Polietileno (PE)
– Polietileno reticulado (PE-X)
– Polibutileno (PB)
– Polipropileno (PP)
– Multicapa de polímero / aluminio / polietileno resistente a temperatura (PE-RT)
– Multicapa de polímero / aluminio / polietileno reticulado (PE-X)
La selección de un plástico específico requiere especial atención. Hay que remitirse a los gráficos proporcionados por los fabricantes o distribuidores para verificar los rangos de funcionamiento de temperatura y de presión.
La relación de diámetros en la distribución interior de una vivienda suele oscilar entre 12-25 mm (para tuberías de cobre). Las velocidades de cálculo están comprendidas entre 0,50 m/s y 2,00 m/s (para tuberías metálicas) o 3,50 m/s (para tuberías termoplásticas o multicapas). Las presiones mínimas deben ser de 0,10 MPa en grifos comunes y 0,15 MPa para fluxores y calentadores, sin sobrepasar los 0,50 MPa la presión en cualquier punto de consumo (CTE, 2009).
La conductividad térmica de los materiales utilizados debe incrementarse por factores que tengan en cuenta las influencias de la diferencia de temperatura real del material instalado, la puesta en obra, las variaciones en densidad o las modificaciones estructurales.
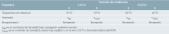
La conductividad térmica de laboratorio utiliza valores medidos de acuerdo con métodos internacionales o nacionales equivalentes, tales como: caja caliente guardada según la norma ISO 8302, método del flujo de calor según la norma ISO 8301 o caja caliente según la norma ISO 8990. Para evitar conversiones hacia valores declarados se recomienda que las medidas se lleven a cabo bajo los con-juntos de condiciones a o b con temperatura de referencia 10 ºC o 23 ºC, respectivamente, mostrados en la tabla 1 (ISO, 1999).
La norma ISO 13787 proporciona un método que permite determinar la conductividad térmica declarada a partir de la conductividad térmica de laboratorio. Otra aproximación que permite determinar los valores declarados viene dada por la ASTM C680-89.
La conductividad térmica declarada dada por el fabricante debe considerar las fluctuaciones ligadas a los procesos de fabricación. Si la conductividad térmica declarada se toma como base en el caso del aislamiento de tuberías, es posible que este valor incluya estos parámetros. Sin embargo, es responsabilidad del instalador asegurarse de que estos facto-res tienen un orden de tamaño significativo (Massó Moreu, 2008).
El material de las coquillas utilizadas en el aislamiento de tuberías destinadas para el ACS suele ser: de espuma elastomérica flexible o de espumas de célula cerrada fabricada a base de caucho natural o sintético con otros polímeros (IDAE, 2008).
Descripción del problema y análisis de datos iniciales
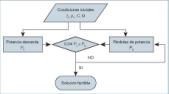
Conocidos los elementos que intervienen en el problema, principales características y los criterios de instalación, a continuación, se describen las características del modelo siguiendo el esquema de la figura 3.
Se parte de las condiciones iniciales: de temperatura, de presión y de caudal de agua a la entrada de la caldera o cualquier otro dispositivo de similar función, del esquema del sistema hidráulico y de las temperaturas en los recintos por los que discurre la instalación.
Para la temperatura a la entrada de la caldera se asume un valor igual a la temperatura media del agua de red. La presión es la calculada en el punto de entrada a la caldera tras el dimensionado hidráulico, así como el caudal en cada tramo previsto por el proyectista.
No hay que olvidar que todas las tuberías y accesorios de las instalaciones térmicas dispondrán de aislamiento térmico cuando contengan fluidos con temperatura mayor de 40 ºC instalados en locales no calefactados, entre los que se deben considerar: pasillos, galerías, falsos techos y suelos técnicos, entre otros (BOE, 2007).
En toda instalación térmica por la que circulen fluidos no sujetos a cambio de estado, en general las que el fluido caloportador es agua, las pérdidas térmicas globales por el conjunto de conducciones no superarán el 4% de la potencia máxima que transporta (BOE, 2007).
El trazado de la instalación se configura por tramos que podrán ser: verticales u horizontales; aislados o desnudos, y empotrados en el interior de rozas o libres en los falsos techos, suelos técnicos o patinillos.
La potencia que requiere el fluido (agua) depende del caudal demandado y de las condiciones iniciales del fluido. El calor específico es función de la temperatura y de la presión (IAPWS, 2007) y se define como la cantidad de energía a suministrar por unidad de masa para elevar su temperatura un grado. Por tanto, la potencia para abastecer la demanda será el caudal a la entrada del sistema por la densidad del fluido en las condiciones iniciales de temperatura y presión, por la sumatoria del calor específico desde la temperatura inicial hasta la temperatura final menos un grado, en pasos de 1 ºC.
Para el cálculo de las pérdidas energéticas en cada tramo, se sigue el esquema de la figura 4, que muestra el esquema térmico y su equivalente eléctrico.
La resistencia de convección interna Ri,tr es constante dado que depende sólo de las condiciones del fluido. El resto de resistencias dependen del espesor del aislamiento, conductividad de los materiales de la tubería y del aislante. También, de la temperatura ambiente que rondará los 23-25 ºC en verano y los 2123 ºC en invierno o cualquier otra temperatura conforme la UNE-EN ISO 7730 dentro de los recintos calefactados.
El coeficiente de convección interior en una tubería se define como:
A su vez, el número de Nusselt cuando los fluidos se enfrían depende del número de Reynolds y el número de Prandtl,
Los parámetros de viscosidad cinemática, viscosidad dinámica, conductividad térmica y calor específico pueden ser calculados a través de las fórmulas propuestas en Sengers y Kamgar-Parsi (1984), IAPWS (2003), IAPWS (2007) y IAPWS (2008).
La expresión (3) es válida siempre y cuando 0,7 < Pr <160, Retr ≥ 10000 y la relación Ltr / Dint, tr >10. Los límites de validez tanto para el número de Prandtl como para el de Reynolds se cumplen de forma general por las instalaciones convencionales. Tan sólo puede no satisfacerse la relación Ltr / Dint, >10 en algunos tramos pequeños, como aquellos en los que van instalados las válvulas de corte de los cuartos húmedos.
Tras analizar los costes de material tomando como referencia PVP de catálogos de dos fabricantes para un mismo tipo de material, evaluados dentro del rango de diámetros usuales utilizados en la distribución interior de viviendas, se pueden aproximar a curvas de coste line-ales, tal como muestra la figura 5. Las rectas de coste están acotadas por el espesor mínimo que el fabricante posea dentro de su gama.
El modelado lineal del coste del aislamiento simplifica el problema de programación matemática al convertirse en un problema continuo y no discreto (como sucede en la realidad).
Modelo matemático
La formulación (1)-(5) nos ha servido para calcular los parámetros iniciales de la instalación necesarios en el problema de
optimización. Por tanto, ya se está en condiciones para desarrollar, formular y comprender el modelo matemático que nos ayudará a encontrar la solución óptima.
El problema de optimización se basa en la minimización del espesor del aislamiento (6), sujeto al conjunto de restricciones (7)-(25) físicas (ISO, 2008) y legales (BOE, 2007).
Finalmente, se recordarán y analizarán otros conceptos de ingeniería térmica definidos en la expresión (26).
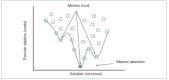
El problema de optimización es de naturaleza no lineal. Por eso, debemos usar paquetes de software capaces de resolver problemas de programación matemática no lineales. Cualquier paquete de software del tipo NLP (nonlinear programming), nos proporciona una solución localmente óptima que no tiene por qué coincidir con el óptimo absoluto, aunque sí puede aproximarse bastante, como representamos en la figura 6.
Dado que tratamos el problema de forma continua, al pasar los resultados óptimos obtenidos a valores de espesor comerciales (que serán los inmediatamente superiores o iguales a los óptimos por tramo encontrados) la solución óptima local es un buen resultado de cara a la reducción de costes de aislamiento.
Nuestra función objetivo consiste en minimizar el coste total del aislamiento en la instalación, que corresponde a la sumatoria del coste de aislamiento en el con-junto de tramos de la instalación.
No se suele mezclar marcas de aislamiento; por tanto, los parámetros a y b que definen la recta de coste son únicos para todo el problema.
Se podría plantear con qué fabricante se obtiene un mayor beneficio para el aislamiento óptimo, pero ese análisis queda fuera de los objetivos del presente artículo. También se pueden complementar los datos de entrada con la norma UNE 92301, que nos indica los criterios de medición para trabajos de aislamiento térmico (AENOR, 2002), ya que el material que se compra no es aprovechado al 100% en la instalación, repercutiendo costes adicionales.
El volumen de aislamiento por tramo queda definido por la ecuación:
El espesor del aislamiento condiciona el diámetro exterior del conjunto tubería-coquilla afectando a los parámetros de resistencia de convección exterior y resistencia del conjunto, tal que:
Las pérdidas globales de la instalación se calculan como la suma de pérdidas unitarias en el conjunto de tramos de la instalación.
Las pérdidas térmicas globales no deberán superar el 4% de la potencia máxima que transporta.
Las pérdidas en cada tramo quedan definidas como:
La transmitancia térmica del tramo incluye un factor correctivo debido a los puntos singulares (anclajes, conexiones entre tuberías, válvulas, etcétera) que desprecia la existencia de los puentes térmicos. La norma EN ISO 12241:2008 establece un factor de 0,15 debido a los puntos singulares.
La transmitancia del tramo corresponde a la inversa de la resistencia equivalente total del esquema equivalente eléctrico mostrado en la figura 4.
Las temperaturas superficiales en el conjunto tubería-coquilla se estiman gracias a la dualidad que existe entre la ingeniería eléctrica y la térmica, aplicando un divisor de tensión en el que la temperatura es el dual de la tensión.
La resistencia térmica del interior de la tubería sólo depende de las condiciones del fluido, calculándose como:
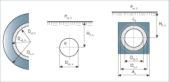
La resistencia del conjunto tuberíacoquilla depende, además de las características de los materiales de la tubería y del aislamiento, de factores de instalación (aislado o no aislado, empotrado o no empotrado) y del espesor del aislante. El valor del parámetro a es 1 si está aislado y 0 si no lo está. El parámetro g indica si el tramo está empotrado en cuyo caso toma un valor 1 o 0 si no está empotrado. La figura 7 muestra algunos de los parámetros más importantes a la hora de desarrollar las expresiones (17)-(20).
Suponiendo una distancia mínima de 10 mm desde la superficie de la pared hasta la cara externa del conjunto tubería-coquilla, la profundidad del empotramiento queda como:
La emisividad ε para superficies no metálicas es de 0,94 y la constante de Stefan-Boltzmann σ es de 5.67E-8 W m-2 K-4.
La parte convectiva del coeficiente superficial de transmisión de calor depende de factores como el movimiento del aire, temperatura, orientación relativa y material.
El régimen laminar o turbulento se define según la EN ISO 12241 como De3 Δθ siendo turbulento cuando D3 Δθ > e 10 m3 K y laminar De3 Δθ ≤ 10 m3 K. Si despejamos el diámetro exterior para un Δθ = 60 K se obtiene un diámetro de 55 cm. Este valor supera el espesor de los tabiques y, por tanto, se deshecha la condición de régimen turbulento por estar fuera de las condiciones reales de instalación.
Dentro del régimen laminar se distingue entre la orientación vertical y horizontal, de manera que el coeficiente de convección laminar para tuberías es de:
El parámetro τ nos indica la orientación vertical (τ = 1) u horizontal (τ = 0) de la tubería.
Si se observa la ecuación del coeficiente superficial externo de transmisión de calor (21), es función de si misma a través de la temperatura superficial externa (15) que se formula como:
Es necesario realizar una serie de iteraciones para encontrar el valor exacto de hse,tr.
Otro concepto que recordamos en este artículo es el radio crítico. El aumento del aislamiento conlleva elevar la resistencia térmica, pero también el área de transmisión de calor (Incoprera, 1999). Existe un determinado valor a partir del cual el flujo de calor decrece, y es formulado como sigue:
Este fenómeno es aplicable en tuberías o conductos delgados como los que se están trabajando en los sistemas hidráulicos de ACS. convencionales. Si el radio exterior del conjunto tuberíacoquilla es inferior al radio crítico, la adición de aislamiento provoca el aumento de las pérdidas energéticas y si el radio exterior del conjunto es superior al radio crítico, cualquier adición de aislamiento reduce las pérdidas.
Este concepto nos ayudará a saber hacia dónde tiende el valor óptimo de espesor.
Ejemplo de estudio y aplicación del modelo
El siguiente ejemplo de estudio presenta la distribución de ACS. de una vivienda unifamiliar cuyos datos del cálculo hidráulico y trazado de la instalación se exponen a continuación.
La temperatura del agua a la entrada de la caldera es de 10 ºC, se quiere elevar dicha temperatura hasta los 50 ºC. El caudal máximo instantáneo es de 0,49 dm3 s-1. La presión de entrada a la caldera es de 20,64 m.c.a. (0,202404 MPa).
La instalación se realiza con tubería multicapa polímero/aluminio/PE-RT, cuya conductividad es de 0,40 W m-1 K-1.
El material de las coquillas es de espuma elastomérica basada en caucho sintético con una conductividad térmica declarada a 10 ºC de 0,04 W m-1 K-1.
Las rozas van a ser selladas con un mortero blanco para enfoscar con una conductividad térmica de 0,78 W m-1 K-1.
Se escoge un fabricante cuya recta de coste es de a = -0,3254 € y b = 1,6588 € dm-3.
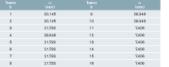
El trazado de la instalación se describe en la tabla 4.
Para los diámetros de los tramos anteriores les corresponden un espesor de 25 mm de aislante de conductividad 0,04 W m-1 K-1, aplicables a los tramos que discurren por los falsos techos (tramos 1-10). Los tramos empotrados (del 11 al 16) corresponden a las velas y no será necesario su aislamiento por encontrarse empotrados dentro de locales calefactados.
A partir de estos datos la potencia térmica que transporta el fluido es de 81953 W.
Las resistencias de convección internas por tramos se reflejan en la tabla 5.
Para la resolución del problema se utiliza un PC con procesador AMD Athlon(m) 1,25 GHz, 512 Mb de RAM, aplicando el paquete de optimización CONOPT 3. Para buscar el valor de hse,tr se itera 10 veces utilizando como valor inicial de 10 W m-2 K-1 en todos los tramos.
Si se fuerza el modelo con los espesores indicados en la tabla 1.2.4.2.1. del RITE, se obtiene unas pérdidas globales de 193,793 W. El coste del material aislante es de 79,888 €. La resolución se obtiene en 6,938 segundos. La tabla 6 muestra los resultados de coeficiente h
se,tr y de las pérdidas por tramo.
Si se aíslan las velas con el espesor correspondiente al RITE, se obtiene unas pérdidas de 137,559 W. El coste del material aislante es de 126,139 €. La resolución se obtiene en 8,859 segundos. La tabla 7 muestra los resultados de coeficiente hse,tr y de las pérdidas por tramo.
Si no se aísla ninguna tubería, las pérdidas serían de 243,943W. El coste de material aislante es de 0 €. La resolución se obtiene en 5,797 segundos. La tabla 8 muestra los resultados de coeficiente hse,tr y de las pérdidas por tramo.
El radio crítico para este último caso corresponde a los valores de la tabla 9.
Conclusiones
Las consecuencias que tiene el aislar las velas en la instalación de ACS del ejemplo derivan en la reducción de las pérdidas globales en un 30% respecto las pérdidas de la instalación con velas sin aislar, aumentando el coste de la instalación un 58%.
Se observa como al aumentar el aislamiento en las tuberías se obtiene la disminución de pérdidas. Consecuencia directa de este fenómeno es el valor del radio crítico. Si observamos los valores de la tabla 7 y los diámetros externos de la tubería de la tabla 4, se comprueba que en todos los casos el diámetro exterior de la tubería supera el radio crítico y, por tanto, estamos en la zona donde la adición de material aislante reduce las pérdidas.
La conclusión más importante del presente artículo es que tal como se comprueba en el último caso de estudio, no se precisa ningún tipo de aislamiento en la instalación térmica de ACS para cumplir con las exigencias legales, con el importante ahorro que supone.
Dada la exigencia de aislar los conductos en recintos no calefactados se escogería aquel fabricante que posea el menor espesor en su gama de productos siempre y cuando las características térmicas sean equivalentes a las iniciales del caso de estudio para cumplir con el aislamiento establecido en locales no calefactados. O se podría instalar las conducciones horizontales empotradas dentro de los recintos calefactados.
La aplicación de la norma EN ISO 12241:2008 unido a la utilización de herramientas y modelos matemáticos de optimización, hace posible una verdadera eficiencia económica en las instalaciones que requieran aislamiento térmico sin que, por ello, se incumplan aspectos legales o medioambientales.
Por otra parte, el tiempo de resolución es mínimo, reduciéndose el tiempo improductivo dedicado a la revisión de la revisión del presupuesto para rebajar el precio final y ser adjudicatarios de la obra.
Bibliografía
Aenor (2002). UNE 92301:2002 Criterios de Medición para trabajos de aislamientos térmico de tuberías y equipos. AENOR.
BOE (2007). Real Decreto 1027/2007, de 20 de julio, por el que se aprueba el Reglamento de Instalaciones Térmicas en los Edificios. Disponible en: http://www.boe.es/boe/dias/2007/08/29/pdfs/A359 31-35984.pdf. (Consultado el 4 de julio de 2010)
CTE (2009). Código Técnico de la Edificación. Documento Básico HS 4 Suministro de agua. Disponible en: http://www.codigotecnico.org/cte/export/sites/ default/web/galerias/archivos/DB_HS_2009.pdf. (Consultado el 6 de julio de 2011).
IAPWS (2008). Revised Release on the IAPS Formulation 1985 for the Thermal Conductivity of Ordinary Water Substance.
IAPWS (2007). Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam (The revision only relates to the extension of region 5 to 50 MPa).
IAPWS (2003). Revised Release on the IAPS Formulation 1985 for the Viscosity of Ordinary Water Substance.
IDAE (2008). Soluciones de Aislamiento con Espumas Flexibles. Editorial del IDAE, Madrid. ISBN 978-84-96680-41-8
Incoprera FP (1999). Fundamentos de transferencia de calor. 4ª ed. Editorial Prentice Hall, México. ISBN 970-17-0170-4.
ISO (2008). ISO 12241:2008 Thermal insulation for building equipment and industrial installations Calculation rules.
ISO (1999) ISO 10456:1999 Building materials and products. Procedures for determining declared and design thermal values.
Massó Moreu Y (2008). El aislamiento térmico en el nuevo RITE. Revista AeI 46:22-24
Sengers JV y Kamgar-Parsi B (1984) Representative Equations for the Viscosity of Water Substance. The Journal of Physical Chemistry. Vol. 13, No. 1, 1984. Disponible en: http://www.nist.gov/data/PDFfiles /jpcrd243.pdf. (Consultado el 12 de julio de 2011).
Soriano Rull A (2008). Instalaciones de fontanería domésticas y comerciales. 2ª ed. Editorial UOC, Barcelona. ISBN 978-84-9788-715-1.