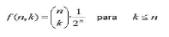Las matemáticas en los oficios y profesiones
La ciencia de los números está presente en todas las actividades laborales y profesionales y es un componente básico de la formación de cualquier ciudadano
La inventiva y a los instrumentos de medida
Ramón Sabatés inmortalizó en la figura del profesor Franz de Copenhague los denominados inventos del TBO. A menudo “los inventos” han proporcionado recursos en el desempeño de los oficios y profesiones, sin excluir las matemáticas de estos bellos retos (figura 1).
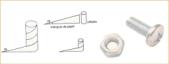
En este ámbito cabe destacar el denominado Tornillo de Arquímides, construido tal como muestra la figura 2.
La construcción anterior provoca una hélice. Cuanto más pequeño sea el ángulo del triangulo, será preciso dar más vueltas. ¿Cuánto habrá avanzado el tornillo al completar una vuelta entera el cilindro? Esta distancia se conoce como “avance”. Si el paso es de 1mm, se necesitan 10 vueltas para avanzar 1cm.
Este hecho era conocido ya por Arquímides (287-212 a. C.). El sistema fue idea do para sacar agua de un río y regar las tierras, el filete es una cuchilla en forma de helicoide de manera que al girar transporta el agua. La fabricación de pintalabios se fundamenta en este hecho. Actualmente, esta técnica se usa en carnicerías (picadoras de carne) y a nivel industrial para mover líquidos. Otras aplicaciones análogas son las hélices de un fueraborda en navegación y las hélices de los helicópteros
Seguidamente presentaremos algunos instrumentos de medida como protagonistas en numerosos oficios. Dichos elementos merecen especial atención ya que tradicionalmente han sido elementos inseparables de numerosos oficios:
Metro de cinta metálica. Es el metro por excelencia. Tiene gran exactitud y vale para tomar todo tipo de medidas. Para medir longitudes largas una persona sola, conviene que la cinta metálica sea bastante ancha sin que se doble. Suelen tener entre 3 y 5 metros.
Metro de carpintero. Se sigue utilizando en algunas carpinterías; el metro clásico de carpintero va desapareciendo poco a poco y sustituyéndose por el anterior.
Metro láser. Es el metro de última tecnología. Mide fácilmente y con una enorme precisión distancias de todo tipo. Su único inconveniente es su elevado precio para un aficionado.
Regla metálica. Las reglas metálicas son muy útiles para trabajos de carpintería por su enorme exactitud y para dibujar líneas rectas.
Escuadra de carpintero. La escuadra de carpintero es un clásico insustituible pues con ella se puede comprobar el escuadrado de un mueble (o de un ensamble) y además sirve para trazar líneas perpendiculares o a 45º respecto al canto de un tablero. Las hay regulables en ángulo.
Transportador de ángulos. Muy útil cuando tenemos que fabricar algún elemento con ángulos no rectos. También sirve para copiar un ángulo y trasladarlo al elemento que estemos fabricando.
Nivel. El nivel sirve para medir la horizontalidad o verticalidad de un elemento. Es una herramienta que no puede faltar en ningún oficio manual; se utiliza constantemente (al colgar un mueble o un cuadro, al instalar una estantería o un frente de armario, etc).
Pie de rey. Mide con precisión elementos pequeños: tornillos, orificios, pequeños objetos, etc. La precisión llega a la décima e incluso a la media décima de milímetro. Para medir exteriores se utilizan las dos patas largas, para medir interiores (por ejemplo diámetros de orificios) las dos patas pequeñas, y para medir profundidades un vástago que va saliendo por la parte trasera. Para efectuar una medición, ajustaremos el calibre al objeto a medir y lo fijaremos. La pata móvil tiene una escala graduada (10 o 20 rayas, dependiendo de la precisión). La primera raya (0) nos indicará los milímetros y la siguiente raya que coincida exactamente con una de las rayas de la escala graduada del pie nos indicará las décimas de milímetro (calibre con 10 divisiones) o las medias décimas de milímetro (calibre con 20 divisiones).
En medicina es habitual el doble decímetro usado en óptica y mide la distancia entre las pupilas.
Y en traumatología se usa un ingenioso aparato, con un transportador de ángulos incorporado, para medir desviaciones de las articulaciones.
Otro ejemplo utilizado en medicina es el análisis de los electrocardiogramas para determinar enfermedades cardiovasculares; el papel está distribuido como se indica: Voltaje: eje de ordenadas. Tiempo: eje de abscisas. Velocidad del papel 25mm/s.
Cada milímetro en las abscisas corresponde a 0,04 s y cada milivoltio se traduce en un desplazamiento de 10 mm de la aguja en el eje de ordenadas.
Algunas fórmulas de la aritmética elemental también son presentes en medicina:
El llamado índice de masa corporal (IMC) que nos indica el grado de obesidad de un paciente o la dosis de medicamento que debe tomar un niño en función de la dosis de una adulto vienen determinados por las simples fórmulas:
Algo más sofisticado es el tratamiento de tumores. Para ello es imprescindible una herramienta como la integral de superficie, estudio desarrollado en el MIT con la tecnología APA (Adaptive Phased Array)
El problema de determinar la porción del tumor que ha alcanzado ya la temperatura deseada se reduce a calcular la razón entre el volumen total del tumor y el volumen de la porción que está a temperatura mayor que la alcanzada. Este problema se resuelve usando integración múltiple.
En profesiones más técnicas aparecen elementos de criptografía, como por ejemplo la información que contienen los productos en sus códigos de barras:
“La suma de todos los dígitos que ocupan una posición impar, más tres veces la suma de todos los dígitos que ocupen una posición par (esto sólo con los doce primeros), más el dígito de control debe ser un múltiplo de 10”, como muestra ilustrativa tomemos un envase del “café solidario”;
código: 77 52063 20075 2 7+5+0+3+0+7+3(7+2+6+2+0+5)+2=90
O también los actuales sistemas de seguridad que incorporan los teléfonos móviles con el llamado código IMEI (International Mobile Equipament Identity):
En el año 2004 se han bloqueado unos 15.000 móviles, 300 de los cuales han sido desbloqueados. La solución se basa en criptografía, en el llamado código IMEI, el código de 15 dígitos que identifica cada terminal dentro de la red. Se obtiene realizando: *#06# en el terminal y aparece el número de 15 cifras. El primer bloque indica el país, el segundo el fabricante, el tercero el número de serie y el cuarto es de reserva; por ejemplo: 352167/ 40/477100/5. Cuando se inicia la conexión del teléfono móvil, la red pide siempre el IMEI antes de autorizar la llamada. En caso de incidencias es preciso indicar a la operadora el IMEI.
También destacan en los oficios las escalas logarítmicas, desde la fabricación del champú hasta los sismógrafos:
Las escalas logarítmicas se usan en algo tan cotidiano como ¡el champú! En los frascos de champú a veces se indica: “ph neutro”. ¿Qué es el ph? El ph es la concentración de iones de hidrógeno en una disolución química. El número de iones de la concentración está dado en potencias de 10: 10–1, 10–2, … 10–14. El ph es el número opuesto a ese exponente; es decir, el antilogaritmo. El ph mide el carácter ácido o básico de los jabones, lociones, champús, etc. Con ph = 7 se dice que es neutro y suele recomendarse por no ser agresivo con la piel y el cabello. Un ph inferior a 7 corresponde a una disolución ácida; si es superior a 7, es básica.
En los sismógrafos tenemos la conocida escala de Richter, si denominamos M la magnitud de un terremoto tenemos una relación del tipo:
M = logA+ 3,3 +1,6logD-logT,
donde D es la distancia entre el epicentro y el sismógrafo y T es una constante que depende del período de las ondas registradas en el sismógrafo.
Destacamos que la intensidad del terremoto es del orden de 10M, de esta manera un valor de M=6 proporciona un leve temblor del suelo al caminar y un valor de M=8 puede destruir edificios.
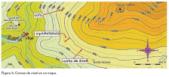
Las funciones de dos variables también están presentes en los oficios: geología, metereología, etc. Sin profundizar en el tema podemos presentar el papel de las curvas de nivel cuya interpretación, de hecho, marca el desnivel del terreno (figura 3).
1. Cota: número que indica la altura sobre el nivel del mar.
2. Equidistancia: Distancia entre cur-vas de nivel.
3. Curva de nivel: Las curvas que “tienen la misma altura”, proyectadas en el plano. Ejemplos: montañas, mapas del tiempo, etc.
Las proporciones más elementales de la escuela primaria también aparecen en “el oficio de la política”; la más destacada es la denominada Ley de Hondt (Ley electoral): La ley de Hondt establece que si “n” es el número de escaños, es preciso dividir los votos de cada coalición por 1, 2,…, n; y de los resultados obtenidos escoger los n valores más grandes
Cabe destacar que un razonamiento plausible indicaría que las abstenciones tendrían que corresponder a escaños “vacíos” en el parlamento, hecho que no sucede…..
Y hablando de proporciones, observen el tendedero modelo Drymax (figura 4).
El tendedero fue ideado por la profesora Pepita Panades y presentado a la feria internacional de inventos Galáctica 2003, minimiza el espacio y maximiza el secado. Si algún día ven en algún balcón un estendedor como el Drymax ¡les invito a contemplar la belleza del número de oro en sus articulaciones!
Homenaje a la innovación docente
Situaciones de la industria y de los oficios son un buen recurso para las aulas.
Una invitación a la modelización de situaciones reales del entorno profesional y resolución de problemas es un ejemplo brillante para introducir los bellos horizontes que la matemática nos ofrecen.
Matemáticas en los oficios
Para ilustrar una primera experiencia de innovación, mencionaré el premio María Antònia Canals a la innovación docente en matemáticas.
El primer premio M.ª Antònia Canals, en su primera edición (mayo 2003), fue otorgado a la experiencia en trabajo en proyectos realizada por Eva García Toledano del I.E.S. Salvador Dalí de El Prat de Llobregat en cuarto de ESO. El proyecto era Matemáticas en los oficios: Matemáticas del comerciante, del panadero, del pintor, del lampista, del albañil: cálculo mental, porcentajes, medidas, proporcionalidad, sistema métrico decimal. Matemáticas comerciales: albaranes, facturación, hoja de encargos, IVA, amortización de préstamos, capitalización de intereses… Para tener una ligera idea mostraré brevemente las matemáticas de un panadero cuyos contenidos presentaban: Proporcionalidad directa. Repartos proporcionales. Regla de tres simple. Sistema métrico decimal (l, dl, cl, ml, kg, g) 1. Conocer la fórmula de los diferentes tipos de productos que elaboran. 2. Saber la cantidad necesaria de cada elemento de la fórmula en función de la cantidad de producto que se desea elaborar, aplicando cálculo de proporciones. 3. Utilización de la regla de tres simple. 4. Calcular el precio de coste por unidad de producto (precio de una barra de pan, panecillo…) 5. Conocer el sistema métrico decimal (kg, g, etc.) 6. Po-seer recursos de cálculo mental rápido de precios. 7. Pagos y cambios, conocer tipos de monedas y unidades monetarias 8. Interpretación de facturas 9. En-tender la contabilidad y los costes de personal (salarios, seguridad social…), mantenimiento: luz, agua, combustible, amortización de maquinaria…. Ilustraremos el ejemplo con la fórmula de elaboración del pan: Por cada 100 kg de harina: 60 litros de agua, 2 kg de sal, 2 kg de levadura.
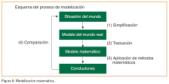
La modelización matemática es una herramienta útil para integrar las matemáticas en los currículums como forma de aproximarnos a la realidad y en particular a las profesiones y oficios. Para ello consideramos el esquema de la figura 5.
Modelizar un electrocardiogama
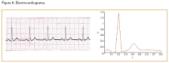
Como segunda experiencia de aula en proyectos presentamos el proyecto de modelizar la gráfica de un electrocardiograma como la de la figura 6 (véase Técnica Industrial número 256, de marzo de 2005).
El proyecto consiste en definir una función a trozos y analizar las diversas tipologías de enfermedades utilizando armónicos de Fourier. Este proyecto –realizado en grupo– se contextualiza en la especialidad de ingeniería técnica electrónica en la Escola Politècnica Superior d’Enginyeria Tècnica de Vilanova i la Geltrú (UPC) .
Un modelo obtenido con la ayuda de MAPLE es el que se muestra en la figura 7.
Usando 50 armónicos se encuentra la bella aproximación (figura 8).
Método de la solera
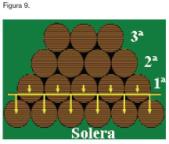
Otro hermoso modelose obtiene del problema que ilustra la figura 9: El vino más añejo está en la fila inferior de barriles y el más nuevo en el piso de más arriba. Cada año, la mitad del contenido de los barriles del suelo se embotella como jerez y se llena con vino de los barriles de la fila inmediatamente superior. El proceso se completa añadiendo vino nuevo a los barriles de la fila de más arriba. El problema es buscar un modelo matemático que nos determine la cantidad de vino de n años que se extrae de k filas de barriles (Larson,2003. Cálculo I). Los alumnos obtienen el siguiente resultado:
La aproximación del ingeniero a las matemáticas es de una naturaleza eminentemente práctica y está orientada a la resolución de problemas concretos.
Las técnicas de modelaje permiten estimular el interés por el descubrimiento y la creatividad, y adquirir confianza en las capacidades y recursos propios, destacando de esta forma el aspecto formativo de las matemáticas.
En una sociedad cada vez más influenciada por las matemáticas, mediante sus aplicaciones y modelos, es oportuno de sarrollar entre los alumnos una competencia crítica que les permita una integración en el mundo laboral y social más activa y participativa. La competencia crítica debe entenderse como una capacidad de reconocer, comprender, analizar y validar el uso de las matemáticas en el contexto real.
La capacidad de aplicar los conocimientos matemáticos que se han adquirido en las situaciones del mundo social no proviene del hecho de haber adquirido una formación abstracta sino de presentar las matemáticas relacionadas con otras áreas de conocimiento, como una actividad cultural y social (interdisciplinariedad- contextualización).
La incorporación de aplicaciones matemáticas en el currículum puede conseguir que los conceptos matemáticos tengan para el estudiante un protagonismo mental. De esta manera, la capacidad de usar un concepto matemático incluye alguna cosa más que simples conocimientos de este concepto.
Intersección regulada por semáforos
Como tercer ejemplo innovador de proyecto experimentado por los alumnos en las aulas de ingeniería electrónica de la Escola Politècnica Superior d’Enginyeria de Vilanova i la Geltrú (UPC) mostramos el caso de una intersección regulada por semáforos.
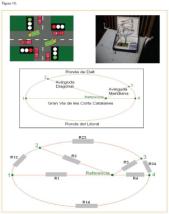
En este caso se analiza el funcionamiento de una red de circulación vial. En concreto se elige una intersección re gulada por semáforos para estudiar la evolución del tráfico, la densidad de circulación realizando mediciones experimentalmente del flujo de automóviles. En el proyecto se establece la analogía entre los elementos clásicos de la teoría de circuitos y las características del tráfico rodado: leyes de Kirchoff, teoría de grafos… y se intenta mostrar resultados como una primera aproximación al problema de la gestión del tráfico. Se escogió una intersección real y se ilustró utilizando flash de macromedia e incluso se construyó una maqueta para simular la red vial tal como ilustran las figuras 13, 14, 15 y 16.
En homenaje a los profesionales
Gracias a todos ustedes, operarios e ingenieros, por permitir que las matemáticas estén presentes en su noble tarea profesional. Sin las matemáticas no sería posible la construcción de viviendas, luz, agua, funcionamiento de aparatos electrónicos y eléctricos. Pero sólo con matemáticas tampoco; es necesaria vuestra presencia y profesionalidad. Esperemos que las matemáticas le continúen siendo útiles en el ejercicio de su profesión.
En homenaje a nuestro oficio: el noble oficio de educar matemáticamente. Y también en homenaje a nuestros maestros, y a nuestro noble oficio de educar, de ellos hemos sido aprendices. Gracias, Miguel de Guzmán; gracias, Lluís Santaló; gracias, Pedro Puig Adam; gracias, Paulo Abrantes; gracias, Esteve Terrades; gracias, George Polya; gracias a todos los lectores y maestros por la pasión por la enseñanza y vuestra labor.
Es mi deseo que los contenidos expuestos sean provechosos para enriquecer nuestra tarea y mostrar en las aulas y fuera de ellas esta hermosa visión utilitarista de la matemáticas.
Espero que con los temas expuestos pueda contribuir a “hacer visibles” las matemáticas en el entorno profesional, social y académico.
Una reflexión educativa: la metáfora del nadador
“Imagínese una escuela de natación que se dedicara un año a enseñar anatomía y fisiología de la natación, psicología del nadador, química del agua y formación de los océanos, costes unitarios de las piscinas por usuarios, sociología de la natación, antropología de la natación y, desde luego, la historia mundial de la natación, desde los egipcios hasta nuestros días. Todo esto, evidentemente, a base de cursos magistrales, libros y pizarras, pero sin agua. En una segunda etapa se llevaría a los alumnos-nadadores a observar durante varios meses a nadadores experimentados; y después de esta sólida preparación, se les lanzaría al mar, en aguas bien profundas, en un día de temporal invernal”.
(Busquet, J. ¿Pueden fabricarse profesores? En J. Busquet, (ed.): La problemática de las reformas educativas. INCIE, Madrid, 1974, p. 50)
Bibliografía
Alsina, C. Burgués, C. Fortuny. 2001. Ensenyar Matemàtiques. Graó.
Alsina, C. (2005). Geometría cotidiana. Rubes.
Bolt, Brian (1992). Matemáquinas. Edit. Labor
Bolt, B; Hobbs, D. (1991). 101 proyectos de matemáticas. Edit. Labor
Cockcroft, Informe (1985). Las matemáticas sí cuentan. MEC
Cabrara, G. (1998). Semiología del electrocardiograma, Análisis e interpretación, Ed. Grupo Aula médica.
COMAP. (2000). Matemáticas y vida cotidiana. Addison- Wesley.lGarcia,
Garcia Rafi, L. M; (1998). Proyectos de Matemática Aplicada para ingenieria. Publicaciones UPV
Gómez, J. (2002). De la enseñanza al aprendizaje de las matemáticas Edit. Paidós.
Gómez, J. Técnica Industrial. Marzo 2005
Larson (2003). Calculo I y II. Séptima Edición. Edit. Pirámide.
Puig Adam, P. Cálculo Integral. Edición 1972.
RESUMEN
El artículo se puede focalizar en el papel de la matemática en la formación de ciudadanos y ciudadanas con sentido crítico, en el contexto de los oficios que nos ofrece la sociedad del siglo XXI Podríamos preguntarnos: ¿Qué ofrecen las matemáticas en el currículum, además de rutinas y aritmética, para el uso cotidiano y en particular para el ejercicio de la profesión? ¿Cómo influye la matemática en los oficios y viceversa? Destaco la bella cita de H. Pollack: “Tradicionalmente, las matemáticas de la vida normal de cada día han sido las de la escuela primaria. Las matemáticas para ejercer una ciudadanía inteligente tendrían que ser básicamente, las matemáticas de la educación secundaria. Las matemáticas para el ejercicio profesional han de ser enseñadas en la etapa universitaria (si el ejercicio de la profesión requiere estudios de este nivel). Las matemáticas como parte de la cultura integral humana no han sido asignadas a ningún nivel educativo”. Las matemáticas han permitido a pintores pintar de forma realista, también han contribuido a la comprensión de los sonidos musicales y su análisis, las matemáticas son imprescindibles para la construcción de teléfonos móviles, radio, aparatos de grabación (dvd, cd, etc.). Las matemáticas, y en particular los modelos matemáticos, son necesarios para el avance de la biología, la economía, etc. y en síntesis imprescindibles para la tecnología actual. Los conceptos matemáticos son fruto de fenómenos reales que se encuentran cada día presentes en los oficios y en la vida cotidiana. En el texto se describen varios estadios de la matemática que han contribuido en los oficios, recogiendo la simple aritmética elemental y pasando incluso por elementos de matemática superior y su influencia en las profesiones. Es deseable que nuestros alumnos aprendan cómo las matemáticas pueden influir en su futuro profesional.