La planificación de la producción

El cálculo de las necesidades de fabricación de un producto depende de diversos parámetros que pueden integrarse en una ecuación. Aquí se aplica a la fabricación metalúrgica.
La mentalidad de las empresas en relación al sistema de producción ha cambiado considerablemente; en los años 20 la empresa tenía como objetivo conseguir un gran volumen de producción, en los 60 esta mentalidad fue madurando y se enfoca hacia la venta, dejando la producción supeditada a ella. En la actualidad y debido a la competencia existente, esta mentalidad se ha tenido que ajustar para buscar tres objetivos, fabricar la cantidad necesaria, en el plazo previsto y con la calidad demandada, todo ello para poder participar en el mercado de forma competitiva y buscando la rentabilidad.
En este artículo, no se pretende un análisis de los distintos sistemas de planificación de la producción existentes, sino del problema que se plantea en un sistema productivo industrial, que no es otro que conocer la cantidad a fabricar de cada artículo en un periodo de tiempo determinado, aprovisionando con antelación la materia prima y conjugándolo con la carga de trabajo del sistema productivo, su capacidad y los recursos de que se dispongan en ese periodo. De este problema es de donde arrancan todos los sistemas de gestión utilizados, aportando soluciones, cada uno de ellos con unas características determinadas.
El cálculo de las necesidades de fabricación de un producto depende de diversos parámetros que pueden integrarse en una ecuación. Aquí se aplica a la fabricación metalúrgica.
A la tendencia actual de fabricar la cantidad necesaria, con la calidad demandada y en el plazo previsto, hay que añadir la gran competitividad habida en todos los sectores. Hoy en día no hay grandes diferencias entre productores de un mismo producto, siendo ambos productos comparables en calidad y precio. Las diferencias se establecen en el sistema de planificación de la producción. Obtendrá ventajas quien compita con un sistema capaz de generar una información actualizada y más acertada a las necesidades.
Este objetivo es sumamente complejo, por la gran cantidad de variables que entran en juego, y por su relación antagonista, como es el caso stock frente a inversión en inmovilizado. Nos encontramos pues, ante un problema de optimización multiobjetivo y antagónico, donde la mejora de unas condiciones (determinadas variables) empeora otras. El resultado será, como en la mayoría de los problemas ingenieriles, una solución de compromiso ponderada en función de ciertas variables, es decir, dando mayor importancia o peso específico a las variables que se determinen, bien por ser las que cobren una relevancia especial en la situación actual del mercado u otra razón de peso. La filosofía japonesa de los sistemas de producción avanzados, toma como objetivo minimizar el coste utilizado, definiendo el coste utilizado como el coste asociado a las inversiones realizadas para la fabricación, por lo que trata de reducir el tiempo que transcurre entre la compra de materia prima y su entrada en el sistema de producción, o la salida del producto terminado del sistema de producción y su venta, a fin de cuentas, se trata de realizar la inversión justo en el momento necesario y mantener unos inmovilizados mínimos. Ataca pues a la cantidad y al tiempo que transcurre sin que dicha inversión aumente su valor añadido.
Resulta entonces sencillo comprender la magnitud y complejidad que presenta el problema, por lo que las soluciones deben ser muy bien estudiadas y requieren un detallado y minucioso examen para aplicarlas a los sistemas de producción, ya que cada sistema en particular tendrá una serie de características comunes a otros sistemas de producción, pero también tendrá características exclusivas que implican la elaboración de un examen exhaustivo del modelo o sistema de planificación de la producción más conveniente para el sistema y para los resultados exigidos. Además debe evaluarse la relación entre los requisitos que exige la implantación del sistema de planificación (coste, tiempo de implantación…) y las exigencias que tenemos de información, para que la elección sea ante todo rentable. La rentabilidad es la variable que debe optimizarse en toda empresa situada en un mercado altamente competitivo.
Planteamiento del problema
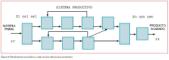
Cualquier sistema productivo puede esquematizarse en una serie de etapas productivas, que arrancan con la materia prima y concluyen con la expedición del producto terminado. En la sucesión cronológica de estas etapas podemos encontrar recirculación de productos a un punto posterior o saltos de algunas etapas. Un esquema representativo de lo anterior es el de la figura 1:
El flujo de materiales puede ser complejo, y dependerá de la familia de piezas o incluso puede ser diferente para distintos productos, lo que complica aún más la organización del sistema de producción.
Toda la información necesaria para poder controlar el sistema productivo, se introduce en el sistema de planificación para obtener los resultados oportunos y pasar posteriormente a la etapa de programación de la producción. Este sistema suele soportarse con un programa informático al que se le introducen unos datos de entrada o inputs, y mediante un análisis (que difiere según el sistema de planificación que tenga implementado) per-mite finalmente la toma de decisión de la cantidad a producir, uso de la capacidad, reparto de la carga de trabajo, etc.
La forma en la que vamos a tratar el sistema de planificación, para modelizarlo, es el de una caja negra, que recibe una información o inputs, y bajo varias
falta texto
dicionada por las restricciones que nosotros le impongamos? Ésta es la parte que se presenta a continuación y que constituye el núcleo desde el cual se debe partir para dar una solución al problema de organización y gestión de la producción desde su etapa de la planificación.
Previsión de ventas
Vamos a ir definiendo cada una de las entradas al sistema de planificación de la producción (en adelante SPP) de forma sistemática para luego formular la ecuación que gobierna el “comportamiento” del SPP. La primera entrada de la que hablamos era la previsión de ventas. Como es sabido, la previsión de ventas es el presupuesto del que parten todos los demás planes de la empresa: plan de producción, previsión de beneficios, planes de financiación, de inventario, de compras, etc., por lo que su determinación ha de ser realizada con cuidado. Aún así hemos de saber que siempre va a estar sometida a un cierto error o incertidumbre asociado a dicha previsión.
Existen en la actualidad varios métodos de previsión de ventas, basados, en general, en extrapolar los datos históricos de series de ventas pasadas al futuro. El planteamiento se expone a continuación.
Partimos de la curva de ventas de un cierto periodo, por ejemplo las ventas que se han producido en los dos últimos años (figura 4).
Observando la forma de la curva de ventas es posible detectar que siempre podemos descomponerla en tres términos; Vi = Ti + Ai +Ei ; siendo cada término:
Ti : Tendencia; es la recta cuya pendiente nos indica la evolución general de las ventas, puede obtenerse realizando un ajuste por mínimos cuadrados a la curva de ventas.
Ai : Aleatoriedad. Es la diferencia entre las ventas reales y la suma de las otras dos componentes, este error, como puede intuirse, es de naturaleza estadística.
Ei : Estacionalidad. En general, la mayoría de los artículos presentan una variación en sus ventas con el tiempo según la época del año en que nos encontremos, así, las mayores ventas de refrescos se dan durante la estación estival (en la gráfica aparece como función periódica).
Basándose en este principio de descomposición, los diferentes métodos de previsión extrapolan la tendencia pasada al ejercicio en que queremos realizar la previsión, componen a esa tendencia la curva periódica de estacionalidad y añaden a esa suma la aleatoriedad en cada periodo calculada aplicando ciertas reglas heurísticas a las aleatoriedades observadas en tiempos equivalentes de ejercicios pasados. En resumen, calculan, basándose en datos históricos, cada uno de los tres términos Ti , Ai y Ei, y por separado para luego componerlos. Fundamentados en este principio encontramos métodos como alisado exponencial, medias móviles, ajuste por mínimos cuadrados, por series de funciones periódicas, etc., en cuya descripción detallada no entraremos.
No hemos hecho mención hasta ahora a la duración del periodo de tiempo t en el que calcular la previsión. Para definirlo de forma correcta hemos de tener en cuenta el tiempo de fabricación del artículo cuya producción queremos organizar. Si este periodo es de 3 meses, es en general suficiente tener una previsión de ventas por meses. Con tiempos de fabricación menores, hemos de construir un plan de ventas por semanas, que es el caso más común. Como caso particular, existen ciertas empresas que trabajando según la filosofía JIT, con sistemas de producción basados en tarjetas Kan-Ban y alta flexibilidad productiva, disgregan las previsiones semanales en diarias, para ajustar su fabricación lo más posible a la demanda real con mínimo stock.
Después de esta breve mención a la previsión de demanda, proseguimos definiendo el modelo de SPP, con el siguiente factor en él interviniente: la producción real obtenida del proceso cuantificada por su rendimiento.
Rendimiento del proceso
En un proceso de fabricación de piezas metálicas, pueden ser varias las operaciones que se produzcan a lo largo de las secciones del mismo: moldeo, fundición, desbarbado, temple, soldadura, fresado, torneado, taladrado, estampación, embutición, repasado, electropulido, baño, etc. Cada una de estas secciones tiene un rendimiento asociado que puede definirse como:
Rendimiento de la sección i ; ?i= Nsi / Nei (1)
Siendo: Nsi = Número de piezas “buenas” que salen de la sección i.
Nei = Número total de piezas que entraron en la sección i.
Hay que notar que en realidad, de la totalidad de las piezas perdidas en la sección i, esto es, Nei – Nsi, una parte de ellas serán desechos de la sección i (piezas que se destruyen en el transcurso del proceso productivo por cualquier causa) y otra parte serán piezas rechazadas por la sección i+1 por falta de calidad, siguiendo la filosofía de cliente interno (control de calidad en cascada). Según esto, el rendimiento de cada sección se puede expresar como:
?i= ?si?ci (2)
Siendo ?si el rendimiento asociado a la sección sin contar con el control de calidad de la sección posterior (cuantifica el % de desechos de la sección i) y ?ci mide el porcentaje de piezas que “pasan” el control de calidad de la sección posterior. Considerando que en general el proceso está compuesto por N secciones, el esquema de un sistema productivo puede complicarse al haber retrocesos (figura 5).
El rendimiento de todo el proceso estará dado por
NN
? p= ?1?2K?n= ?? ?i= ?? ?si ?ci ,
i=1 i=1
siendo ?p la relación entre el número de piezas aceptables que salen del proceso y el número de piezas que entraron en el proceso, de esta forma: ?p = PR / PT; siendo PT (producción teórica) y PR (producción real).
Este último resultado es fundamental, puesto que en la planificación de este tipo de fabricaciones, hay que lanzar una producción corregida por el factor ?p , ya que en caso contrario la salida de nuestro proceso será inferior a la necesaria y podríamos caer en una situación de rotura de stocks. Pudiera parecer que esta solución elude atacar el problema del rendimiento del proceso de raíz, esto es lanzar PT sin corregir consiguiendo ?p= 1. Como
? p =?1?2K?n= ?? ?i= ?? ?si ?ci ,
i=1
entonces ?si = ?ci = 1. Para conseguir ?ci = 1, podemos aplicar las técnicas de mejora de la calidad actualmente muy desarrolladas para intentar alcanzar el objetivo de cero defectos (?ci = 1). En cuanto a ?si es más complejo hacerlo igual a la unidad, ya que según se comentó, algunos procesos de fabricación como la fundición, presentan un proceso complejo desde el punto de vista tecnológico, puesto que cualquier cambio en las condiciones, puede hacer variar el rendimiento de estos procesos, lo que lo hace difícilmente controlable.
Por otra parte no hemos considerado hasta ahora que los desechos puedan reprocesarse, en este caso, es fácil demostrar que la cantidad producida en el proceso de fabricación (desechos en cada sección y rechazos por calidad) vendrá dado por:
N i–1
DT = ?? (PT (1–?si ?ci )( ??sj ?cj )=D
i=1 j=1
=D+D2 +K+DN (3)
Suponiendo un tiempo de reproceso TRPi medio por pieza en cada sección y un porcentaje ri de desechos que pueden ser reprocesados en la seción i, tendremos una producción retrasada respecto de la producción real llamada producción por reprocesos (PRP) cuyo valor es:
N
PRP = ?? (riDi)=r1D1K rNDN (4)
i=1
Con un retraso (R) respecto a la producción real de:
N
R= ?? (rDTRP) (5)
ii i
i=1
Según esto la producción real del sistema (PR’) en un intervalo de tiempo igual al proceso de fabricación más el retraso por reprocesos será:
PR’ = PR + PRP (6)
Estando PR terminada en el plazo de fabricación y llegando PRP en el plazo de fabricación más el retraso R.
Previsión de devoluciones
Este es otro de los parámetros importantes que influyen en el sistema de planificación ya que las devoluciones han de tratarse como un recurso futuro. En otros sectores como el textil adquieren mayor importancia, no obstante, puede pensarse en el caso poco común de una fábrica de artículos de joyería que manufactura productos metalúrgicos y donde se produce un alto nivel de devoluciones (20%). Hay que tener en cuenta las siguientes consideraciones:
a) Denominamos devoluciones en un cierto tiempo t (que llamaremos DVt) al total de piezas que llegan a almacén en el periodo t y que cumplen todas las especificaciones de calidad (se pueden reingresar como producto terminado sin hacer ninguna modificación sobre ellas).
b) No se consideran las devoluciones por defectos de calidad sobre las que hay que realizar algún tipo de reproceso, sin embargo, su consideración como entrada al sistema como un desecho es la misma que la de los desechos del sistema realizada anteriormente.
El tratamiento de las devoluciones se realiza tradicionalmente representando la curva acumulada de ventas junto con la curva acumulada de devoluciones en el ejercicio anterior (figura 6).
La previsión se realiza de la forma siguiente: para prever las devoluciones que se van a producir en un cierto periodo t, aplicamos la regla sencilla:
PDt = (VRt–1 / PVt ) DRt–1 (7)
Siendo:
PDt : Previsión de devoluciones durante el periodo t.
VRt–1: Ventas reales durante el periodo equivalente a t del ejercicio pasado.
PVt: Previsión de ventas para el periodo t.
DRt–1: Devoluciones reales durante el periodo t–1.
Una vez definidos los parámetros intervinientes en el modelo, estamos en condiciones de plantear la ecuación que cuantifica su evolución temporal.
Planteamiento de la ecuación general
En este apartado vamos a obtener la ecuación que gobierna el funcionamiento de los SPP en función de cada uno de los parámetros definidos anteriormente. Partimos del principio de conservación que afirma que la variación de una propiedad de un sistema en un cierto intervalo de tiempo, es igual a la cantidad de propiedad que entra, menos la que sale del sistema, más la generada dentro de él. Para aplicar este principio al problema que nos ocupa, sólo hemos de identificar el término “propiedad” con el stock, las salidas con las ventas que se producen (PV), las entradas con las devoluciones recibidas (PD) y la generación del sistema con la cantidad de piezas producidas en el intervalo de tiempo estudiado.
Según esto, para un cierto intervalo de tiempo (t, t + 1), que puede ser una semana, un mes, etc., es posible escribir la ecuación:
St+1 – St = PDt – PVt + PRt (8)
Demostramos en el apartado anterior
?p = PRt / PTt–TF (9)
Se ha utilizado el subíndice t-TF, porque la producción teórica ha de ser lanzada con una antelación mínima de un periodo de fabricación TF respecto al tiempo en que queremos que esté terminada. Sustituyendo PRt en la ecuación anterior resulta:
St+1 – St = PDt – PV + PTt-TF ?p (10)
Siendo:
St+1 : Stock al final del periodo considerado.
St: Stock al inicio del periodo.
PDt: Previsión de devoluciones para el periodo
PVt: Previsión de ventas para el periodo.
PTt–TF: Producción teórica lanzada en el periodo t–TF (siendo TF el tiempo de fabricación del producto), y que se termina dentro del intervalo de tiempo considerado.
?p : Rendimiento del proceso.
Nuestro objetivo es obtener las necesidades de fabricación en cada periodo, para ello despejamos PTt–TF
PTt–TF = (St+1 – St– PDt+ PVt ) / ?p (11)
Obsérvese que partiendo de un stock St conocido, que puede ser cero (nueva planta de fabricación, nuevo producto), o distinto de cero; solo hace falta fijar un cierto stock St+1 al final de cada periodo para obtener las necesidades de lanzamiento en t–TF. Cuando se tengan los datos reales de ventas, devoluciones y producciones reales de cada periodo es necesario realimentar el sistema para adaptarlo al plan previsto. Hay que tener en cuenta los errores asociados a la previsión de ventas (que siempre existen a no ser que fabriquemos bajo pedido) y a la posibilidad de que se produzca un cierto retraso en la producción. Llamando a estos dos factores E y r respectivamente (medidos en % de error y % de retraso), hay que añadir a la producción teórica un cierto “colchón” para absorber estos errores que la mayoría de los autores llaman stock de seguridad y que puede expresarse como:
SSt = (E + r) PVt (12)
Con lo cual la producción teórica total a lanzar será: 
Diseñando un programa podemos simular esta última ecuación y resolver el problema de la planificación de la producción en cualquier empresa, adaptando los parámetros de la misma al SPP específico de la empresa, tema que trataremos posteriormente.
Aplicación a los distintos sistemas de organización de la producción
En la ecuación (13), el parámetro básico de decisión, es la diferencia entre los stocks al inicio y final del periodo. Es posible particularizar la expresión anterior en el caso de que nuestro sistema productivo tenga una capacidad flexible (JIT, gestión de stocks clásica) o prefijada (lotes estándar, TOC).
Just in Time (JIT)
En un sistema que opere bajo la filosofía JIT, el objetivo es producir lo que se necesita en cada momento, sin almacenar nada, en este caso haremos St+1= St = 0, con lo que las cantidades a lanzar son:

Sistema clásico de gestión de stocks
Para un sistema clásico de gestión de stocks, nuestro punto de pedido será el nivel de stock tal que quede por debajo de la venta prevista durante el tiempo de fabricación, al simular la ecuación (10) hemos de imponer la detección de esta condición y observar en qué periodos se producen estos puntos de pedido, lanzando una orden de fabricación desfasada un tiempo TF respecto a ese periodo. La cantidad de la orden de fabricación se obtiene de forma iterativa volviendo a simular el sistema con las órdenes emitidas de forma que no se produzcan más puntos de pedido y estableciendo otras restricciones como stock máximo, capacidad máxima, etc. En este caso no se simplifica ningún término de la ecuación y hemos de elegir los puntos de pedido de forma que la evolución del stock se corresponda con la estacionalidad de las ventas y que la capacidad productiva alcance el máximo equilibrio posible.
Sistema de capacidad prefijada
En este sistema se produce a una capacidad definida por periodo, bien porque producir esa cantidad es lo más económico (lote económico), por la naturaleza del suministro, por razones de economía de montaje del producto (lotes estándar), porque se ha alcanzado la capacidad máxima de fabricación, o bien debido a que el sistema productivo se ha diseñado para que todas las secciones trabajen a la capacidad que tiene el cuello de botella de la fábrica (sistema TOC), en todos los casos las piezas que se terminan en t y que hay que lanzar en el periodo t–TF son Ct (capacidad del sistema de producción en el periodo t), entonces:
St-1– St = ?pCt – PVt (1 + E+ r) + PDt (15)
En este caso ya vienen determinadas las piezas a producir en cada periodo, hay que verificar, sin embargo, si con la capacidad de producción actual se satisface o no la demanda prevista, y simular el stock previsto para ver si está sobredimensionado o no respecto a las ventas.
Resumen
La planificación y programación de la producción resuelve qué, cuándo y cuánto se debe fabricar para abastecer la cadena de distribución. Dentro de esta cadena intervienen parámetros aleatorios como ventas, devoluciones, retrasos en la fabricación, etc., que complican el problema de la planificación. Existen diversos sistemas para llevar a cabo tal planificación. Todos ellos parten del cálculo de necesidades de fabricación de producto terminado. En este artículo se obtiene una expresión general que describe el problema de generación de necesidades, y se particulariza para los distintos sistemas de planificación de la producción.
Conclusiones
En este artículo se ha estudiado la naturaleza de los parámetros que intervienen en la planificación de la producción y se ha obtenido una expresión que con carácter general deberá ser aplicada a nivel de artículo. Esta fase requiere la implementación de la ecuación en un programa informático y su conexión con un sistema gestor de base de datos donde se almacenen los valores históricos de los datos de ventas, devoluciones, producciones, etc., del cual se alimentará el pro-grama principal.
Referencias
[1] P.M. Franses, “Time Series Management for Business and Economic Forecasting”, Cambridge University Press (1998).
[2] G. E. Box, G. M. Jenkins and G. C. Reinsel, “Time Series Analysis”, Prentice-Hall (1994).
[3] E. Cornacchia, J.P. Santandreu, “Técnicas avanzadas de planificación de la cadena de reaprovisionamiento”. Instituto para el desarrollo e investigación Logística (1999).
[4]. J.L. Burbidge, “ El control de producción”, Deusto (1979).