Justificación de cálculos en instalaciones de conducción ramificadas

La justificación de sus cálculos por parte del ingeniero no es sólo un imperativo legal, sino la garantía de verificación del proyecto
Las instalaciones basadas en conducciones ramificadas abundan en la práctica profesional de un ingeniero. Se trata, entre otras, de las infraestructuras de alimentación eléctrica en polígonos residenciales e industriales, las de alumbrado público, las canalizaciones de distribución de agua potable o para riego y las conducciones de distribución de gas. La normativa obliga a diseñarlas justificando cálculos, lo que significa que en el proyecto habrán de figurar los detalles suficientes, para que un tercero pueda verificarlos, siguiendo el mismo método que el proyectista. En este artículo se trabaja a partir de la consideración de que es exigible ofrecer estos cálculos verificables y que no basta con resumir resultados, a menudo obtenidos a través de programas comerciales que no proporcionan la suficiente transparencia. Su empleo impide, en la mayoría de los casos, verificar resultados, y obliga a un tercero a calcularlos de nuevo, cuando simplemente quería realizar una comprobación.
Planteamiento del problema típico
Una instalación ramificada se diseña describiéndola suficientemente en la memoria del proyecto correspondiente, y resumiendo en ella las características principales del material que la compondrá. Ese material ha de ser calculado de forma verificable por terceros, y el habitual anejo de cálculos ha de contener los datos suficientes como para poder reconstruir el cálculo con facilidad, es decir, aplicando las fórmulas bien explicadas que se señalan a los datos que se hacen constar. El anejo de cálculos, por supuesto, ha de venir firmado por el proyectista, que es la forma legalmente pre-vista para asignar la responsabilidad sobre ellos al autor del proyecto. En este sentido hacen bien los técnicos que visan en los respectivos colegios al advertir del vicio de procedimiento que supone fir-mar solo la memoria, pues podrían plantearse dudas acerca de la responsabilidad en caso de instalaciones mal calculadas. El problema se agrava si el proyectista aduce la utilización de un programa comercial que solo ofrece resultados, esencialmente no verificables sin un nuevo cálculo desde el principio.
Las instalaciones ramificadas son particularmente fáciles de calcular empleando métodos informáticos sencillos, como una hoja de cálculo. La hoja de cálculo, impresa e incluida en el proyecto, ofrecerá todos los datos necesarios al ulterior verificador, y solo requiere una introducción adecuada que explique las fórmulas usadas en cada una de sus columnas.
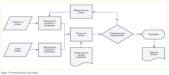
En general, una instalación ramificada, como las eléctricas, hidráulicas y gas mencionadas al principio, requiere calcular secciones de las conducciones –cables o tuberías– en función de dos variables distintas: caídas de tensión e intensidades admisibles, en el caso de las eléctricas, y pérdidas de carga y presiones en los nudos en las otras. Influyen además otros factores, que son o bien datos para el proyectista o bien resultados de criterios de diseño impuestos por la práctica o fruto de un análisis de costes y beneficios. El esquema de la figura 1 resume esta situación.
El proceso de cálculo de estas instalaciones siempre requiere analizar tramo a tramo el valor que va adquiriendo una de las dos variables, acumularlo progresivamente mientras se recorre la red “aguas abajo”, y luego analizar la otra variable acumulando sus valores en los tramos, yendo “aguas arriba”. Este doble proceso de análisis y acumulación de datos, una vez “aguas abajo” y otra “aguas arriba”, es complicado de hacer cuando la instalación está muy ramificada, pues en las confluencias de distintas ramas hay que considerar cuidadosamente la suma de todos los valores que cuelgan “aguas abajo” y, recíprocamente, al ir “aguas arriba” no se pueden mezclar datos de ramas distintas.
En los apartados que siguen se aborda, con más detalle, cómo es el anterior proceso de cálculo en una de las instalaciones mencionadas. El objetivo es mostrar cómo una moderna hoja de cálculo per-mite resolver de manera simple el problema de la doble acumulación, con tal de identificar bien los distintos tramos de la red, a la vez que constituye la manera ideal de presentar los datos de forma totalmente verificable. Este método es fácilmente aplicable a instalaciones de redes de cualquier tipo.
Cálculo de una instalación ramificada para distribución de agua
La figura 2 reproduce el esquema de una instalación hidráulica ramificada en la que los nudos son arquetas de derivación de ramales o arquetas de acometida para la toma de cada usuario, en cuyo caso les corresponde un caudal instantáneo determinado, cuyo valor se indica en m3/h.
Datos y criterios de diseño
Los criterios de diseño y los datos iniciales son los de la tabla 1. En ella también se indica qué parámetros principales y secundarios se derivan de ellos, para ser incorporados al proceso de cálculo.
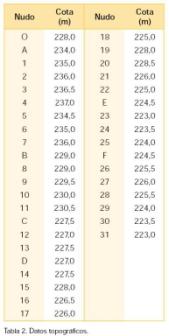
Del esquema de la figura 2, se pueden obtener las longitudes reales de los tramos Lr (m) y los caudales instantáneos teóricos por nudo Qit (m3/h). Con los datos topográficos de la tabla 2 se cuenta ya con los parámetros principales. Los secundarios, que podrán alterarse a discreción del proyectista, se resumen en la tabla 3.
Una vez determinados todos los parámetros de la instalación, se procede a incorporarlos al procedimiento de cálculo. Este ha de permitir obtener los diámetros interiores de las conducciones para lograr satisfacer las comprobaciones finales, en función de la normativa vigente o de otros criterios impuestos por el proyectista. En este caso, se fija como requisito que la presión en cualquier nudo se encuentre dentro de un rango específico:
Requisito final: 25’0 = presión mínima en cualquier nudo (mca) = 35’0.
Cálculos
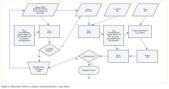
El método de cálculo exige comprobar, para cada nudo de la red, cuál es la presión resultante en las condiciones de diseño que, a su vez, dependen de los parámetros principales, secundarios, y de los diámetros hallados. El flujograma de la figura 3 ilustra las relaciones a tener en cuenta.
La fila superior representa los datos, y los rectángulos indican las operaciones siguientes:
•La velocidad en cada tramo se obtiene de la expresión que iguala el caudal con el producto de la velocidad por la sección del tramo. Para las unidades que estamos manejando resulta: 
•La pérdida de carga es:
•La cota piezométrica que cada final de tramo impone al punto de alimentación de la red –y que la diferencia de alturas puede cubrir, y si no será necesario un equipo de bombeo, como en este caso depende de la cota topográfica del nudo final, de la pérdida de carga acumulada 2 hasta él, desde el principio de la instalación y de la presión mínima que se quiera conseguir. Su expresión es: 
• Queda por obtener el caudal que circula por el tramo considerado Qtramo, y la pérdida de carga hasta el origen de la instalación Jacum. Ambos datos requieren de un proceso de sumas o acumulaciones, “aguas abajo” y “aguas arriba” respectivamente, que una simple hoja de cálculo ayuda a plantear, si se organizan los datos en una tabla similar a la de la figura 4.
La acumulación en la séptima columna (G) se consigue mediante una sencilla fórmula que se repite sistemáticamente en todas sus celdas. Por ejemplo, para la celda G3, asignada al nudo A, la fórmula sería G3 =(E3 +SUMAR. SI (Orig;B3;Q_tramo)) *F3, en la que:
E3: se refiere a la celda que contiene el caudal derivado del nudo A si este fuera una acometida.
Orig: es el nombre asignado al rango de celdas que contienen los nudos iniciales de cada tramo en el orden en que han sido descritos. Puede sustituirse por su valor A3:A39, con lo que la fórmula quedaría G3 =(E3 +SUMAR.SI (A3: A39; B3; Q_tramo)) *F3.
B3: es la celda que contiene el nudo final del tramo que se está considerando, el A en este caso.
Q_tramo: es el nombre asignado al rango de celdas que contiene el caudal acumulado de cada tramo, es decir, F3: F39. Puede ser sustituido tal cual, como antes, en la fórmula, quedando G3 =(E3 + SUMAR.SI (A3: A39; B3; F3: F39)) *F3.
F3: es la celda que contiene el coeficiente de simultaneidad asignado al tramo.
La acumulación en la decimotercera columna (M) se logra de forma totalmente análoga, aunque ahora se acumula “aguas abajo” mediante la fórmula M3 = K3 + SUMAR.SI (Final; A3; J_acum), cuyo significado es similar a la anterior.
Merece la pena destacar dos cuestiones importantes:
1. Las dos expresiones anteriores descansan en la función de hoja de cálculo SUMAR.SI, que con los usos que aquí se le han dado permite ir acumulando valores de una columna “aguas arriba” o “aguas abajo” siguiendo perfectamente la estructura ramificada de la red. Para ello solo es necesario, pero a la vez imprescindible, introducir escrupulosamente los tramos con la notación aquí seguida, es decir, numerando cada nudo de forma única –no importa si con números, con letras, o con cualquier combinación de ambos–, e indicando en una columna el nudo origen de un tramo y en otra su nudo final. La función SUMAR.SI está disponible en las hojas de cálculo habituales en ofimática al menos desde el año 1998.
2. Ambas fórmulas crean lo que suele llamarse una “referencia circular”, que es la situación en la que la fórmula de una celda hace referencia a su misma celda. Las hojas de cálculo las resuelven rápidamente iterando sucesivamente tantas veces como se indique o bien, como será en este caso, hasta que cada resultado coincida sustancialmente con el anterior. El proyectista probablemente ni llegue a advertir que tal proceso tiene lugar en su aparato cada vez que se actualizan los datos.
En la tabla 4 se reproducen las fórmulas que se asignan a cada celda de la fila 3 –asignada al tramo O-A–. Las de las demás filas son similares a las de esta.

Tabla 4. Relación de celdas y fórmulas empleadas en el ejemplo.
Por último, en la celda H3 se fuerza que el diámetro teórico resultante sea un valor comercial. Para ello se alude a la tabla 5, que figura tal cual en la hoja de este ejemplo a través de la referencia “P_carga”. Y en la celda K3 se incorporan desde esa misma tabla los datos de la pérdida de carga lineal en función de la sección y la velocidad. En concreto, el rango de cedas llamado “velocidad” es el de la fila horizontal con valores 0, 0,50, 0,80… Las celdas llamadas “P_carga” son todas las demás del recuadro inferior. Es tan solo una muestra del elevado grado de automatización que, sin perder verificabilidad, permite alcanzar una simple hoja de cálculo.
Resultados
Las celdas de la parte baja de la hoja que ha servido de ejemplo –figura 4– resumen los cálculos obtenidos. Por ejemplo, P41 y P42 son las presiones mínima y máxima, que se alcanzan en los nudos 4 y 22 respectivamente. La casilla O42 indica la presión mínima que deben dar las bombas, para satisfacer la condición anterior –36,95 mca–. Las J41 y J42 indican las velocidades mínima y máxima que alcanza el agua –0,55 y 1’91 m/s–, etc.
Alterar cualquier parámetro –cualquier dato de una celda sombreada– implica la actualización de todos los cálculos automáticamente, lo que per-mite optimizar progresivamente los cálculos con un mínimo esfuerzo. La tabla final se imprime y se incluye en el anejo de cálculos del proyecto.
Por último, una pequeña función ayudará también al recuento automatizado del material resultante. La figura 5 representa la parte de la hoja que incluye la información de la longitud de los tramos para cada sección, y ha sido obtenida sin más que repetir en cada celda la fórmula = BDSUMA (cálculos; 3; B48: B49), donde el nombre “cálculos” se refiere a las celdas A1: P39 de la figura 4.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | |
| 48 | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | 0 mm | |
| 49 | 0mm nom | 32 | 40 | 50 | 63 | 75 | 90 | 110 | 125 | 140 | 160 | 200 | 250 | 300 | 350 | 450 |
| 50 | L (m) | 80 | 75 | 268 | 140 | 171 | 175 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 51 | Collarines | 5 | 4 | 12 | 5 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
La fila “collarines” clasifica los collarines para derivar las acometidas en función de la sección del ramal en que irán instalados. Le corresponde la fórmula = BDCONTAR (cálculos; 5; B48: B49).
Introduciendo esta hoja de cálculo en un ordenador puede comprobarse que si los diámetros asignados coincidiesen con los teóricos de cálculo, la presión en el nudo B sería de 41’38 mca, solicitándose a las bombas una presión de salida de 49,30 mca, pero aumentando convenientemente las secciones se reducen ambos valores, como se ilustra. También puede verse rápidamente cómo influyen distintos coeficientes de simultaneidad en cada tramo. O cómo al reducir la velocidad máxima en las conducciones resulta menor presión de salida de las bombas, aunque ello requiere aumentar considerablemente todas las secciones. Y que el mismo efecto puede conseguirse manteniendo la velocidad e incrementando solo las secciones en los puntos de mayor pérdida de carga, etc.
Conclusiones
El diseño optimizado de las instalaciones concebidas como redes ramificadas requiere una gran cantidad de operaciones que es fácil sistematizar y presentar en un proyecto mediante una hoja de cálculo. Así se cumplen los mandatos de la legislación aplicable que, en general, obliga a “justificar cálculos”. Eso solo puede significar, de acuerdo con la interpretación lógica de dicha expresión, que los datos presentados deben ser “verificables”. En este ejemplo hemos querido poner de manifiesto cómo se puede cumplir con este objetivo automatizando al máximo el proceso de cálculo, sin que el proyectista pierda el control de lo que está haciendo por la ingerencia de programas comerciales no suficientemente transparentes. La hoja de cálculo, junto a una pequeña introducción que aclare el significado de sus filas y columnas, es clara y muestra todos los pasos seguidos. Sus datos y los cálculos son, por supuesto, verificables inmediatamente, lo que equivale a decir que quedan justificados.
El proyectista que haga y muestre todos sus cálculos en una hoja adquiere pleno control de la situación, y con total conocimiento de lo que está haciendo llegará sin duda a optimizar la solución, incrementando su satisfacción a medida que se acerca a ella. Además podrá, llegado el caso, discutir con seguridad cualquier opinión –porque será difícil que esté más fundada que la suya– y, por añadidura, demostrará que su solución es plenamente verificable en cualquier momento, sin necesidad de disponer de aparatos fuera del alcance de la mayoría de proyectistas ni de programas especiales. Es responsabilidad del ingeniero, asumida con su firma en el anejo de cálculos, cumplir con este estricto requisito de verificabilidad en todas ocasiones.
Bibliografía
Aenor, Sistemas de canalización y conducción de de agua en materiales plásticos, cd-rom, 2002.
A. Aznar Carrasco, Técnica de aguas. Problemática y tratamiento, 2000 (3ª edición revisada y ampliada).
E. Cabrera y A. F. Vela, Mejora del rendimiento y de la fiabilidad en sistemas de distribución de agua, 1995.
D. Escribá Bonafé, Hidráulica para ingenieros, 1988.
J. Mª Mayol Mallorquí, Tuberías, tomo III: Economía de las instalaciones, Montajes, Anexos y Tablas, 1993.
M. Mateos de Vicente, Elementos de hidráulica práctica, 1997.
Ministerio de Fomento, Normas tecnológicas de la edificación: NTE-IFA Abastecimiento, 1976.
Ministerio de Fomento, Pliego de prescripciones técnicas generales para tuberías de abastecimiento de agua, serie: Normativa técnica en la construcción, 1982, 6ª Reimpresión 2000.
¿Qué significa justificar cálculos?
La normativa actual no define de una sola manera cómo deben ser los cálculos de los proyectos. Algunos ejemplos son:
•El nuevo reglamento electrotécnico para baja tensión requiere que en un proyecto figuren los «cálculos justificativos del diseño» –art. 2.1 ITC-BT-04–.
•La norma tecnológica sobre redes para abastecimiento de agua –NTE-IFA 1976– es esencialmente un conjunto de cálculos plasmados de forma totalmente verificable.
•La norma básica de acciones en la edificación exige un elevado grado de minuciosidad al justificar los parámetros incluidos en los cálculos –art. 1.2 NBE-AE-88–, y la normativa sobre estructuras requiere que los cálculos puedan ser desarrollados por una tercera persona –art. 1.1 NBE-EA-95– o bien que su contenido y presentación sean tales que puedan reproducirse por terceros –art. 4.2.2 EHE-99–.
•Sobre condiciones térmicas de los edificios, es preciso justificar el cálculo de los coeficientes básicos –art.21 NBE-CT-79– e incluir el detalle del cálculo de las cargas térmicas, redes de conductos y redes de tuberías, todo en tablas, indicando de forma inequívoca las magnitudes, parámetros, etc., a los que se refieran los valores que figuren en sus filas y columnas así como las unidades correspondientes –RITE ITC-07 apéndice 07.1–.
Justificar es probar algo de manera convincente, en este caso mediante documentos. Por tanto, no son admisibles los meros resúmenes de cálculos, sino vienen suficientemente detallados y acompañados de la explicación que permita su reproducción por un tercero. Eso los convierte en totalmente verificables.
RESUMEN
La legislación industrial exige al proyectista justificar sus cálculos, de forma que la responsabilidad que adquiere con su firma alcance también a ellos y no solo al resultado. Pero justificar cálculos no puede significar resumir datos obtenidos a través de procedimientos no del todo transparentes, como tampoco puede valer la mera indicación del programa informático utilizado. Al contrario, los cálculos han de ser verificables, lo que exige plasmar en el proyecto no solo los parámetros de partida y de diseño, sino el procedimiento seguido y los datos intermedios, para que un tercero pueda comprobarlos y llegar al resultado sin necesidad de calcular todo de nuevo. En este artículo se tratan, como ejemplo –desde este planteamiento de verificabilidad de cálculos– las instalaciones basadas en conducciones ramificadas.