Implementación de reguladores con lógica fuzzy

Implementation of regulators using fuzzy logic

RESUMEN

La lógica fuzzy se utiliza para la resolución de una variedad de problemas, principalmente los relacionados con control de procesos industriales complejos y sistemas de decisión en general. Los sistemas basados en lógica fuzzy imitan la forma en que toman decisiones los humanos, con la ventaja de ser mucho más rápidos. En este artículo se muestra la metodología y el procedimiento de trabajo para la implementación de reguladores con lógica fuzzy, que, a diferencia de los reguladores convencionales, utilizan el conocimiento experto en lugar de ecuaciones diferenciales para describir un sistema.

Palabras clave
Inteligencia artificial, lógica difusa, regulador PID, software, sistemas expertos, control de procesos.

ABSTRACT

Fuzzy logic is used to solve a variety of problems, mainly related to the control of complex industrial processes and decision making in general. Systems based on fuzzy logic imitate the human decision making process, but with the advantage of being much faster. This article details the methodology and the working procedure for the implementation of regulators using fuzzy logic which, in contrast to conventional controllers, use expert knowledge instead of differential equations to describe a system.

Keywords
Artificial intelligence, diffuse logic, PID controller, software, expert systems, process control.

Introducción

Procedente del inglés, el término fuzzy se ha venido traduciendo como difuso o borroso. En un primer acercamiento, la lógica borrosa puede ser contemplada en contraposición a la lógica clásica. Esta última establece que cualquier enunciado o proposición puede tomar un valor lógico verdadero o falso, en definitiva 1 o 0 (parece evidente pensar que una puerta está abierta o está cerrada).

Sin embargo, en el año 1965, la aparición de un trabajo del soviético Lotfi Zadeh sobre La Teoría de los Conjuntos Borrosos, revolucionó la matemática al proponer una nueva lógica según la cual una puerta no tiene por qué estar necesariamente abierta (1) o cerrada (0), sino que puede estar abierta a medias (0,5), bastante abierta (0,8), casi cerrada (0,1), etcétera.

Paralelamente, algunos investigadores se han inclinado por la lógica difusa en problemas ciertamente difíciles. Así, en 1975, en Londres, el profesor Mandani desarrolló una estrategia para el control de los procedimientos y presentó los resultados más esperanzadores que se han obtenido sobre la conducción de un motor de vapor. En 1978, la sociedad danesa F. L. Smidth realizó el control de un horno de cemento, y esta fue la primera aplicación real industrial de la lógica difusa.

La lógica borrosa conoce su verdadero desarrollo en Japón, donde la búsqueda no es solamente teórica, sino más aplicativa, y se produjo un boom a finales de la década de 1980. La principal ventaja de utilizar términos lingüísticos es que per-mite plantear el problema en los mismos términos en los que lo haría un experto humano.

La lógica borrosa surge como un intento de formalización del razonamiento con incertidumbre. En particular, y al contrario que otras formas de razonamiento, intenta abordar problemas definidos en términos lingüísticos y, por tanto, imprecisos, en los que los datos están expresados en términos cualitativos.

El primer punto que hay que tener en cuenta al abordar el tema es el de la representación matemática de las expresiones lingüísticas. Se puede afirmar que un hombre es alto cuando mide 1,90. Evidentemente, una estatura de 1,75 ya no correspondería a un hombre alto, sino a uno de estatura normal. De esta forma, se consideraría que «1,90 es alto» es cierto al 100%, mientras que «1,75 es alto» es cierto al 0%, pero «1,75 es normal» es cierto al 100%. Pues bien, la aplicación de la lógica borrosa consiste en asignar a estaturas comprendidas entre 1,75 y 1,90, valores borrosos entre 0 y 1, de manera que «1,80 es alto» sería cierto al 33% (haciendo una interpolación de forma lineal).

Teoría de los conjuntos borrosos

En la teoría clásica de conjuntos, un elemento cualquiera pertenece a un conjunto o no pertenece al mismo, mientras que en la teoría borrosa, un elemento siempre pertenece en cierto grado a un conjunto, pero nunca pertenece del todo al mismo.

Un conjunto difuso está definido por su función de pertenencia, que equivaldría a una función característica en lógica clásica. Una función de pertenencia puede definirse como una función que crea una correspondencia para cada punto del grupo difuso A con el intervalo real (0,0, 1,0) de tal manera que m(A(x)) es una aproximación del grado de pertenencia de x en A.

El grado de pertenencia representa un grado de posibilidad de que cierta condición sea cierta. Siguiendo con el ejemplo de las estaturas, se representan en la siguiente figura las funciones de pertenencia de distintos conjuntos. Por ejemplo, la función de pertenencia del conjunto «muy bajo» se ha tomado como:

Si x ≤ 1,50 m m(x)=1

Si 1,50 ≤ x ≤ 1,60 m m(x)=1-10(x-1,5)

Si x ³≥1,60 m m(x)=0

Los conjuntos clásicos se pueden considerar un caso particular de los conjuntos borrosos, en los que la función de pertenencia toma exclusivamente valores 0 o 1. En particular, el conjunto vacío será aquel cuya función de pertenencia sea constante e igual a cero y el conjunto completo, el que tiene función de pertenencia constante e igual a 1.

Semántica borrosa

Llegados a este punto, conviene definir algunos conceptos que se emplean con frecuencia. Se denomina universo del discurso al conjunto de posibles valores que pueden tomar las variables que intervienen en el predicado (condición). En el eje de abscisas del ejemplo de la figura anterior, se representa el universo de discurso, es decir, el rango de variación de la variable estatura, que se ha escogido entre 1,50 y 2,00 m.

Se denominan etiquetas lingüísticas los valores semánticos correspondientes a un predicado. En el ejemplo, se han tomado cinco etiquetas lingüísticas, que se corresponden en gran medida con el lenguaje natural.

Las funciones de pertenencia de un término lingüístico son las que aparecen en la figura anterior. Cada término lingüístico corresponde a un subconjunto borroso que lleva asociada una función de pertenencia; esta representa el grado de asociación de un valor numérico con ese término. Por ejemplo, y como ya se dijo antes, «1,80 es alto» toma el valor 0,33.

Operadores lógicos

Estos operadores permiten escribir unas combinaciones lógicas entre nociones difusas. Es decir, hacer unos cálculos sobre unos grados de verdad. Igual que en la lógica clásica, se pueden definir unos operadores de unión (OR), intersección (AND) y negación (NOT), de la siguiente forma:

A OR B = MAX[m(A(x)),m(B(x))]

A AND B = MIN[m(A(x)),m(B(x))]

NOT A = 1-m(A(x))

Reglas difusas

La finalidad de la lógica difusa es tener en cuenta y poner en práctica la manera de razonar de un ser humano, y la herramienta más utilizada en las aplicaciones de lógica difusa es la base de reglas difusas.

Una base de reglas difusas está compuesta de reglas que suelen ser utilizadas en paralelo, pero que pueden, igualmente, estar encadenadas en ciertas aplicaciones.

Una regla es de tipo: SI {predicado} ENTONCES {conclusión}.

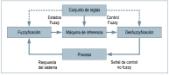
Como se puede apreciar en la figura anterior, una regla difusa se compone de tres etapas funcionales.

Predicado

Un predicado, también llamado premisa o condición, es una combinación de proposiciones para los operadores OR, AND y NOT.

Inferencia

El mecanismo de inferencia más comúnmente utilizado se denomina «de Mandani» y comprende cinco etapas:

1. Fuzzyficación: consiste en evaluar las funciones de pertenencia utilizadas en los predicados de las reglas.

2. Grado de activación: evaluación del predicado de cada regla por combinación lógica de las proposiciones del predicado.

3. Implicación: el grado de activación de la regla permite determinar la conclusión de la misma.

4. Asociación: el conjunto difuso global de salidas está compuesto por la asociación de los conjuntos difusos obtenidos por cada una de las reglas concernientes a esta salida.

5. Desfuzzyficación: al final de la inferencia, es necesario pasar del mundo difuso al real, ya que el conjunto difuso de salidas está determinado pero no es directamente utilizable para dar una información precisa al operador.

Conclusión

Es una combinación de proposiciones unidas por unos operadores AND. No se utiliza la cláusula OR en las conclusiones, ya que introducen una incertidumbre en el conocimiento.

Reguladores lógicos difusos

Los reguladores borrosos son la aplicación más importante de la teoría borrosa. Trabajan de forma algo diferente a los reguladores convencionales, ya que se utiliza el conocimiento experto en lugar de ecuaciones diferenciales para describir un sistema. Este conocimiento se puede expresar de manera muy natural usando las variables lingüísticas, que son descritas por los conjuntos borrosos.

Estructura

Un controlador borroso es un sistema basado en información imprecisa, que utiliza la teoría de conjuntos y la lógica borrosa para la representación e inferencia de ese conocimiento. Se basa en la descripción lingüística de la estrategia de control que utilizaría un operario o experto en el control manual del proceso. Por esta razón, también se denominan controladores lingüísticos.

El problema de diseño de sistemas de control se suele reducir a la elección de un determinado controlador y al ajuste de sus parámetros, de tal forma que se verifiquen ciertas especificaciones dadas para el proceso que hay que controlar. Uno de los problemas fundamentales que se plantean desde el punto de vista práctico es que no existen procedimientos sistemáticos que permitan calibrar el regulador.

El control lógico difuso funciona básicamente, tal como se puede observar en la figura 7, de la siguiente forma:

Cada variable numérica de entrada se interpreta primero en una interfase de fuzzyficación, etapa en la cual se obtienen los equivalentes lingüísticos de las variables numéricas de entrada, es decir, consiste en calcular el grado de pertenencia de las variables de entrada a cada una de las etiquetas lingüísticas mediante las funciones de pertenencia. Este será un número comprendido entre 0 y 1 para cada etiqueta.

Luego, la máquina de inferencia aplica los datos fuzzyficados de entrada al con-junto de reglas. Se hace una selección de las reglas que van a ser aplicadas, eliminando las que tengan un grado de pertenencia demasiado pequeño ya que, de no ser eliminadas, esto implicaría una acción de control contraria a la deseada.

La acción de control que concluye cada regla es un conjunto borroso al que se le ha asignado un peso. La interpretación usual de este conjunto con peso es otro conjunto borroso en el que la función de pertenencia se calcula como el producto de la función de pertenencia primitiva por el peso. Por tanto, el resultado final de la aplicación de todas las reglas es un conjunto de conjuntos borrosos con sus respectivas funciones de pertenencia.

Finalmente, como la salida del proceso debe ser también un número, se pro-cede a la interfase de desfuzzyficación, encargada de calcular el valor numérico de la conclusión a partir del conjunto de curvas de salida.

Diseño

Lamentablemente, no existe un procedimiento estándar para diseñar el controlador, pero es posible definir ciertos pasos de trabajo para llegar a un buen diseño. La metodología propuesta se resume en los siguientes pasos.

Selección de las variables y del universo de discurso

Como en todo lazo de control, el primer paso en su diseño es especificar claramente cuáles serán las variables de entrada y salida que se desean relacionar a través del controlador. Este puede desarrollarse en función del conocimiento de un experto humano, en cuyo caso esta etapa se completa rápidamente a partir de la experiencia previa. Si, en cambio, es la primera aproximación que se tiene del problema, habrá que elegir las variables que incidan directamente sobre la variable controlada, trabajando generalmente sobre el error o alguna función del error.

Selección de la estrategia de fuzzyficación

En esta etapa se determina en qué grado pertenecen las variables de entrada a los conjuntos difusos a través de su función de pertenencia. Es decir, se trata de desarrollar un bloque que tendrá en sus entradas los valores numéricos elegidos en la etapa anterior y a su salida dichos valores asociados a conjuntos difusos con sus correspondientes funciones de pertenencia. Para ello, es necesario definir estos conjuntos o universo de discurso, en un procedimiento que se conoce como particionamiento del universo de discurso, que, obviamente, requiere de un conocimiento a priori sobre el proceso que se va a controlar.

La cantidad de conjuntos difusos de nuestro universo de discurso es también una decisión de diseño. Cuantos más se elijan, mayor poder descriptivo y flexibilidad tendrá nuestro lenguaje, pues no se ha de olvidar que estos conjuntos difusos son directamente las etiquetas lingüísticas con que es necesario referirse a las variables de entrada y de salida. Por supuesto, este mayor poder descriptivo tiene su costo en mayor complejidad por la cantidad de reglas involucradas, que crece de forma proporcional. En la práctica se suelen elegir entre 2 y 10 etiquetas lingüísticas para cada variable de entrada o salida después de un procedimiento de ensayo-error.

Respecto de la forma que tendrán las funciones de pertenencia, no existen diferencias apreciables en los resultados de control entre las diferentes posibilidades.

Construcción de la base de reglas

Ya se vio que el conocimiento del controlador se almacenaba en forma de reglas que se combinaban entre sí para formar un único conjunto difuso de salida. En este apartado se mostrarán las diferentes alternativas para obtener dichas reglas, que es el punto más importante de la programación del controlador lógico difuso.

– Basadas en la experiencia y el conocimiento de un ingeniero de control experto en el proceso a controlar. El procedimiento aplicable en este caso puede ser bien un manual de instrucciones del propio experto, o bien un interrogatorio guiado, hecho por alguien que también conozca el proceso que se va a controlar, que actuará como ingeniero de conocimiento.

– Basadas en la observación de un operario experto. Existen muchas situaciones de control en las que es muy difícil hallar un modelo por la cantidad y complejidad de variables involucradas. Esto hace impensable la aplicación de una técnica de control convencional. Sin embargo, existen operarios capaces de llevar adelante el control del proceso.

– Basadas en un modelo difuso del proceso. Es posible hacer una descripción lingüística no sólo de la estrategia de control, sino también de las características dinámicas del proceso que se va a controlar. En términos generales, es un modelo difuso del proceso. A partir de este modelo se pueden obtener las reglas difusas para controlarlo.

– Basadas en aprendizaje. Su precursor fue el profesor Mandani, con el controlador autoorganizado, que está formado por dos cuerpos de reglas. Uno hace el control propiamente dicho, y el otro, a un nivel superior de aquel, exhibe el comportamiento que seguiría un programador humano mejorando las reglas de control.

– Basadas en el plano de fase. Cuando se dispone de poca experiencia previa con el proceso que controlar, esta metodología suele ser de gran utilidad porque permite, por una parte conocer el proceso en cuestión y, por otra, obtener una ley de control a partir de ideas intuitivas.

Selección de la estrategia de desfuzzyficación

Una vez cumplidas todas las etapas, el resultado de la agregación de las reglas de la base, es decir, la inferencia, será también un conjunto difuso. Sin embargo, para manejar el actuador es necesaria una magnitud no difusa. Por tanto, se necesita un bloque que sea capaz de dar una salida determinada frente a una entrada difusa y que represente lo mejor posible la distribución de posibilidades de la acción de control inferida. Para desarrollar este bloque, las estrategias más comúnmente empleadas son las siguientes.

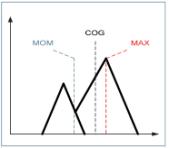
Criterio del máximo (MAX)

Es el valor del conjunto difuso de salida para el cual la función de pertenencia tiene un máximo valor. Suele tener el inconveniente de que puede dar más de un máximo, por lo que el valor final de salida del controlador no queda unívocamente fijado.

Criterio del medio de máximo (MOM)

Genera una acción de control u₀ que representa el valor medio de las acciones de control cuya función de pertenencia tenga un máximo. Es el criterio que da el mejor comportamiento en el transitorio de la respuesta. Sin embargo, posee la desventaja de no tener en cuenta la forma de las funciones de pertenencia de la salida. Esta información que se pierde tiene en cuenta parte del conocimiento obtenido en cada regla y puede resultar necesaria a la hora de obtener una respuesta.

Criterio del centro de gravedad (COG)

Genera el centro de gravedad del conjunto difuso de salida y toma este valor como salida del controlador lógico difuso. Con ello, se asegura encontrar un único valor de salida.

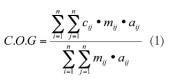
Es la opción que más información tiene en cuenta. El centro de gravedad se calcula como:

siendo cij la media, mij el paso y aij el área de la función de pertenencia asociada a la conclusión de cada regla. Como observación interesante, en el resultado final sólo influye el área y no la forma de la curva.

Autosintonía de controladores lógicos difusos

Uno de los problemas fundamentales, desde el punto de vista práctico, que se plantean a los reguladores borrosos es que no existen métodos sistemáticos que permitan calibrarlos. Partiendo de la equivalencia bajo ciertas restricciones de una determinada clase sencilla de controladores borrosos con el regulador PID, se aplican algunas técnicas clásicas de sintonía de los reguladores convencionales a los controladores borrosos para ajustar sus parámetros, considerando desde el punto de vista externo el controlador borroso un PID al que se puede aplicar todo un amplio abanico de métodos de autosintonía.

A partir de las fórmulas de sintonía de un regulador clásico (PID) se deducen las ganancias de las variables del controlador borroso, para que se comporte como un PID equivalente. Estas ganancias van en función del tiempo, ya que se parte de unos valores fijos de K_p, K_i y K_d y dependen del error y del cambio del mismo.

Además, dependen de un número elevado de parámetros. Para evitarlo, se fijan algunos de los que pueden resultar redundantes o equivalentes u otros que contribuyan a la robustez del controlador (desde el punto de vista de su estabilidad). Estos factores son parámetros críticos en el desarrollo de un controlador borroso, ya que tienen una influencia decisiva sobre la respuesta del sistema.

Con este primer ajuste analítico se obtienen unos parámetros próximos a los óptimos. Una comprensión cualitativa de la influencia de estos factores permite afinar la elección para mejorar la respuesta del sistema.

Variación cualitativa de las funciones de pertenencia

Aumentando las ganancias de las variables de entrada se comprimen las medias o centro de cada función de pertenencia de las variables de entrada, lo que supone reducir el universo de discurso, es decir, tener en cuenta valores más pequeños para la entrada del regulador y, por tanto, aumentar la resolución del control. Si no se varía ningún otro parámetro, la acción de control es más rápida y brusca, lo que mejora la respuesta transitoria del sistema disminuyendo tanto el tiempo de subida como el de establecimiento. Por el contrario, disminuir estos factores de entrada hace más lenta la respuesta.

También se consigue aumentar el grado de pertenencia de las variables aumentando la amplitud de las funciones o variando su forma. Al aumentar la amplitud, las funciones de pertenencia son más planas, por lo que cualquier valor numérico pertenecerá, en mayor medida a todas las etiquetas lingüísticas. El resultado es una acción de control más suave, ya que todas las reglas adquieren más peso y el regulador se enlentece.

Por el contrario, al disminuir la amplitud, las acciones de control son más precisas y rápidas, pues el regulador selecciona más las reglas que aplica. Pero si se disminuye demasiado, las acciones de control se vuelven irregulares, ya que quedan espacios muertos entre las funciones de pertenencia de las etiquetas lingüísticas. Por tanto, no es un parámetro que deba cambiarse en funcionamiento normal del regulador.

Variación cualitativa de la tabla de reglas

Variando las ganancias que modifican las variables de entrada y salida se consigue ajustar la acción de control dentro de ciertos límites, sin necesidad de cambiar la definición de reglas o conjuntos borrosos.

El mismo resultado puede obtenerse utilizando dos tablas, una inicial y otra de control fino, con mayor escala de resolución y acciones proporcionales a esa escala. De esta forma, un error que pudiera parecer pequeño con la tabla inicial, con esta última sería mayor y el regulador seguiría actuando, en lugar de detenerse por haber alcanzado ya la zona muerta (donde no se genera acción de control ante entradas inferiores a un límite).

Aplicación de la lógica difusa en una lavadora

Introducción

Generalmente, se selecciona el tiempo de lavado de una lavadora en función de la cantidad de ropa que se desea lavar y del grado y tipo de suciedad que tenga ésta. Para automatizar el proceso, se usan sensores que detectan estos parámetros y con estos datos se determina el tiempo de lavado.

Desafortunadamente, no es fácil formular una relación matemática precisa entre la cantidad de ropa, la suciedad y el tiempo de lavado requerido, es decir, las lavadoras no son tan automáticas como deberían.

Para construir una lavadora que sea capaz de determinar el tiempo de lavado hay que centrarse en dos subsistemas de la misma: los sensores y la unidad de control, y esta última es la responsable de tomar una decisión acerca del tiempo de lavado, pero como la relación entre la entrada y la salida no está clara, no se podrán usar métodos convencionales de control, por tanto, se ha escogido la lógica difusa.

Variables

La siguiente figura muestra un diagrama del controlador lógico difuso, el cual consta de dos entradas, una para el grado de suciedad de la ropa y otra para el tipo de suciedad de la misma. Estas señales de control se obtienen mediante un simple sensor óptico.

El grado de suciedad se determina por la transparencia del agua de lavado, ya que la suciedad de la ropa disminuye la transparencia de una cantidad fija de agua. Por otro lado, el tipo de suciedad se determina por el tiempo que tarda en alcanzar la saturación, entendiendo por saturación el punto en el que la transparencia del agua es cercana a cero, es decir, deja de ser transparente.

Funciones de pertenencia

Antes de diseñar el controlador hay que determinar el rango de los posibles valores de las variables de entrada y salida. Para ello, se usarán las funciones de pertenencia que convierten los valores reales en valores fuzzy y viceversa. Las siguientes figuras muestran las etiquetas de las variables de entrada y salida y su asociación con las funciones de pertenencia.

Los valores de las variables de entrada grado de suciedad y tipo de suciedad se han normalizado (rango de 0 a 100) bajo el dominio de los sensores ópticos.

Se han utilizado singletones (impulsos difusos) como funciones de pertenencia de la variable de salida tiempo de lavado. Como aparece representado en la siguiente figura:

Reglas

Las decisiones del controlador fuzzy se codifican mediante un juego de reglas. En general, son intuitivas y fáciles de entender, ya que se trata de sentencias «Si-entonces». Las reglas de este controlador en concreto han derivado del sentido común, como por ejemplo:

«Si el tiempo de saturación es largo y la transparencia es mala, entonces el tiempo de lavado debe ser largo».

Con diferentes combinaciones de éstas y otras condiciones, se escriben las reglas necesarias para implementar el controlador de la lavadora.

Unidad de inferencia difusa

Esta es la unidad fundamental que codifica la información del controlador. Incluye las definiciones de las variables de entrada y salida, así como las reglas de aplicación.

La figura anterior muestra la respuesta superficial de la relación entrada-salida del controlador difuso de una lavadora, determinada por esta unidad de inferencia.

El proceso de diseño de este controlador imita la intuición humana. Aunque en este ejemplo sólo se controla el tiempo de lavado de la lavadora, el proceso de diseño puede extenderse sin complicación a otras variables de control, tales como el nivel de agua y la velocidad de giro, y la formulación e implementación de las reglas y funciones de pertenencia son similares a las mostradas para el tiempo de lavado.

Figura 5. Diagrama de controlador para control de grado de suciedad.

Figura 6. Ejemplos de funciones de pertenencia.

Control difuso de flujo de fluidos en una estación de laboratorio

Los mexicanos Castro-Montoya, de la Universidad Michoacana de San Nicolás de Hidalgo, y Vera-Monterrosas y Quintana-Silva, del Instituto Tecnológico de Orizaba, han diseñado e implementado un controlador electrónico basado en lógica difusa para regular el flujo en una estación de trabajo de laboratorio.

Introducción

Utilizando su experiencia y conocimiento para caracterizar el comportamiento del sistema, formularon reglas difusas que describen las metas de control en términos de la relación de las entradas, simularon y depuraron el diseño, para, posterior-mente, implantarlo en el lazo de control de flujo de la estación de trabajo.

Figura 7. Singletones como funciones de pertenencia.

Figura 8. Respuesta superficial de la relación entrada-salida del controlador.

Para llevar a cabo la implantación del controlador lógico difuso, diseñaron y construyeron un módulo o estación de control de procesos denominado ECP2000, el cual facilita la integración de las funciones de control mediante interfases gráficas estándar hombre-máquina. El proceso consiste en el transporte de fluido a través de tuberías.

Metodología

Para el diseño e implantación del controlador lógico difuso se siguieron las siguientes etapas:

– Definición de las variables difusas y conjuntos difusos para expresar las observaciones del proceso en el lenguaje lingüístico de la lógica difusa.

– Diseño de la base de reglas difusas, basadas en los operadores y expertos en el proceso que utilizar. Se escribieron primero las reglas obvias y, posteriormente, las restantes.

– Edición de los puntos anteriores (estrategia de control difuso) utilizando la herramienta de lógica difusa de MATLAB. Guardar la unidad de inferencia difusa en la hoja de trabajo de MATLAB para generar su bloque en Simulink posteriormente.

Optimización del sistema sintonizando las reglas y/o modificando los con-juntos de entrada/salida para lograr la estabilidad y la adaptabilidad del proceso. Se utiliza la herramienta Simulink de MATLAB junto con los bloques de entrada/salida de la ECP2000.

Variables, conjuntos y reglas difusas

La definición de variables consiste en establecer los rangos (universo de discurso) de cada una de las variables de entrada y salida en unidades de ingeniería, además de definir el número de funciones de pertenencia o conjuntos difusos de las mismas. No existe una regla para definir el número de funciones de membresía, sólo la experiencia y el análisis de la respuesta de control deseada darán la pauta para esta elección.

Uno de los objetivos de control es la adaptabilidad del sistema, por lo cual se decide utilizar una entrada como la referencia y así el sistema de control difuso puede tener un mejor seguimiento de tal variable. Se utilizan las variables de error y cambio de la variable medida, como señales de entrada obvias que tienen que ver con el comportamiento transitorio y la estabilidad del sistema. Como variable de control, una señal de salida de 4 a 20 mA que gobierna el elemento final de control (bomba centrífuga).

La definición de los conjuntos difusos, es la visión del universo de discurso de la variable en regiones geométricas. Estas pueden tener forma triangular, trapezoidal, singleton (impulso difuso) o gaussiana, entre otras, y deben ser identificadas con nombres difusos.

Para este sistema se proponen 35 reglas difusas de un total de 900 posibles.

Esquemas de control

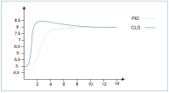
Con el objeto de comparar el comportamiento en lazo cerrado de un controlador PID con el controlador lógico difuso ante cambios en la referencia y señales de perturbación, el controlador PID se sintonizó bajo el método de respuesta transitoria (Ziegler-Nichols); posteriormente, se realizó una sintonía fina en línea, de modo que el sistema de lazo cerrado no exhiba un sobrepico demasiado alto y, además, presente una respuesta rápida.

El controlador de lógica difusa (CLD) obtuvo buenos resultados en la respuesta a escalón (figura 9), de lo cual se concluye que este controlador puede usarse en el arranque de la planta. El controlador difuso en este tipo de situaciones hace que la planta se comporte mejor.

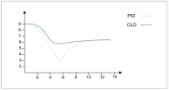
En la prueba a una señal de entrada combinada (escalón-rampa) los resultados con el controlador PID fueron ligeramente mejores, de lo cual se concluye que el PID tiene un mejor seguimiento a la rampa que el controlador difuso, ya que éste presenta un comportamiento lineal.

Una de las pruebas que llamó la atención, fue la de excitar el sistema con una señal escalón inversa. Los resultados que se obtuvieron para el PID fueron al principio desconcertantes, pues se esperaba un buen seguimiento, de lo cual se puede concluir que, debido a la histéresis del sistema, el PID responde de forma diferente. No así, el controlador difuso, el cual se adapta a la no linealidad del mismo.

Conclusiones de lógica fuzzy

Con el propósito de comparar el desempeño del controlador lógico difuso, se diseñó e implantó un controlador convencional PID, tomado de las librerías de Simulink de MATLAB.

El desarrollo del controlador difuso es relativamente sencillo, dado que se cuenta con una metodología definida que per-mite identificar las partes que constituyen la solución del problema de control. Por otra parte, se cuenta con el software adecuado para la estrategia de control difuso (Toolbox Fuzzy de MATLAB).

Posteriormente, al llevar el controlador difuso a la planta, sólo se realizaron pequeños ajustes a los conjuntos difusos de entrada y salida, para adecuarlos a los requerimientos de la misma. No ocurrió así con el controlador PID, el cual se tuvo que ajustar de forma distinta, en la simulación se utilizó el método de límite de estabilidad y en la implantación el método de respuesta transitoria (ambos de Ziegler-Nichols), debido a que la planta presenta un comportamiento no lineal y el PID convencional utilizado es lineal. Los valores de los parámetros del controlador obtenidos con el modelo dan una aproximación a los valores finales utilizados en el controlador real.

Adicionalmente, se puede concluir que es necesario desarrollar trabajos encaminados a optimizar el sistema de control de la variable flujo, que vayan orientados a combinar lo mejor de los controladores difusos y los convencionales, dado que algunas deficiencias de uno pueden ser compensadas con mejores resultados del otro.

Figura 9. Comparativa entre control convencional y fuzzy.

Figura 10. Comparativa combinando rampa y escalón.

Figura 11. Comparativa para respuesta inversa.

Bibliografía

George Bojadziev and Maria Bojadziev. Fuzzy Logic for Business, Finance and Management. 2^nd Edition. Advances in Fuzzy Systems-Aplications and Theory-Vol. 23, World Scientific, New Jersey, 2007.

James J. Buckley, Esfandiar Eslami and Thomas Feuring. Fuzzy Mathematics in economics and Engineering. Physica-Verlag, Heidelberg, New York, 2002.

Arnold Kaufmann y Jaime Gil Aluja. Introducción de la Teoría de los Subconjuntos Borrosos a la Gestión de las Empresas. Milladoiro, Santiago de Compostela, 1986.

Zadeh L. A. (Ed). Fuzzy Sets and Applications: Selected Papers by L. A. Zadeh. John Wiley & Sons, New York, 1975.

Zadeh L. A. Fuzzy sets. Information and Control, 8 (1965), pp. 338-353.