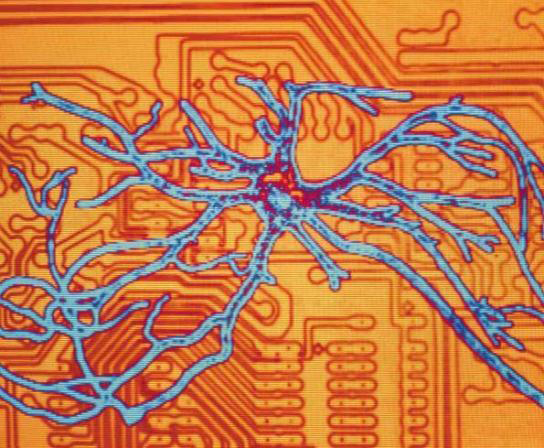
Identificación de sistemas mediante redes neuronales
Las redes neuronales permiten disponer del modelo de un sistema con el que se está trabajando para poderlo regular con precisión y realizar otras funciones
Normalmente son múltiples los procesos que se encuentran en una industria por muy pequeña que sea. Para éstos, es muy interesante en la actualidad poder disponer de un modelo del mismo, que nos puede servir para tareas de diagnosis de fallos, para poder diseñar reguladores que permitan unas especificaciones de funcionamiento muy exactas, etc. En lo referente a la regulación de sistemas, que es algo relativamente reciente, existen diferentes técnicas de identificación. En este documento se aborda una de ellas, y consiste en la identificación de sistemas mediante redes neuronales, que es una de las muchas posibilidades que ofrece el uso de esta técnica.
Este trabajo se desarrolla íntegramente en el ordenador para que pueda ser comprobado por cualquiera, y para ello se escoge un sistema físico del cual se conocen las ecuaciones que describen su funcionamiento. Si se tratase de un sistema real, al cual se le toman los datos para entrenar y validar la red con algún equipo de adquisición de datos, se puede omitir la primera parte, en la cual se generan los datos del sistema. El software utilizado es el Matlab, siendo necesaria la herramienta de redes neuronales. En los sucesivos puntos se detalla la metodología a seguir para aplicar esta técnica.
Sistema a modelizar
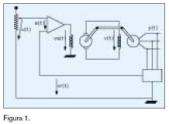
Consiste en la regulación de la tensión a la salida de un alternador. Para tal fin se diseña un circuito de control, que mediante una señal de realimentación vr(t) procedente de la salida y(t) acondicionada, se comparará a su vez con una tensión de referencia de entrada u(t) (consigna), generando un error e(t), que actúa sobre las variables va(t) y v(t) pertenecientes al mecanismo que mueve el alternador y controla su excitación, para regular la salida al valor deseado. El sistema se muestra de forma esquemática en la figura 1.
El sistema viene definido por las siguientes ecuaciones diferenciales:
u(t) – vr(t) = e(t) Ecuación 1
va(t) = 10e(t) Ecuación 2
vr(t) = 0.01y(t) Ecuación 3
200va(t) – 10v(t) = dv(t)/dt Ecuación 4
200v(t) – 25y(t) = dy(t)/dt Ecuación 5
Las ecuaciones 1, 2 y 3 se combinan dando lugar a:
va(t) = 10u(t) – 0.1y(t) Ecuación 6
Implementación del modelo del sistema en Matlab
En este primer apartado del desarrollo se procede a la implementación del modelo de la planta, que va a servir, por un lado, para generar los datos, que serían los que se extraen de uno real, con un equipo adecuado para la adquisición de datos. Y en otro término, va a servir para ver la respuesta de lo que sería el sistema real pudiendo así comparar el resultado de la planta real con el ofrecido por la red neuronal. Conociendo ya las ecuaciones que rigen el funcionamiento del sistema, éstas se introducen adecuadamente en una función de Matlab, a la que se llamará posteriormente desde el resto de subprogramas que se vayan implementando (el nombre de la función es “gmodel”). La función tecleada es la siguiente:
function dy=gmodel(t,y)
% t-tiempo
% y-Estado actual del sistema
% dy-Retorna las derivadas de estado
% Términos del vector de estado
% y(1)- Tensión de salida
% y(2)- Tensión excitación alternador
% y(3)- Entrada al sistema
% ESTADO
ys=y(1);
v=y(2);
u=y(3);
% Cálculo de la tensión de excitación del motor va=10*u-0.1*ys;
% CÁLCULO DE DERIVADAS
dys=200*v-25*ys;
dv=200*va-10*v;
du=zeros(size(u));
% ENTREGA DE DERIVADAS
dy=[dys; dv; du];
Haciendo referencia a la figura 1 en la que se ilustra el sistema, se tiene que el vector de estado está formado por la salida que se pretende controlar (ys), la tensión de excitación del alternador (v) y, por último, la consigna o señal de referencia (u). En un segundo término se tiene el cálculo de la tensión de excitación del motor que mueve al alternador (va). En tercer lugar se teclean las derivadas y, para finalizar, la sentencia que entrega las derivadas resultantes en la función.
Se ha modelado el sistema en su con-junto, entendiendo por éste la inclusión de lo que es la cadena de realimentación con el acondicionamiento de la señal de salida, como paso previo a la comparación con la consigna. Este hecho se lleva a cabo así, ya que de haber realizado tan sólo el del sistema, sale una respuesta muy sencilla, y se pretende aquí realzar la modelización del sistema mediante esta técnica, aunque éste no sea sencillo.
Programa para comprobación de la red neuronal
En este apartado se implementa un pro-grama, mediante el cual se mostrará la respuesta real del sistema (función realizada anteriormente), para contrastarla con la de la red neuronal para unas especificaciones de partida iguales.
% Indicación de las variables de partida
ys=0;
v=0;
u=0.045;
init_state=[ys; v];
% Se obtiene la respuesta del péndulo para 0.15 segundos
[p_time,p_states]=ode23(‘gmodel’,[0 0.15],[init_state; u]);
p_states=p_states’;
plot(p_time,p_states(1,:))
Tras la ejecución de este programa, la respuesta es la de la figura 2.
Si en lugar de pedir que muestre la primera variable se le indica la segunda, el resultado es el mostrado en la figura 3.
Generación de datos para entrenamiento de la red
En este apartado se teclea el código, que me permitirá obtener los datos con los que se entrenará la red neuronal a implementar. Lo que se hace es llevar a cabo múltiples combinaciones de las variables del sistema, haciendo pasar éste por el máximo número de casos posible, dentro de un equilibrio ya que, si no, una cantidad de datos excesiva puede dar problemas en la implementación de la red. El código es el siguiente:
ys=[0:0.5:12];
v=[0:0.15:3];
u=[0:0.01:0.1];
Pm=[combvec(ys,v,u)];
timestep=0.0015;
Q=length(Pm);
Tm=zeros(2,Q);
for i=1:Q
[ode_time,ode_state]=ode23(‘gmodel’,[0 timestep],Pm(:,i));
Tm(:,i)=ode_state(length(ode_state),1: 2)’-Pm(1:2,i); end
La red se ha de entrenar, con datos en todo su rango de funcionamiento, ya que si no se hace así no funcionará bien. En los apartados siguientes se ve que la red no actúa bien en este caso. Los intervalos escogidos para la salida ‘ys’ y para la tensión de excitación del alternador ‘v’, se han escogido, en base a los resultados obtenidos para el intervalo de entrada seleccionado. Tras ejecutar este programa se consiguen dos tablas de datos, ‘Pm de 3×5775’ y ‘Tm de 2×5775’.
Programa para implementación y entrenamiento de la red
En este apartado se muestra el programa realizado para la implementación de la red, así como el entrenamiento de la misma en base a unas premisas. Éstos son datos de partida, pero que han de ser variados para conseguir optimizar el funcionamiento de la red. El código del programa es el siguiente: % Número de neuronas en la capa oculta
S1=8;
% Número de neuronas de la capa de
salida [S2,Q]=size(Tm);
mnet=newff(minmax(Pm),[S1,S2],{‘ta nsig’,’purelin’});
mnet.trainParam.epochs=300;
% número máximo de iteraciones en el entrenamiento
mnet.trainParam.goal=(0.0037^2);
% Mean-squared error goal
% Entrenamiento de la red
mnet=train(mnet,Pm,Tm);
Tras la ejecución de este programa se habrá entrenado la red, cuyas especificaciones se indican en el encabezado del mismo.
Programa para observar los resultados de la red
Se muestra aquí el programa implementado, que permitirá observar los resultados obtenidos, utilizando la red entrenada previamente. El código es el que se muestra a continuación:
% Asignación de datos de partida
ys=0;
v=0;
u=0.045;
timestep=0.0015;
init_state=[ys; v];
time=[0:timestep:0.15];
% Cálculo de las variables
state=init_state;
states=zeros(2,length(time));
states(:,1)=state;
for i=2:length(time)
state=state+sim(mnet,[state; u]);
states(:,i)=state;
end
plot(time,states(1,:),’k’)
hold on
Al final de este programa se indica que se dibuje la variable correspondiente a la de salida (1) y que, además, se ponga la misma en color negro (‘k’), para después generarla con el programa de testeo y poder comparar ambas. Se puede hacer lo mismo con la tensión de excitación del alternador. Si se ejecuta el anterior programa, el resultado es el de la figura 4.
Si ahora se muestra simultáneamente la respuesta con el programa de testeo, el resultado es el de la figura 5.
Comparación de diferentes resultados
Como se puede observar en la figura 5, la aproximación es bastante buena, teniendo en cuenta el orden de magnitud que se está manejando. Se muestra en la figura 6, el resultado para la tensión de excitación del alternador, también comparada con el valor real.
También en este caso la aproximación en muy buena.
Respuesta ante consigna en el límite de entrenamiento
Si ahora se dan como datos de partida la salida ‘ys=0’, la excitación del alternador ‘v=0’ y la entrada ‘u=0.1’ en lugar de 0.45, la gráfica de la salida, para la red y el testeo juntos es el de la figura 7.
En este caso la respuesta es mejor que para valores pequeños, pero para otros entrenamientos con la misma configuración de red, las diferencias son mayores aunque la respuesta siga siendo bastante buena.
Visualización de la respuesta cuando alcanza régimen permanente
Si lo que se hace ahora es poner un tiempo mayor, en el que la señal se estabiliza, el resultado es el que se muestra en la figura 8.
Cuando la señal se encuentra estabilizada tras la sobreoscilación, existe un pequeño error de posición, pero éste es muy pequeño.
Entrenamiento de la red con 12 nodos en la capa oculta
A la red se le modifica ahora el número de nodos en la capa intermedia poniéndole 12 en lugar de 8, y se observan los resultados para un tiempo de hasta ‘0,25’, que son los siguientes en el caso de la salida ‘ys’ (figura 9).
Como se puede observar, a pesar de haber aumentado los nodos en la capa intermedia, los resultados no son tan buenos como en el caso de 8. Para la variable ‘v’ se tiene la figura 10.
Tampoco en este caso se mejoran los resultados.
Entrenamiento de la red con 6 nodos en la capa oculta
Si ahora se ponen 6 nodos, en primer lugar se observa que es necesario realizar más iteraciones para alcanzar la especificación de error en el entrenamiento de la red, y por otro lado, los resultados tampoco son mejores que para el caso de 8 nodos en la capa intermedia, como se muestra en la figura 11.
Entrenamiento de la red con 9 nodos en la capa oculta
Para 9 nodos en la capa intermedia se tiene la figura 12.
Entrenamiento de la red con 9 nodos en la capa oculta
Para 7 nodos en la capa intermedia se tiene la figura 13.
Respuesta ante consigna fuera del límite de entrenamiento
Si ahora se dan como datos de partida la salida ‘ys=0’, la excitación del alternador ‘v=0’ y la entrada ‘u=0.2’, la gráficas de la salida real y la de la red son las de la figura 14.
Lo que ocurre en este caso, es que le estoy dando valores a la entrada de referencia que no se corresponden con los del rango de entrenamiento de la red (están fuera), por ese motivo difiere tanto la señal de testeo de la proporcionada por la red.
Respuesta de la red ante una entrada en rampa
Para este caso es imprescindible la realización de dos nuevos programas, el primero de ellos es para generar la rampa de entrada y ver la salida. Será necesario en cada incremento de tiempo hacer una llamada a la función, en la que se tiene el modelo del sistema, utilizando como entradas los resultados de la iteración anterior, y al mismo tiempo incrementar en un valor fijo el valor de entrada. De este modo se tienen una especie de escalones, pero si se hacen suficientes valores con el resultado se puede asemejar al de una rampa. El listado del código se muestra a continuación:
ys=0;
v=0;
u=0.00045;
init_state=[ys; v];
uu=zeros(101,1);
p_timeall=zeros(101,1);
p_statesall(1,1)=ys;
p_statesall(2,1)=v;
p_statesall(3,1)=u;
uu(1)=0;
t=0;
ti=0.0015;
dti=0.0015;
p_timeall(1)=0;
for i=2:1:101
uu(i)=uu(i-1)+u;
p_timeall(i)=ti;
[p_time,p_states]=ode23(‘gmodel’,[tti],[init_state; uu(i)]);
p_states=p_states’;
ld=length(p_states);% Se coge elúltimo de los valores
t=ti;
ti=ti+dti;
ys=p_states(1,ld);
v=p_states(2,ld);
init_state=[ys; v];
p_statesall(1,i)=p_states(1);
p_statesall(2,i)=p_states(2);
p_statesall(3,i)=p_states(3);
end % Se obtiene la respuesta del péndulo para 0.15 segundos
hold on
plot(p_timeall,p_statesall(1,:))
El segundo de los programas es para visualizar la respuesta ante entrada en rampa en la red neuronal ya entrenada. En este caso, sólo es necesario inicializar la entrada y, después, en el bucle utilizado para simular la red se incrementará en cada iteración dicha entrada. El código es el siguiente:
ys=0;
v=0;
u=0.00045;
timestep=0.0015;
init_state=[ys; v];
time=[0:timestep:0.15];
state=init_state;
states=zeros(2,length(time));
states(:,1)=state;
for i=2:length(time)
state=state+sim(mnet,[state; u]);
states(:,i)=state;
u=u+0.00045;% incremeneto de la entrada en cada iteración
end
plot(time,states(1,:),’k’)
hold on
Salida ante entrada rampa para una red con 8 nodos en la capa oculta
En este caso se entrena la red con 8 nodos en la capa intermedia y, posteriormente, se ejecutan los programas mostrados previamente, para mostrar simultáneamente ambas gráficas. Dicha gráfica se muestra en la figura 15.
En ella se puede observar que la aproximación es bastante buena.
Salida ante entrada rampa para una red con 6 nodos en la capa oculta
Ahora se entrena la red con 6 nodos en la capa intermedia. El resultado es el de la figura 16.
Las diferencias en este caso son mucho mayores que en el anterior.
Salida ante entrada rampa para una red con 10 nodos en la capa oculta
Ahora se entrena la red con 10 nodos en la capa intermedia. El resultado es el de la figura 17.
Ahora la respuesta real de la de la red se aleja, tanto en forma como en magnitud, excesivamente.
Conclusiones
La identificación de sistemas, mediante el empleo de redes neuronales, como se puede comprobar es buena. En ocasiones mejor que empleando otra técnica diferente. No existe una metodología para asegurar la consecución de buenos resultados. Se ha intentado a lo largo de todo el documento, con la realización de un alto número de ejemplos contemplando diferentes casos, que la forma de la red, así como las especificaciones para el entrenamiento en cuanto a iteraciones y tasa de error permitido, van a provocar que la identificación sea buena o no. Esto es una característica de las redes neuronales, pues no existe una regla para saber la configuración adecuada de ante-mano, sino que lo que prima es la experiencia y el “olfato” a la hora de definirla.