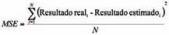Herramientas de redes neuronales para ingeniería de procesos industriales
RESUMEN
El uso de herramientas de inteligencia artificial, como las redes neuronales artificiales (RNA), es cada vez más habitual en distintos ámbitos industriales como pueden ser el control de procesos y de la calidad y la predicción de fallos operacionales. Existen herramientas basadas en RNA capaces de facilitar aspectos de la ingeniería de procesos con un esfuerzo de aprendizaje relativamente pequeño, hasta el punto de que algunas de esas herramientas pueden ser usadas como funciones o plug-in de hojas de cálculo comerciales, sumando su potencia computacional a las funciones de cálculo y análisis que estas últimas ofrecen. La utilización eficaz de un modelo de RNA requiere de una sistemática, para obtener el máximo partido de la información disponible. NNpred y Alyuda Forecaster XL son dos herramientas de software de RNA que sirven de apoyo a la ingeniería de procesos industriales y sobre las cuales se ha realizado un estudio y comparativa de uso, para la predicción de fallos en una planta de tratamiento de aguas residuales urbanas.
Recibido: 2 de febrero de 2010
Aceptado: 16 de marzo de 2010
Palabras clave
Redes neuronales, inteligencia artificial, software, procesos industriales, aguas residuales
ABSTRACT
The use of artificial intelligence tools such as Artificial Neural Networks (ANN), is becoming increasingly common in a wide range of industrial areas such as process control, quality control and failure prediction. There are ANN based tools which are capable of facilitating aspects of process engineering with a relatively minimal learning process, even to the point where certain of these tools can be used as functions or plug-ins for commercial spread sheets, adding their computational power to the calculation and analysis capabilities offered by these spread sheets. The effective utilisation of an ANN model requires classification in order to obtain the full potential from the available information. NNpred and Alyuda Forecaster XL are ANN software tools, which serve to support Industrial Process Engineering, which have been subjected to a study and comparison of use, in failure prediction in an urban waste-water treatment plant.
Received: February 2, 2010
Accepted: March 16, 2010
Keywords
Neural networks, artificial intelligence, software, industrial processes, wastewater
Pese a lo que su nombre parece sugerir, las redes neuronales artificiales (RNA) son un conjunto de técnicas computacionales con una extraordinaria capacidad para ajustar modelos tipo caja negra de un sistema. Su concepción está inspirada en la forma en que las neuronas se conectan e interaccionan entre sí para producir pensamientos y conclusiones. Sin embargo, su diseño y funcionamiento tienen una fuerte base matemática, renunciando a ser una simulación exacta de las corrientes eléctricas y sinapsis de las neuronas biológicas.
El funcionamiento básico de una RNA consiste en entrenarla para que aprenda a asociar unas características del sistema (las salidas deseadas) con otras características del mismo (entradas), a partir de datos del sistema que se quiere modelar. Además, presentan una capacidad de generalización que les permite, por un lado, pronosticar salidas (comportamientos) ante entradas (situaciones) que no han visto nunca antes y, por otro, abstraerse del ruido en las señales. En sistemas estocásticos, en los que el desconocimiento de algunas de las variables relevantes lleva a una incertidumbre inherente, esto es especialmente útil.
Las RNA tipo perceptrón multicapa son las más implementadas con diferencia. En éstas, la utilización consta de dos pasos: a) el entrenamiento de la RNA con datos del sistema y b) la utilización de la misma ante nuevos datos (situaciones) que se le vayan mostrando, con objeto de predecir o clasificar el comportamiento que se podrá esperar en esas nuevas situaciones.
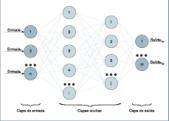
Un perceptrón multicapa consiste en varias capas de neuronas artificiales, cada una de las cuales calcula una salida en función de las entradas que recibe, usando un modelo matemático no lineal. Las salidas de las neuronas de una capa se usan como entradas de las neuronas de la siguiente capa a modo de conexión entre neuronas, multiplicándolas por un factor, el peso de la conexión y así sucesivamente hasta obtener las salidas de las neuronas de la última capa, que son, a su vez, las salidas o resultados de la RNA en su con-junto (figura 1).
El entrenamiento de un perceptrón multicapa parte de una red inicial. Se van mostrando los datos a la red una y otra vez, calculando las salidas que produce. Los pesos de las conexiones se van ajustando de manera que la red vaya produciendo, cada vez con mayor precisión, las salidas deseadas. El ajuste de esos pesos se realiza de manera que se minimice el error cuadrático de las salidas. El resultado de este proceso es un modelo matemático no lineal, capaz de:
– Reproducir con la mayor precisión posible las salidas deseadas en los datos de entrenamiento.
– Generalizar, prediciendo la salida más probable ante nuevas entradas o situaciones del sistema.
– Generalizar, ignorando el ruido o cualquier otra alteración de las salidas que no obedece a una causa descrita en los datos de entrada.
Con todo ello, las RNA son una herramienta matemática extraordinariamente capaz de ajustarse al comportamiento de un sistema, basándose exclusivamente en los datos del mismo.
En este artículo vamos a explicar cómo esta capacidad de modelado matemático ha sido implementada en dos herramientas de software (NNpred y Alyuda Forecaster XL), así como una comparativa de los resultados obtenidos al utilizar dichas herramientas para predecir fallos en una planta de tratamiento de aguas residuales urbanas, como ejemplo aplicativo.
Además, se describen en detalle un conjunto de recomendaciones útiles para sacar el máximo partido de estas herramientas con el fin de utilizarlas en aplicaciones de ingeniería de procesos industriales.
Recomendaciones de uso
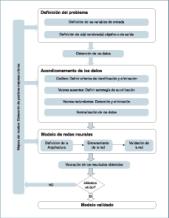
Para la eficaz utilización de herramientas de RNA en ingeniería de procesos, se recomienda seguir una sistemática que permita sacar el máximo partido de los datos disponibles (figura 2).
Esta sistemática consta de cuatro pasos, que se describen a continuación:
1. Definición del problema por modelar.
2. Acondicionamiento previo de los datos.
3. Ajuste del Modelo de RNA.
4. Validación del modelo.
Deficnición del problema
El primer paso es la definición del problema que se pretende resolver mediante la utilización de un modelo basado en RNA. Conceptualmente, se pueden distinguir diferentes problemáticas, como la predicción, la clasificación, la aproximación de funciones y la detección de datos anómalos, entre otros. El tipo de problema que hay que resolver no influye en gran medida en la sistemática que se sigue, puesto que no depende del modelo de redes neuronales que se utilice. El problema quedará definido cuando se identifiquen y definan tanto las variables de entrada, como las variables de salida del sistema en análisis:
– Variables de entrada: son aquellas variables necesarias para definir el sistema y con las cuales se considera que es posible resolver el problema planteado. A la hora de definir estas variables, habrá que tener en cuenta que un número demasiado reducido de ellas podría suponer que el modelo obtenido no tuviese la capacidad de resolver el problema. Por otro lado, una gran cantidad de variables de entrada podría llegar a incluir variables redundantes y reducir sustancialmente la eficiencia computacional del modelo al hacerlo más complejo. Por tanto, a la hora de elegir las variables, será necesario incluir como mínimo aquellas que se considera que influyen de forma clara en la salida y que son suficientes para caracterizarlo inequívocamente.
– Variables de salida: son las variables desconocidas que forman el problema del sistema en estudio, y que se desea predecir o estimar por medio de la RNA a partir de las variables de entrada. Como mínimo, habrá una variable de salida, aunque dependiendo del problema en estudio puede haber varias. En el caso de problemas de predicción, las variables de salida son las que se quieren predecir partiendo de las de entrada. En el caso de problemas de clasificación o diagnóstico, el objetivo del modelo es llegar a realizar una clasificación adecuada del estado del sistema por medio de dichas variables, partiendo de los datos disponibles en las variables de entrada.
Obtención de muestras de datos
Para poder llegar a obtener un modelo útil y que satisfaga unos criterios mínimos de resolución del problema en estudio, será necesaria la obtención de muestras o ejemplos de datos para el entrenamiento de la RNA, y la creación de una base de datos o dataset del problema. La cantidad de muestras necesarias para ello dependerá en gran medida del problema concreto que se tenga entre manos. Es evidente pensar que a mayor número de variables, tanto de entrada como de salida, es necesaria una mayor cantidad de muestras para entrenar eficazmente la RNA. Lo ideal sería poder disponer de la mayor cantidad posible de muestras a la hora de crear el modelo. Pero, en la mayoría de los casos reales, la cantidad de información disponible es limitada, y por tanto, se hace necesario probar el modelo con las muestras de las que se dispone.
Acondicionamiento de los datos
En la mayoría de los casos, antes de poder utilizar los datos obtenidos en las muestras hay que realizar un proceso de acondicionamiento de los mismos. El objetivo es comprobar la validez de estos datos para asegurar que el modelo de redes neuronales se cree con datos de suficiente calidad. Si se llegasen a utilizar datos erróneos, el modelo podría llegar a no ser útil.
Se identifican las siguientes necesidades de acondicionamiento de datos:
Outliers
Los outliers son aquellas muestras excepcionales, que a priori están fuera de los rangos habituales de trabajo y que pueden representar un problema para modelar su comportamiento. Pueden corresponder a errores en su adquisición o también pueden ser causados por estados excepcionales de funcionamiento del sistema que se esté estudiando. Por ello, hay que definir unos criterios de identificación y eliminación de outliers:
– Identificación: se pueden utilizar distintas estrategias de identificación de outliers, dependiendo del problema. En algunos casos, si se tiene suficiente información sobre las variables de entrada, será posible establecer unos límites inferiores y superiores que se sepa que nunca se pueden sobrepasar y que, en caso de ocurrir, se considerarán outliers. En otros casos, no se dispondrá de esta información y habrá que identificar los outliers por otros criterios. Un método muy eficaz es graficar las muestras: aquellas muestras aisladas que se alejan claramente del resto pueden, a menudo, corresponder a outliers.
– Tratamiento: una vez identificados los outliers, hay que decidir qué hacer con ellos. Una estrategia puede ser eliminarlos del dataset. Otra puede ser sustituirlos por otro valor que sí que esté dentro de los límites marcados. A la hora de elegir con qué valor sustituir los outliers, se pueden usar las mismas estrategias que con los valores ausentes, y que se explican a continuación.
Valores ausentes
En el dataset es posible que haya valores ausentes o no disponibles (missing values). En el caso de procesos industriales, por ejemplo, es común que no puedan adquirirse todos los datos de las variables definidas debido a varios motivos, como el fallo de sensores, de comunicación del autómata programable con el ordenador, etcétera. Se puede utilizar alguna de las siguientes estrategias a la hora de decidir qué hacer con estos valores ausentes:
a) Eliminar: se eliminan aquellas muestras en las que falta algún dato, para obtener un dataset completo, en el que no falte ningún dato. Esta estrategia puede ser arriesgada en los casos en los que haya muchos valores ausentes, porque se corre el riesgo de disminuir notablemente la cantidad de datos disponibles.
b) Reemplazar: se reemplazan los datos que faltan por uno de:
– Media.
– Mediana.
– Mínimo.
– Máximo.
– Media de los n valores vecinos.
– Valor por defecto.
Variables redundantes
A la hora de fijar las variables de entrada que definan el problema en estudio, es posible que finalmente se elijan algunas que sean dependientes unas de otras. Si el grado de correlación entre las variables de entrada es alto, se estarán utilizando variables redundantes para definir el modelo. Esta redundancia no aporta información adicional, pero sí que complica el modelo y computacionalmente lo hace menos eficiente. Por tanto, es posible hacer un estudio estadístico del grado de correlación entre las variables de entrada para eliminar las que sean claramente dependientes de otras y simplificar así el modelo.
Normalización de los datos
En función de la herramienta de RNA que se utilice, es posible que se requiera normalizar los datos, de forma que se transformen todas las variables al rango [0,1], o [-1, +1]. La interpretación de los resultados obtenidos requiere en estos casos la desnormalización de los datos resultantes (salidas), volviendo a convertirlos a su rango físico de trabajo.
Ajuste del modelo de redes neuronales:
Una vez realizadas las etapas previas de obtención y acondicionamiento de los datos, es posible utilizarlos para crear un modelo basado en redes neuronales. La creación de este modelo consta de las siguientes etapas:
– Definición de la arquitectura: hay que definir una arquitectura concreta del modelo de RNA que se quiere crear. Se entiende por arquitectura el número de capas y neuronas que forman la red neuronal (figura 1). Algunas herramientas pueden proponer automáticamente una arquitectura, de manera que el usuario no tenga que preocuparse de ello.
– Entrenamiento de la red: consiste en mostrar a la red parte de las muestras acondicionadas anteriormente, para que ésta calcule las salidas producidas y ajuste su comportamiento (los pesos de las conexiones) a las mismas. Para ello, se suele hacer una partición del dataset en datos de entrenamiento y datos de validación. El primero consiste en mostrarle sucesivas veces todas las muestras de entrenamiento, hasta que se considera que las ha aprendido. Se denomina ciclo de entrenamiento o epoch, a cada presentación de todas las muestras de entrenamiento a la red.
– Validación de la red: consiste en mostrarle las muestras no utilizadas en el entrenamiento para valorar su capacidad de generalización según las salidas producidas. La validación suele ser el criterio preferente de detención de los ciclos de entrenamiento.
Validación del modelo
Después de ajustar el modelo de redes neuronales, hay que realizar una valoración de los resultados obtenidos. Si estos resultados se consideran satisfactorios al utilizar el modelo de redes neuronales, quedará validado para poder resolver el problema concreto que se ha considerado. Si, por el contrario, los resultados no cumplen los criterios mínimos exigidos, habrá que mejorar el modelo detectando posibles mejoras o fallos en los pasos anteriores: redefinición del problema, reacondicionamiento de datos, redefinición de la arquitectura, entrenamiento y validación de la red.
Herramientas de RNA bajo prueba
En el mercado actual existen varias herramientas de redes neuronales artificiales. De todas estas herramientas se han seleccionado dos, por considerarlas de fácil uso e integrarse bien en hojas de cálculo Excel, de manera que se facilita en gran medida el trabajo sobre datos ya disponibles en este formato. Ambas pueden ser utilizadas sin tener conocimientos previos sobre redes neuronales, si se siguen las pautas que se indican en este artículo.
NNpred1: es una herramienta gratuita de RNA para hacer predicciones. Su creador es Angshuman Saha, trabajador de GE Global Research, que se encuentra en el Centro Tecnológico John F. Welch, en Bangalore, India. NNpred está desarrollada completamente en Excel e implementa una red neuronal multicapa del tipo FeedForward con retropropagación. No es necesario instalar esta aplicación, puesto que es un archivo Excel en el que directamente se pueden copiar las hojas o los datos de trabajo y crear el modelo. Incluye, además, unas breves instrucciones de cómo usarla para construir un modelo predictivo (figura 3).
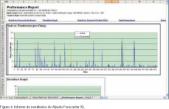
Alyuda Forecaster XL2: se trata de una herramienta comercial de pago de la empresa Alyuda Research Company, pero hay a disposición de los usuarios una versión de demo gratuita. Permite crear y aplicar un modelo de RNA para realizar predicciones, clasificación, aproximación de funciones y detección de datos anómalos (figura 4).
En las tablas 1 y 2 se presenta una comparativa entre las dos herramientas con sus características principales y en la tabla 3, sus limitaciones más destacables.
Pruebas realizadas y resultados obtenidos
El caso de estudio presentado a continuación propone determinar la capacidad de las dos herramientas explicadas anteriormente para predecir el estado de funcionamiento de una planta de tratamiento de aguas residuales urbanas.
Para ello, se ha utilizado un dataset de acceso público disponible en la página web de UCI Machine Learning Repository3. Este dataset proviene de las medidas diarias de sensores en una planta de tratamiento de aguas residuales urbanas. El objetivo es clasificar el estado de funcionamiento de la planta para poder predecir fallos, partiendo de los estados de las variables de la planta en cada una de las etapas del proceso de depuración.
Se ha creado un modelo de RNA en cada una de las herramientas, siguiendo la sistemática propuesta.
Definición del problema que modelar
Este dataset dispone de una muestra de 527 días con sus correspondientes estados de funcionamiento de la planta de depuración. Estos datos están organizados en 38 entradas, según las cuales se quiere poder predecir el funcionamiento que tendrá la planta. Entre estas entradas, hay datos generales de la planta, del primer y segundo decantador y de salida y varios rendimientos. El objetivo es clasificar el estado de funcionamiento de la planta para poder predecir fallos. Se distinguen dos estados de funcionamiento de la planta: el normal y el anómalo. Es decir, hay una única salida categórica que puede tener dos posibles valores, que se ha codificado de forma numérica con un 1 para definir el estado de funcionamiento normal y con un 10 para el estado de funcionamiento anómalo, como se puede ver en la tabla 4. Los valores ausentes se muestran con el símbolo ?
Acondiconamiento previo de los datos
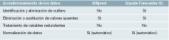
– Identificación y eliminación de outliers: En esta prueba realizada no se han detectado outliers, ya que el objetivo es descubrir fallos en la planta depuradora, posiblemente producidos por datos fuera de lo común.
– Eliminación o reemplazo de valores ausentes: los valores ausentes se han reemplazado por la media de la columna en ambas herramientas.
– Tratamiento de variables redundantes: el dataset estaba ya tratado en este sentido y libre de variables a priori redundantes.
– Normalización de datos: ambas
Ajuste del modelo de RNA
El ajuste del modelo en la prueba realizada se resume en la tabla 5.
Validación del modelo
Ambas herramientas prevén dos tipos de errores que permiten realizar una comparación entre los resultados obtenidos:
a) MSE: error medio cuadrático (del inglés Mean Square Error), que es la media de las diferencias al cuadrado entre el resultado real y el estimado (donde N es el n?mero de muestras de validación).
b) ARE: error relativo absoluto (Absolute Relative Error), expresado en porcentaje, da una medida del error medio de estimación, referente al resultado real.
Resultados obtenidos con NNpred: como se puede comprobar en estos datos (figura 5 y tabla 6), el error en el entrenamiento tiende a cero (ARE = 0,36%), mientras que el error en la validación disminuye notablemente desde ARE = 33,85% en el primer ciclo, hasta el 2,61% al terminar los 2.500 ciclos de entrenamiento. Estos errores se consideraron lo suficientemente pequeños como para dar por válido este modelo.
Una vez entrenada la red neuronal, se utilizaron las 527 muestras totales para comprobar su capacidad predictiva. Los resultados obtenidos fueron los siguientes: de los 527 registros, únicamente se obtuvieron estimaciones erróneas en 2 de ellos. Es decir, el modelo de RNA fue capaz de predecir correctamente todos y cada uno de los estados de funcionamiento normal de la planta depuradora y sólo falló en la estimación de 2 de los estados de funcionamiento anómalos.
Resultados obtenidos con Alyuda Forecaster XL: como se puede comprobar en los resultados (tabla 6), el número de estimaciones erróneas realizadas por esta herramienta es de 7 sobre 527. Mientras que en el dataset de entrenamiento este error supone el 0,95%, en el de validación aumenta hasta el 3,86%.
Conclusiones
Las herramientas de análisis inteligente de datos cada vez están más extendidas y soportan funciones más y más complejas. Un ejemplo son las herramientas de Tabla 7. Tabla de errores medios de entrenamiento y validación en los diferentes ciclos de entrenamiento. redes neuronales artificiales (RNA), como las mostradas en este artículo. Su utilización con fines prácticos no siempre está b) ARE: error relativo absoluto (Abso-entrenamiento tiende a cero (ARE = reñida con la facilidad de uso, y algunas lute Relative Error), expresado en por-0,36%), mientras que el error en la vali-de estas herramientas están perfectacentaje, da una medida del error medio dación disminuye notablemente desde mente integradas en hojas de cálculo de estimación, referente al resultado real. ARE = 33,85% en el primer ciclo, hasta como Excel, lo que facilita su utilización Resultados obtenidos con NNpred: el 2,61% al terminar los 2.500 ciclos y las convierte en una herramienta más como se puede comprobar en estos de entrenamiento. Estos errores se de la hoja de cálculo. En este caso, en una datos (figura 5 y tabla 6), el error en el consideraron lo suficientemente pe-herramienta que permite predecir com-
Utilización del modelo
La utilidad de los modelos así entrenados consiste en que a partir de ese momento, el usuario dispone de una potente herramienta capaz de predecir o clasificar futuros estados. Por ejemplo, ante una nueva situación no observada anteriormente, como la descrita por los datos de la tabla 8.
El modelo es capaz de clasificarla y así predecir si el funcionamiento está siendo normal o anómalo y, de esa manera, tomar a tiempo las medidas oportunas. En este caso, ambos modelos (el de NNpred y el obtenido con Alyuda Forecaster XL) dan como resultado los obtenidos en la tabla 9.
En ambos casos, el valor está más cercano a la categoría de estado normal (valor 1), por lo que puede concluirse que el estado, con más del 98% de probabilidad según el primer modelo y más del 96% según el segundo, será de funcionamiento normal.
Conclusiones
Las herramientas de análisis inteligente de datos cada vez están más extendidas y soportan funciones más y más complejas. Un ejemplo son las herramientas de redes neuronales artificiales (RNA), como las mostradas en este artículo. Su utilización con fines prácticos no siempre está reñida con la facilidad de uso, y algunas de estas herramientas están perfectamente integradas en hojas de cálculo como Excel, lo que facilita su utilización y las convierte en una herramienta más de la hoja de cálculo. En este caso, en una herramienta que permite predecir comportamientos de un proceso, malfuncio-herramientas de pago, las cuales prones o estados de la planta. Estas funcio-porcionan unas funcionalidades muy nes avanzadas están al alcance del mundo completas y un buen acabado. Sin de la ingeniería normalmente a través de embargo, también existen algunas herramientas gratuitas que permiten realizar las mismas funciones con igual o mayor precisión en algunos casos, aunque sea con un acabado menos depurado y con menos funciones de tipo avanzado. Un ejemplo se ha descrito en este artículo, en el que para el caso de ejemplo, y dedicando el mismo tiempo de preparación del modelo, se han obtenido mejores resultados con la herramienta gratuita que con la de pago. Posiblemente, una mayor dedicación de tiempo a depurar el modelo habría conducido a resultados muy similares en ambas. Sin embargo, un factor relevante es el poder llegar a resultados con el menor tiempo de preparación y con la mayor facilidad de uso posible, y eso es lo que se ha procurado demostrar.
Bibliografía
http://www.geocitrus.com/adotsaha/index.html
http://www.alyuda.com/neural-networks-software.htm
Asuncion A, Newman DJ. (2007). UCI Machine Learning Repository [http://www.ics.uci.edu/ ~mlearn/MLRepository.html]. Irvine, CA: University of California, School of Information and Computer Science.