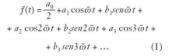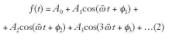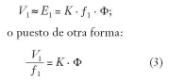Estrategias y circuitos de control de la velocidad de los motores de inducción

Análisis de las técnicas, estrategias y circuitos de control de la velocidad de los motores de inducción, ampliamente utilizados en aplicaciones industriales

Circuito de control

El circuito de control, o carta de control, es el cuarto componente principal del convertidor de frecuencia y tiene cuatro tareas principales:

– Controlar los impulsos o señales que hacen entrar en conducción a los semiconductores del convertidor.

– Intercambio de datos entre el convertidor de frecuencia y los periféricos.

– Recoger y presentar los mensajes de falta.

– Llevar a cabo las funciones de protección para el convertidor de frecuencia y el motor.

Los elementos básicos de que consta el circuito de control, son los siguientes:

Microprocesador: el núcleo de la parte de control es el microprocesador, el cual ha incrementado la velocidad del circuito de control, aumenta significativamente el número de aplicaciones adecuadas para los accionamientos y reduce el número de cálculos necesarios. En el microprocesador se almacena el pro-grama de funcionamiento del equipo y los valores de los parámetros que definen el servicio a realizar en cada caso. El sistema calcula los impulsos de excitación necesarios para obtener la salida de tensión modulada senoidalmente, procesa los datos y señales de entrada y emite las señales de salida necesarias para poder conocer externamente el funcionamiento del equipo. El tipo y cantidad de señales a que se puede acceder desde el exterior, depende del tipo de equipo y de su complejidad.

El microprocesador está integrado en el convertidor de frecuencia, y permite determinar la óptima característica de pulsos para cada estado de funcionamiento.

Convertidor analógico-digital/digitalanalógico: todas la señales que llegan al microprocesador, tanto desde el exterior como desde el interior del equipo, es preciso que sean adaptadas previa-mente. Para realizar esta operación, el circuito de control necesita disponer de un convertidor analógico-digital y otro digital-analógico. Cuando las señales son analógicas y van hacia el microprocesador, es preciso convertirlas previa-mente en señales digitales, operación que realiza el convertidor analógicodigital. Cuando las señales que proceden del microprocesador, el cual sólo proporciona señales digitales, han de transmitirse al exterior, es preciso que, previamente, se conviertan en analógicas, operación que realiza el convertidor digital-analógico.

Para realizar la puesta en servicio es preciso un sistema que comunique el equipo con la persona encargada de realizar esta operación. Para ello, los convertidores suelen llevar un indicador en el que aparecen los diversos valores a fijar para el servicio, así como los posibles fallos y estados de funcionamiento del equipo.

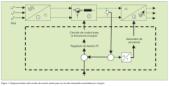
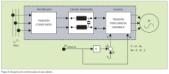
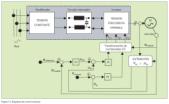
Circuito de control para un convertidor de frecuencia PAM

La figura 1. muestra un convertidor de frecuencia PAM controlado con un circuito intermedio chopper. Los circuitos de control del chopper (2) y el inversor (3).

Esto se hace de acuerdo con el valor momentáneo de la tensión del circuito intermedio.

El circuito intermedio de tensión controla un circuito que funciona como un contador de direcciones en la memoria de datos. La memoria tiene las secuencias de salida para la característica de pulsos del inversor. Cuando la tensión del circuito intermedio aumenta, el contador va más rápido, la secuencia se completa antes y la frecuencia de salida aumenta.

Con respecto al control chopper, la tensión del circuito intermedio se compara primero con el valor de la señal de referencia, que es una señal de tensión. Se espera que esta señal de tensión proporcione unos valores correctos de tensión y frecuencia de salida. Si las señales de referencia y del circuito intermedio varían, un regulador PI informa a un circuito que el ciclo de tiempo debe ser modificado. Esto conduce a un ajuste de la tensión del circuito intermedio a la señal de referencia.

PAM es la tecnología tradicional para el control de los inversores de frecuencia. La técnica de modulación de anchura de impulsos (PWM), es más moderna y se explica a continuación.

Técnica de modulación de anchura de impulsos (PWM)

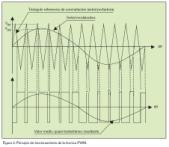
Esta técnica fue propuesta por primera vez por Schömung y Stemmler. El método básico consiste en generar una onda senoidal (tres desfasadas 120º en sistemas trifásicos), de bajo contenido armónico, de la misma frecuencia que la onda de salida del inversor, y con una amplitud proporcional a la requerida y compararla con una onda de tensión triangular simétrica de frecuencia elevada. Los puntos de intersección de la onda senoidal (moduladora) con la triangular (portadora), determinan los instantes de conmutación de los semiconductores y, en consecuencia, la anchura de los sucesivos bloques de tensión continua aplicada a la salida. Así pues, la modulación se basa en la modificación de la anchura de los pulsos, en función del valor eficaz de la onda de salida requerida. Variando la relación V_tM/V_sM se controla el valor de la tensión eficaz de salida. La frecuencia, viene controlada por el período de repetición de la onda configurada. En algunos inversores la frecuencia de la portadora es fija, en otros varía continuamente o se modifica en función de la modulación, y en algunos casos el usuario puede seleccionarla de acuerdo con sus necesidades y las posibles resonancias mecánicas.

En un principio, la generación de la senoide (moduladora) y de la triangular (portadora), se realizaba con técnicas analógicas. Actualmente se realizan de forma híbrida, grabando los valores de la senoide en una memoria que se lee a la frecuencia deseada, y después de ser convertida a una señal analógica, mediante un convertidor analógico-digital, se compara con la triangular de alta frecuencia. Este método es aceptado en gran medida gracias a la aparición de los microprocesadores que, conjuntamente con el soporte de circuitos integrados VLSI, permiten realizar el control PWM.

La utilización de una onda senoidal como señal moduladora no es la única opción, también se suelen emplear ondas trapezoidales.

Modulaciones digitales con moduladora escalonada

También se obtiene una buena precisión si se compara la onda triangular con una onda escalonada, que tenga por semiperíodo los mismos escalones N que el número de impulsos deseados. La altura de cada escalón ha de ser igual al valor de una senoide, en el punto medio de ese escalón.

Modulación con supresión controlada de armónicos

Las formas de onda no senoidales, se pueden analizar aplicando un desarrollo en series de Fourier. Cuando la onda es periódica y acotada, se puede descomponer en la suma de una componente continua, A₀, una componente fundamental senoidal de la misma frecuencia y una serie de armónicos, también senoidales, cuya frecuencia es el doble, triple, etc., de la que tiene la onda de partida.

Así pues, supongamos que f(t) es una función periódica de período T, su frecuencia fundamental es f = 1/T, y la pulsación fundamental es ? ^–=2· p · ƒ. Según Fourier la función se puede descomponer en una suma de funciones seno y coseno con frecuencias múltiplos enteros de la fundamental:

Agrupando los términos seno y coseno de igual frecuencia, puede expresarse también como:

Si existe simetría de semionda desaparece la componente continua y todos los armónicos pares. Si en las tres salidas del sistema trifásico, se generan las mismas formas de onda, desfasadas 120º, desaparecen todos los armónicos múltiplos de tres.

Si todo esto se refiere a un motor de corriente alterna, algunos armónicos contribuirán a que el motor gire en sentido correcto, otros crearán un campo de sentido contrario, y la mayoría simplemente lo calentarán. Debido a la reactancia del motor, los armónicos de frecuencia muy elevada tienen poca influencia en la intensidad, y es suficiente con eliminar las frecuencias más bajas.

En general, se puede decir que cuanto más alta sea la frecuencia de la onda triangular, menor será el contenido de armónicos de la senoide de potencia sintetizada. El método de conmutación controlada permite, con muy pocas conmutaciones (por lo que desde este punto de vista el dispositivo de potencia no tiene que ser de frecuencias altas), eliminar los armónicos más perjudiciales para el motor. Normalmente, una onda portadora del orden de kHz pudiera ser suficiente; no obstante, hay que tener en cuenta los posibles problemas ocasionados por las vibraciones que puede producir el motor, las bobinas y los propios conductores. Otro de los posibles problemas es el ruido, ya que el oído humano es muy sensible a sonidos de frecuencia alrededor de 2 o 3 kHz; por otra parte, las frecuencias de 16 kHz o superiores son prácticamente inaudibles, pero entre otros problemas, es posible que ocasionen demasiadas pérdidas en conmutación. Con todo ello, los inversores PWM precisan de semiconductores rápidos, siendo los transistores en sus diferentes versiones, los IGBTs, IGCTs, etc., los semiconductores más apropiados.

En aplicaciones de gran potencia, generalmente el límite lo ponen las altas corrientes y elevadas tensiones de los semiconductores a utilizar, ya que en general, si el semiconductor es muy potente no suele ser tan rápido.

Para implementar en la práctica una modulación con conmutación controlada se recurre, normalmente, a realizar el cálculo de los ángulos de conmutación en un ordenador externo al sistema de control. Una vez realizado esto para las diferentes velocidades, y seleccionando para cada una de ellas qué armónicos se eliminan, se graban en una memoria los ángulos de conmutación obtenidos.

El algoritmo de control se usa para calcular la conmutación del inversor PWM, y se pueden seguir diferentes estrategias.

Estrategias de control

En un accionamiento de velocidad variable, el control de la transferencia de energía se concreta en dos variables mecánicas: par y velocidad. En la práctica, sólo se controla una de estas dos variables, mientras que la otra viene determinada por la carga. Así, si se efectúa un control de par, la velocidad queda determinada por la carga y, viceversa, si se efectúa un control de velocidad, es el par el que viene determinado por la carga.

El motor de corriente continua, gracias a sus favorables características, las cuales se resumen a continuación, es uno de los que mejor cumple las exigencias de un control de velocidad y par, simple y preciso:

– Fácil regulación de velocidad variando la tensión aplicada a los bornes del motor (E=U_i – R_iI_i=C₁.F.n) y/o variando el flujo.

– Par proporcional a la corriente del inducido y al flujo (M_i=C₂.I_i.F), por lo que se puede controlar actuando sobre I_i y/o sobre Ie (corriente de excitación).

– Posibilidad de funcionar como generador, lo cual se puede utilizar, de manera relativamente simple, para el frenado del motor.

No obstante, el motor de corriente continua tiene también sus inconvenientes:

– Su fabricación resulta costosa.

– Necesidad de colector (conmutador), para conmutar de una espira del inducido a otra, siendo este un elemento delicado y que precisa de un mantenimiento continuo.

– Precisa disponer de transductores de velocidad. Por otro lado, el motor trifásico asíncrono (de inducción) presenta las siguientes características, que el motor de corriente continua no tiene:

– Elevada robustez.

– Gran simplicidad.

– Puede trabajar fácilmente en régimen de recuperación de energía en el frenado. No obstante, el motor asíncrono presenta también sus inconvenientes:

– La relativa debilidad de par en el arranque, si se compara con el motor, serie de corriente continua.

– La falta de flexibilidad del motor, donde el régimen óptimo de funcionamiento sólo se sitúa cerca del sincronismo.

– La dificultad de alcanzar un retardo, puesto que no resulta fácil forzar la velocidad.

– En aplicaciones de tracción, no se puede realizar fácilmente la doble tracción.

Con todo ello, y teniendo en cuenta que el comportamiento dinámico del motor asíncrono, queda definido por un sistema de ecuaciones no lineales de orden elevado, se puede concluir que el control de los motores asíncronos resulta mucho más complejo que el de los motores de corriente continua.

Si se considera que el motor asíncrono se encuentra trabajando de forma estable en un punto determinado de su característica de par, manteniendo el flujo constante, entonces se pueden eliminar de las ecuaciones de definición los términos derivada, y bajo estos supuestos su comportamiento queda representado por las ecuaciones lineales que definen el régimen permanente, resultando un análisis del control mucho más simple. Sin embargo, este tipo de controles, denominados escalares, al no tener en cuenta el transitorio, resultan mucho menos precisos.

En las últimas décadas, utilizando nuevos dispositivos y técnicas de control, se ha tratado de conseguir que los motores asíncronos tuviesen el mismo comportamiento dinámico, y nivel de precisión en el control que el de los motores de c.c.; así han surgido los métodos de control vectorial, que tienen en cuenta la fase y utilizan un modelo complejo del motor que tiene en cuenta la orientación del campo magnético, lo cual permite actuar mejor sobre el par durante los transitorios, y obtener así unas mejores prestaciones dinámicas. En algunos casos es preciso conocer la posición del rotor. Entre las técnicas más recientes se encuentra el control directo del par (Direct torque control, DTC) que incluye el inversor dentro del modelo y per-mite conseguir respuestas mucho más rápidas.

Control escalar

El control escalar, denominado también control tensión/frecuencia (V/f), o control del vector tensión (Voltaje Vector Control, VVC), se utiliza como algoritmo de control de los convertidores de frecuencia, en fuente de tensión y se basa en lo siguiente:

Una de las maneras para reducir la velocidad de los motores de c.a. es reducir la frecuencia de alimentación; sin embargo, al reducir la frecuencia por un lado disminuye el par y por otro disminuyen las reactancias (X_L = j? ^–L); por lo que, si se mantiene constante la tensión, podría resultar demasiado elevada la corriente y se podría llegar a quemar el motor. Una forma de evitar este problema, es reducir la tensión en la misma proporción en que lo hace la frecuencia.

Así pues, en definitiva, se trata de controlar la amplitud y frecuencia del vector tensión, usando la compensación de carga y deslizamiento. El ángulo correspondiente al vector tensión, se determina en función de la frecuencia programada para el motor (referencia), y la frecuencia de conmutación de los semiconductores.

Las características del control escalar, son las siguientes:

– Rango de regulación de velocidad: 1:25 sin realimentación.

– Precisión: ± 1% de la velocidad nominal sin realimentación.

– Robusto frente a los cambios en la carga.

– Valor nominal de la tensión a la frecuencia nominal del motor.

En las primeras aplicaciones de esta técnica sólo se lograba un margen de variación de velocidad muy reducido, y ello era debido a que al mantener constante la relación V/f, no se tenía en cuenta que los devanados tenían también resistencia óhmica, la cual era independiente de la frecuencia. Una posible solución a frecuencias bajas, es aumentar un poco más la tensión, o mejor hacerlo en proporción al consumo y la resistencia de los devanados. Muchos inversores permiten seleccionar la relación tensión/frecuencia en función de la carga mecánica.

Si en el estator del motor se desprecia la caída de tensión frente a la f.e.m. inducida, se tiene:

Como puede verse, el flujo en el entrehierro depende de la relación V/f, lo cual indica que se puede variar la velocidad de dos formas:

– Variación a flujo constante.

– Variación por reducción de flujo.

Variación de velocidad a flujo constante

La variación de velocidad a flujo constante, o también llamada a par constante, se basa en que de acuerdo con la expresión: V₁/ƒ₁= K · F si se varía la tensión y la frecuencia, de forma que su cociente se mantenga constante, la onda giratoria de flujo continúa constante.

La tensión solamente puede variar desde cero a su valor nominal, mientras que la frecuencia podrá hacerlo desde cero a valores superiores al valor nominal. Esto limita las posibilidades de mantener el flujo constante.

El control escalar puede realizarse de dos formas:

– En lazo abierto.

– En lazo cerrado.

Control escalar en lazo abierto

Este método controla la velocidad del motor, variando la frecuencia de alimentación de las tensiones del estator.

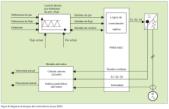
Para velocidades superiores, aproximadamente al 10 % de la velocidad nominal, es correcta la aproximación de que el flujo en la máquina depende únicamente del cociente V/f. Por lo que, si se desea mantener el flujo nominal de la máquina (lo que supone trabajar a par nominal) en todo el rango de frecuencias, se debe mantener constante y en su valor nominal el cociente V/f. Sin embargo, a bajas velocidades esta aproximación pierde progresivamente su validez, al cobrar importancia la caída de tensión en la resistencia del estator; por lo que, de mantenerse la misma ley de control para el cociente V/f, se originaría una progresiva disminución del flujo en la máquina y, por lo tanto, de la capacidad de producción de par. Para evitar esto, generalmente se le suma un valor constante a la tensión calculada a partir de la velocidad (figura 5).

El control escalar en lazo abierto, si bien resulta ser un método de control sencillo y económico, sus prestaciones son reducidas. Este método sólo es adecuado para aquellas aplicaciones industriales que toleran pequeñas variaciones de velocidad, o de flujo en el entrehierro (ocasionadas por variaciones de carga o de tensión), y que no precisan de una respuesta rápida.

Control escalar en lazo cerrado

Para evitar las variaciones no deseadas de velocidad y de flujo, se puede realizar un control escalar en lazo cerrado de estos parámetros. Se dispondrá al menos de dos lazos de control: uno de velocidad que impondrá la frecuencia de alimentación, y otro de flujo que impondrá la tensión. Además, con la finalidad de obtener un sistema más estable, generalmente se introduce un tercer lazo de control para controlar el par. Tanto el par como el flujo pueden ser estimados a partir de las ecuaciones de régimen permanente (figura 6) o bien se pueden medir.

Variación de tensión y frecuencia siguiendo una ley cuadrática

Las bombas centrífugas y los ventiladores presentan un par que varía con el cuadrado de la velocidad; por lo que, si se desea regular la velocidad de los motores de accionamiento de estos dispositivos, será preciso que la ley de variación de tensión y frecuencia del convertidor se ajuste a las características indicadas, para que el par motor se adapte al par exigido por la bomba o el ventilador.

Variación de velocidad por reducción de flujo

Este método de variación de velocidad, se llama también por debilitamiento de campo o a potencia constante.

Cuando se hace variar la frecuencia por encima del valor en que se alcanza la tensión nominal de la red, y teniendo en cuenta que a partir de ese punto la tensión ya no puede seguir creciendo, lo que ocurrirá es que, en esa zona el flujo en el entrehierro, decrecerá paulatinamente con el incremento de frecuencia. En esta situación, el par máximo de la curva par-velocidad, decrecerá en función de la frecuencia, como se puede ver en la figura 7, pudiendo funcionar en esta zona en un régimen de potencia constante, como así se ha señalado por las líneas discontinuas de la citada figura 7. Para un funcionamiento seguro del motor, en la zona de debilitamiento de campo, el par máximo nunca ha de ser inferior a 1,3 veces el par resistivo aplicado.

Control directo de par

Un desarrollo reciente del control escalar es el denominado control directo de par (Direct Torque Control, DTC), bajo el cual se controla directamente la amplitud y el ángulo del vector tensión, así como la frecuencia, y cuyas características superan a las del control escalar normal (VVC):

– Rango de control de velocidad: 1:100 sin realimentación.

– Precisión: ± 0,5 % de la velocidad nominal sin realimentación.

– Mejora de magnetización del motor.

– Amortiguamiento de la resonancia activa.

– Control directo de par (lazo abierto).

– Operación al límite de corriente.

La principal diferencia del control directo de par, con relación a otros métodos de control de los accionamientos de alterna, es que en el DTC no existe un modulador PWM separado, sino que el ángulo de disparo de los semiconductores del convertidor, se determina directamente por el estado electromagnético del motor. Para ello es preciso disponer de un modelo matemático muy preciso del motor, así como una elevada capacidad de cálculo. El nivel de la sofisticación matemática del modelo permite calcular el valor exacto de las variables del mismo, sin necesidad de una realimentación de la velocidad del eje. En la puesta en marcha del sistema, una rutina de identificación proporciona al modelo los valores de la resistencia del estator, la inductancia mutua, los coeficientes de saturación y la inercia del motor. Una parte del modelo modeliza el comportamiento térmico del motor, de forma que corrige las variaciones que ocasione la temperatura en la resistencia del estator.

En funcionamiento normal, el modelo recibe información de las medidas de las corrientes de fase y de la tensión del circuito intermedio de continua, junto con la posición de los semiconductores de potencia (tiristores, transistores, IGBTs, IGCTs, etc.). A partir de estos datos se calculan los valores actuales de las variables de control, que son el flujo magnetizante y el par motor. Asimismo, se calcula la velocidad del eje y la frecuencia eléctrica, con lo que no se precisa disponer de transductores para realimentar en velocidad, en el 95 % de las aplicaciones industriales.

El bloque de control por histéresis del par y del flujo, compara los valores reales de estas variables con sus valores actuales, y determina la posición óptima de los semiconductores del convertidor de potencia, para seleccionar el vector de tensión más indicado. El objetivo es obligar al vector de flujo del estator a evolucionar, de forma que se consigan los valores de referencia de par y de flujo del estator.

Para determinar la secuencia de conmutación del inversor, el DTC utiliza un procesador digital de señal junto con un circuito ASIC. Todas las señales de control se transmiten por fibra óptica para conseguir elevadas velocidades de transmisión. Esta configuración permite ejecutar el algoritmo de control rápidamente (cada 25 microsegundos para un procesador de 40 MHz), de forma que si la carga demanda del motor más par, en la próxima secuencia de conmutación se puede satisfacer esta demanda inmediata y directamente.

El DTC incorpora algunas funciones especiales tales como arrancar el motor en cualquier estado electromagnético, incluso si el motor está girando. El frenado por flujo es parecido al frenado por inyección de c.c., pero durante el frenado por flujo el inversor funciona de forma controlada, con lo que se mejora la capacidad de frenado. El modelo del motor puede calcular automáticamente el nivel óptimo de flujo magnetizante, en función del nivel de carga, de esta manera las pérdidas se pueden reducir en más de un 60 % cuando el motor está en vacío. Cuando existe un microcorte en el suministro de energía eléctrica, el DTC mantiene el nivel de tensión en el circuito intermedio de c.c., de esta forma cuando se recupera el suministro el motor puede seguir funcionando inmediatamente.

Control vectorial

Los accionamientos de velocidad variable de control vectorial han existido desde hace bastantes años; no obstante, es en la última década cuando se utilizan ampliamente en gran número de aplicaciones industriales, ello fue debido a que se requería de una electrónica compleja y costosa para controlar con precisión las corrientes del motor, situación que cambió con la aparición de los potentes y rápidos procesadores de señal DSPs (Digital Signal Processors), los inversores reguladores de corriente con modulación de ancho de pulso (Current-Regulated PWM Inverters) y la aparición de los transistores bipolares de puerta aislada IGBTs (Insulate Gate Bipolar Transistors). Esta evolución tecnológica encadenada ha permitido establecer un hito histórico en la regulación de velocidad de motores de corriente alterna, permitiendo que un motor de corriente alterna suministre el par nominal de cero a la velocidad de régimen, para luego pasar a trabajar a potencia constante y alcanzar velocidades varias veces superiores a la nominal, con capacidad de poder acelerar y desacelerar en ambos sentidos de giro, con un control preciso de la velocidad, el par y la posición en motores de potencia y en servomotores.

Así pues, el control vectorial se utiliza con buenos resultados en diferentes aplicaciones industriales: textiles, bobinadoras, servoaccionamientos, robótica, etc.

La estrategia del control vectorial, se basa en extrapolar la técnica de control de los motores de corriente continua de excitación independiente al ámbito de los motores asíncronos. Para ello y debido a que una máquina de corriente alterna carece de dos devanados desacoplados, uno de excitación (campo) y otro de inducido como tiene la máquina de c.c. de excitación independiente, se recurre a referir el sistema trifásico alterno de corrientes estatóricas a un sistema de coordenadas que gira en sincronismo con el campo giratorio. En este nuevo sistema de referencia las corrientes estatóricas pueden ser tratadas como vectores giratorios, de aquí el nombre de control vectorial o también denominado control de campo orientado. A continuación, lo que se hace es descomponer este vector en dos componentes: una en fase con el campo rotórico y la otra en cuadratura. La primera resulta ser la responsable del flujo magnético de la máquina, y se denomina corriente de magnetización, la segunda es la encargada de generar el par motor, y se la llama corriente activa. Mediante esta transformación de coordenadas se consigue desacoplar el modelo matemático del motor asíncrono, y controlar estas dos componentes independientemente, de forma análoga a como se controlan las corrientes de excitación (campo) y de inducido de una máquina de corriente continua. De esta forma se pueden lograr respuestas dinámicas similares. Una vez que se determinan, en este sistema de referencia giratorio, los valores de ambas componentes, magnetización y activa, se aplica una transformación de coordenadas inversa para obtener las consignas (set-points) de magnitud y fase de las corrientes estatóricas, las cuales se aplican a la entrada del regulador de corriente, que generará como respuesta las señales PWM de disparo de los IGBTs de la etapa de potencia, los cuales generan las tensiones que alimentan los devanados de motor.

Para poder ejecutar las rutinas de transformación de coordenadas, se precisa utilizar el ángulo desarrollado por el rotor, esta necesidad da origen a dos estrategias diferentes:

– Registrar el ángulo del rotor a cada instante mediante un encoder o tacogenerador (Control vectorial de lazo cerrado).

– Estimar el ángulo mediante un observador, lo cual da lugar al denominado control vectorial sin sensor o de lazo abierto (Sensor Less Vector Control).

Mediante la técnica de lazo cerrado, resulta posible ejecutar distintas estrategias de control en función de la variable que se desea regular, así se tiene un control en lazo cerrado de velocidad o de par.

El decidir en qué aplicaciones se precisa realizar un control en lazo cerrado, utilizando un sensor de velocidad, y en cuáles no siempre resulta una tarea fácil. Por regla general, se puede decir que resulta conveniente utilizar sensor de velocidad y control en lazo cerrado, en los siguientes casos:

– En aquellas aplicaciones en que se requiera una elevada precisión en el ajuste de velocidad, típicamente superior al 0,001 % (maquinaría de alta precisión).

– En aquellos casos en que se precise un elevado comportamiento dinámico incluso a bajas velocidades, del orden de los 20 ms (trenes de laminación).

– Necesidad de disponer de un par motor elevado a velocidades inferiores al 10 % de la velocidad nominal, incluso a velocidad cero (grúas con funciones de posicionamiento).

– Aplicaciones que requieran un control de par en un rango mayor a 1:10 (bobinadora, control de tensión de lazo cerrado).

Así pues, el control vectorial se puede diseñar de varias maneras. La mayor diferencia entre ellas es el criterio que se utiliza para calcular los valores de corriente activa, corriente de magnetización (flujo) y par.

Comparando lo que ocurre en un motor de c.c. con un motor asíncrono trifásico, se puede comprender mejor los problemas que se plantean (figura 9). En un motor de c.c., los valores que resultan importantes para generar par –flujo (F) y corriente del inducido (Ii)- son fijos en cuanto a valor y posición de fase, en función de la orientación del devanado de campo y la posición de las escobillas. Además, la corriente de inducido de un motor de c.c. y la corriente que genera flujo (corriente de excitación), forman un ángulo recto.

En un motor asíncrono, la posición del flujo (F) y de la corriente del rotor I_L depende de la carga. Además, a diferencia de un motor de c.c., los ángulos de fase y corriente no se pueden medir directamente a partir del valor del estator.

No obstante, usando un modelo matemático, el par se puede calcular a partir de las relaciones entre el flujo y la corriente del estator. Esta técnica se basa en pasar del sistema trifásico de las corrientes del estator, a un sistema bifásico de ejes d y q solidarios con el vector de flujo en el entrehierro (figura 10). Se puede demostrar que solamente la componente I_sd de la corriente del estator es la responsable del flujo, mientras que la componente I_sq puede ser también ella sola la responsable de la producción de par. Sin embargo, como los cálculos, los cuales usan el modelo dinámico del motor, son complicados, este método sólo es económicamente viable en accionamientos digitales.

Como esta técnica permite realizar el control de la carga independientemente del estado de excitación, es posible controlar dinámicamente los niveles de par del motor asíncrono, del mismo modo que en los motores de c.c., teniendo en cuenta además que se tiene una señal de realimentación. Así se puede indicar que este método de control, aplicable tanto a las máquinas asíncronas como a las síncronas, ofrece las siguientes ventajas:

– Buena reacción a las variaciones de la carga.

– Regulación precisa de velocidad.

– Posibilidad de tener el par máximo en el arranque.

– Comportamiento comparable a los accionamientos de corriente continua.

Básicamente existen dos métodos de control vectorial:

Método directo

Desarrollado por Blaschke y que realiza una medición directa del flujo. Este método no se puede realizar a bajas velocidades, ya que el ruido producido por los armónicos impide una buena lectura del flujo.

Método indirecto

Desarrollado por Hasse y donde se realiza una estimación del flujo a partir de las corrientes del estator y del deslizamiento (figura 11). Este método no presenta el problema del ruido, pero tiene el inconveniente de ser fuertemente dependiente de los parámetros de la máquina y, por lo tanto, sensible a las variaciones de los mismos.

Recientemente se ha sugerido un control vectorial universal, donde el control indirecto opera en el rango de bajas velocidades, pasando a control directo en las altas.

La aplicación a las máquinas de c.a. de las modernas técnicas de control adaptativo, ha sido propiciada por la aparición de microprocesadores con elevada potencia de cálculo y extraordinariamente rápidos, tales como los DSPs que superan sin dificultad los problemas de derivas y de ajuste de “set-point” tan frecuentes en las antiguas versiones analógicas de accionamientos vectoriales, y por la aplicación de las técnicas de control vectorial, que permiten utilizar un modelo de máquina definido por un sistema de ecuaciones de orden no muy elevado. Para poder realizar un buen control, se precisa conocer en detalle las características internas de la máquina a controlar. El problema de una máquina eléctrica es que sus parámetros característicos tales como resistencias e inductancias, varían debido al calentamiento y a la saturación, respectivamente, a lo largo del funcionamiento. La técnica consiste en determinar el valor de los parámetros de la máquina en tiempo real, para calcular en cada instante, teniendo en cuenta la variación de dichos parámetros, el control óptimo.

Características del control escalar (V/f) y del control vectorial del flujo

En los últimos años el control de los motores trifásicos de c.a., se ha desarrollado sobre las bases de dos principios de control diferente:

– Control escalar o control V/f normal.

– Control vectorial del flujo.

Ambos métodos tienen ventajas que dependen, básicamente, de los requerimientos dinámicos del accionamiento y de la precisión.

El control de la característica V/f tiene un rango de regulación de velocidad limitado aproximadamente a 1:20 y a baja velocidad, por lo que se requiere una estrategia de control (compensación) alternativa. Usando esta técnica resulta relativamente simple adaptar el convertidor de frecuencia al motor, siendo además una técnica robusta contra cargas instantáneas en todo el rango de velocidad.

En los accionamientos que utilizan el control vectorial de flujo, el convertidor se debe configurar de forma precisa al motor, lo cual requiere un conocimiento detallado de ambos. También se precisa disponer de componentes adicionales para la señal de realimentación. Algunas ventajas de este tipo de control, son las siguientes:

– Una rápida reacción a los cambios de velocidad y en un amplio rango de velocidades. /

– Mejor reacción dinámica a los cambios de dirección.

– Proporciona una estrategia de control simple para todo el rango de velocidades.

Para el usuario, la solución óptima se encuentra en aquellas técnicas que combinan las mejores propiedades de am-bas estrategias. Se precisa disponer de soluciones donde estén presentes, tanto características como la robustez frente al paso carga/descarga en todo el rango de velocidades –un punto fuerte del control V/f, como una rápida reacción a cam-bios en la velocidad de referencia (como la que se tiene en el control de campo orientado).

Optimización automática de energía

El ahorro de energía es un tema de vigente actualidad, que debe preocupar a todos los ciudadanos, por estar directamente relacionado con el medio ambiente, y que obliga a los gobiernos a adoptar políticas energéticas acordes con los nuevos tiempos.

Por ello en muchas aplicaciones industriales, donde los accionamientos trabajan a diferentes ciclos de carga, se puede ahorrar energía durante el funcionamiento a cargas bajas, reduciendo el flujo magnético.

En muchos accionamientos, particularmente aquellos cuya característica de par resistente es cuadrática (tales como ventiladores y bombas centrífugas), se pueden programar características V/f especiales para incrementar el ahorro de energía.

Existen procedimientos que optimizan automáticamente el consumo de energía para una carga dada, y adaptan la referencia de velocidad que proporciona el valor del flujo magnético para la carga actual, como un compromiso entre el ahorro óptimo, y los requerimientos reales de la aplicación en cuanto a mínimo par.

Los ajustes se basan únicamente en los datos disponibles en el sistema de control; para estas funciones no se necesita un ajuste extra de los parámetros. De forma contraria a la operación de control de velocidad normal, con un valor nominal de flujo magnético, la optimización de energía previene pérdidas en el motor y así ahorra energía. El porcentaje promedio de energía que se ahorra en accionamientos de pequeño a medio tamaño, es del 3 al 5 % de la potencia nominal durante el funcionamiento a cargas reducidas, produciéndose además un beneficio adicional, y es que el motor gira casi sin ningún ruido, bajo pequeñas cargas para frecuencias de conmutación pequeñas y medias.

Funcionamiento a corriente límite

Los convertidores de frecuencia PWM en fuente de tensión, los cuales trabajan de acuerdo con una característica de control V/f simple, normalmente no son capaces de trabajar “suavemente” a corriente límite. Primero se reduce la tensión (y, entonces la frecuencia) hasta que se obtenga el valor límite de corriente. Tan pronto como se alcance este límite, el convertidor de frecuencia intenta conseguir de nuevo la referencia de velocidad (la tensión y la frecuencia se incrementan de nuevo). Esto conduce a un incremento o reducción de la velocidad, lo cual conlleva a una carga innecesaria, en particular sobre la mecánica del sistema, que puede tener un impacto negativo sobre la calidad del producto.

En la actualidad, los convertidores de frecuencia PWM usan una rampa interna, para buscar un punto de trabajo en el cual no se exceda el límite de corriente. En el caso de que se alcance la corriente límite, aparece una señal de peligro que avisa al operador. La frecuencia del convertidor no oscilará, a menos que no se pueda alcanzar una frecuencia adecuada.

Conclusiones

En lo que antecede, se ha realizado un análisis de las técnicas, estrategias y circuitos de control de la velocidad de los motores de inducción. En las últimas décadas, propiciado por el desarrollo de los microprocesadores digitales de señal (DSPs), con elevada potencia de cálculo y extraordinariamente rápidos, los cuales permiten incrementar la velocidad de respuesta y cálculo de los parámetros necesarios para los modelos y, también, utilizando nuevos dispositivos y técnicas de control, se ha tratado de conseguir que los motores asíncronos tuviesen el mismo comportamiento dinámico y nivel de precisión en el control que el de los motores de c.c. Así han surgido los métodos de control vectorial que tienen en cuenta la fase y utilizan un modelo complejo del motor que tiene en cuenta la orientación del campo magnético, lo cual permite actuar mejor sobre el par durante los transitorios y obtener así unas mejores prestaciones dinámicas.

Bibliografía

Magra, A.A. Accionamientos de velocidad variable & Soft Starters. Siemens, S.A., Agentina, 2003.

Fraile Mora, J. Máquinas eléctricas. 5ª Edición. McGraw-Hill, 2003.

Danfoss. General AC Theory. 2002.

Zamora Belver, I. Introducción a los accionamientos eléctricos de velocidad variable. E.T.S.I.I. Bilbao, 1995.

Pérez Donsión, M. y otros. Regulación de velocidad de motores eléctricos. Mundo electrónico, págs. 119-124. Nº 331. Mayo 2002.

Donsión, M.P. y otros. Regulación de velocidad de los motores eléctricos. Estado actual y perspectivas futuras (I), Energía, págs. 119-125. Nº 6. Noviembre/diciembre 2000.

Donsión, M.P. y otros. Regulación de velocidad de los motores eléctricos. Estado actual y perspectivas futuras (II). Energía, págs. 117-123. Nº 1. Enero/febrero 2001.

Donsión, M.P. y otros. Evolución de los motores eléctricos y su regulación de velocidad.

Actas de las 7as. Jornadas Hispano-Lusas de Ingeniería Eléctrica. Págs. 269-275. Madrid, julio 2001.