El sentido común de la producción industrial

Las empresas precisan un modelo productivo que permita amortizar de sus esfuerzos competitivos en términos de eficiencia operativa y de dominio del coste industrial

Desde la adopción de los acuerdos internacionales de libre comercio, se han incrementado de forma notable la competencia y la demanda, hechos a los que los medios productivos no se han adaptado adecuadamente. Una de sus manifestaciones más significativas ha sido el desplazamiento de capacidades productivas de occidente a los llamados “países emergentes”. Sin embargo, estas nuevas industrias reproducen, cuando no incrementan, las deficiencias de sus ubicaciones originales generando, además, graves repercusiones medioambientales. En consecuencia, su traslado a miles de kilómetros de la demanda refleja una solución momentánea a un asunto que no se ha resuelto satisfactoriamente hasta la fecha: el dominio del coste industrial a través de una fabricación eficiente.

La importancia de la reducción de los costes de explotación

En un entorno global de libre mercado en el que resulta difícil incrementar la cuota de mercado y/o diferenciarse de la competencia, uno de los principales retos empresariales es la maximización de los beneficios a través de la reducción de los costes y gastos de la cuenta de resultados.

Esta problemática es especialmente compleja en las empresas industriales, ya que el coste relativo a la construcción y entrega de la producción supone habitualmente un porcentaje importante de la facturación.

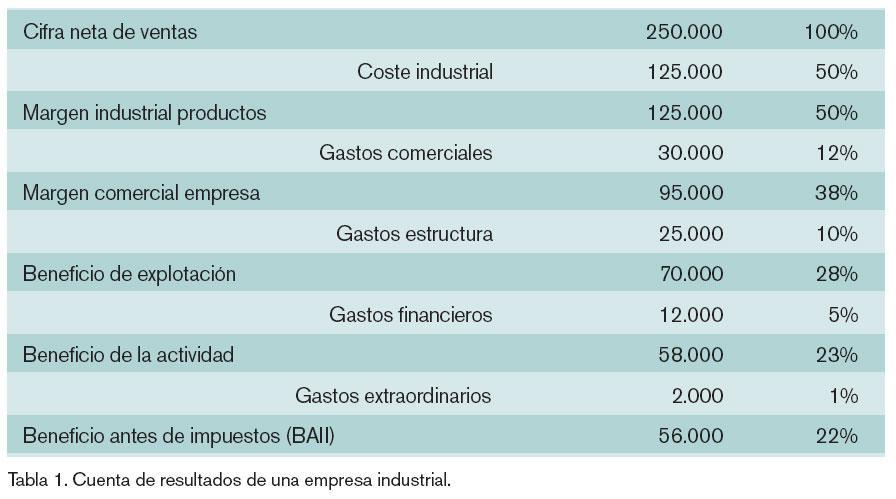
Por ejemplo, en la cuenta de resultados de la siguiente empresa industrial (tabla 1) se constata que cualquier reducción de los costes de explotación fuerza un efecto palanca de incremento del beneficio a través del factor obtenido al dividir el coste industrial entre el BAII, como se puede apreciar en la figura 1 (cuyo factor en este caso es del 2,23).

Las empresas son plenamente conscientes de ello y hasta suelen tener claro el volumen de reducción de costes necesario para garantizar la competitividad. La dificultad suele centrarse en la determinación del dónde y cómo realizarla sin mermar las condiciones de suministro de la demanda a corto o medio plazo.

¿Qué se espera de un proceso productivo?

Ya que resulta evidente la importante repercusión en el BAII de la reducción del coste industrial, cabe preguntarse ahora ¿qué se espera de un proceso productivo? ¿cuál es su objeto o finalidad? Y más aún, para un volumen concreto de coste industrial asociado a cierto período de tiempo, ¿cuál es el grado de cumplimiento de dicho objetivo por parte del proceso productivo?

La respuesta a la primera pregunta es más o menos obvia. De un proceso productivo se espera que satisfaga totalmente los requisitos de la demanda en términos de cantidad, calidad, coste y condiciones de entrega pactadas (en adelante, QCD).

Sin embargo, para la segunda pregunta, ni idea ¿verdad? Ciertamente, disponer de esa información haría considerablemente más fácil la cuantificación del rendimiento productivo necesario para satisfacer los requisitos estratégicos de reducción del coste, permitiendo actuar quirúrgicamente en las fuentes cruciales de deficiencia o mejora operativa. Pero sobre todo, permitiría saber dónde se encuentra el óptimo productivo de la empresa y hasta dónde se puede mejorar en las condiciones vigentes con independencia de las exigencias del mercado.

Paradójicamente, en la actualidad no existe ningún modelo comúnmente aceptado que cuantifique la eficiencia productiva de una empresa industrial. Lo cierto es que ni siquiera la consulta de la bibliografía más reputada sobre gestión empresarial es capaz de proporcionar una respuesta, siquiera teórica, al respecto. Más aún, se puede constatar la falta de consideración del proceso operativo como un elemento estratégico de primer orden.

Un buen ejemplo de esto último lo constituye la importante obra de Michael E. Porter Competitive Strategy, cuyo análisis descriptivo de la competitividad realizado ya hace casi 30 años no contempla las repercusiones de una empresa que cuente con un proceso de fabricación óptimo (o siquiera eficiente en cierto grado), y soluciona el tema con una proposición dicotómica simplificada que suena a algo así, si me permiten la analogía, “a elegir entre comer o beber, para alimentarse bien”. Desafortunadamente, éste no es el único caso.

Hace unos diez años, los autores de otra obra fundamental Cuadro de Mando Integral (Robert S. Kaplan y David P. Norton) apenas si dedicaron dos páginas al análisis del proceso productivo y menos de diez (sobre las 320 del total de la edición en castellano) a la definición de algunos parámetros genéricos.

Es cierto que desde la crisis del sector de la automoción norteamericana iniciada en los años 80 del pasado siglo se han hecho múltiples esfuerzos en este sentido, tanto a través de los procesos de normalización impulsados por las certificaciones internacionales o sectoriales como por la elaboración de diferentes modelos conocidos habitualmente por sus acrónimos: TQM, TPM, WCM, etc.

Si bien todos ellos han introducido importantes mejoras y proporcionado herramientas muy útiles, ninguno ha aportado la estandarización de un modelo integral de determinación del grado de eficiencia de un proceso productivo, ni han facilitado indicadores absolutos que impliquen el dominio del coste industrial.

En consecuencia, parece evidente el desconocimiento generalizado de los requisitos necesarios para conseguir el objetivo de la fabricación óptima o siquiera altamente eficiente en un proceso productivo y esto conlleva cierta desconsideración sobre su importancia estratégica.

Desde el inicio del capitalismo industrial (hace ya un par de siglos), las dos únicas vías de mejora “intuitiva” de la eficiencia productiva consisten en la reducción directa del coste industrial, “conseguir lo mismo por menos”, o el incremento del volumen a través de “conseguir más por lo mismo”.

Por tanto, puede que ahora se entienda mejor por qué los Consejos de Administración de las grandes empresas, compuestos en su mayoría por profesionales ajenos al entorno productivo, adoptan habitualmente decisiones de carácter defensivo al deslocalizar y aglutinar capacidades productivas en los países emergentes ante el incremento de la competitividad de los mercados.

De este modo, la primera hipótesis que debe ser asumida radica en el convencimiento de que un proceso productivo óptimo es un elemento estratégico fundamental para el posicionamiento competitivo de cualquier empresa industrial. Y será imprescindible que éste tenga una interacción adecuada con los procesos de innovación y comercialización aún en los casos en los que la principal ventaja competitiva sea mayoritariamente cualitativa, con la finalidad de reforzarla convenientemente.

Cabe preguntarse ahora qué impide a una empresa industrial, en el siglo XXI desarrollar sus procesos productivos de manera óptima cuando, por otra parte, muchas de las variables implicadas pueden ser y son de hecho regulables y existe una capacidad añadida específicamente constituida por los sistemas de información.

¿Qué es un proceso productivo óptimo en términos operativos?

Se puede entender que un proceso productivo tiene un rendimiento óptimo durante un período de tiempo finito en tanto que es capaz de satisfacer totalmente las necesidades específicas de su demanda en los términos anteriormente mencionados: QCD.

En consecuencia, cada factoría o empresa tendrá su propio nivel óptimo de respuesta en función de los requisitos particulares a satisfacer con su cuota de mercado.

De este modo, cualquier proceso productivo no óptimo, es decir, aquel que no alcanza a satisfacer todos los requisitos QCD, diremos que tiene cierto nivel de eficiencia asociado. Es decir, consigue satisfacer el óptimo esperado sólo en cierto porcentaje del mismo.

¿Qué necesita un proceso productivo para ser óptimo en términos operativos?

Básicamente, cualquier proceso productivo industrializado necesita desempeñar óptimamente tres funciones básicas: manutención, producción y logística.

Parametrización de la función de manutención

Se entiende por manutención aquellos procesos operativos encaminados a asegurar la presencia de las materias primas, consumibles, premontajes o cualquiera que sean las unidades de subproducto necesarias (en adelante, MM.PP.) para ser transformadas en el seno de la función productiva.

Desde un punto de vista óptimo, la manutención deberá asegurar que las MM.PP. estén siempre disponibles (cuantitativamente) y sean conformes (cualitativamente) para poder ser transformadas sólo cuando son requeridas por la demanda, o más exactamente, cuando el programa de producción emite sus necesidades inmediatas. Por tanto, será necesario:

1. Un stock de materias primas que satisfaga exactamente las necesidades cuantitativas de inmediata producción (sin rupturas ni excesos de inventario).

En efecto, cualquier proceso productivo, sea cual sea su naturaleza, requiere, si pretende ser óptimo, una disponibilidad cuantitativa exacta de los inventarios de MM.PP. frente a las necesidades de fabricación inmediatas. Cualquier desviación en la satisfacción de dichas necesidades tiene repercusiones operativas y/o financieras.

Por tanto, se puede definir la tasa de disponibilidad cuantitativa de la manutención (M₁ ) como el parámetro que mide el grado de eficacia del aprovisionamiento y determina el grado de adaptación del inventario de MM.PP. respecto a las necesidades inmediatas de producción, con el objetivo de garantizar una tasa de servicio del 100%.

Este elemento puede ser medido en cualquier empresa, independientemente de la frecuencia de emisión particular de su programa maestro de producción (diario, semanal…) obteniendo el cociente entre el inventario económico (referencia × cantidad × coste de compra unitario) de las MM.PP. realmente disponibles para su transformación y la explosión económica de las MM.PP. necesarias para satisfacer la demanda inmediata de producción (Bill Of Materials), asumiendo el criterio que un exceso o un defecto de la cantidad de existencias utilizables supondrá igualmente una tasa de servicio por debajo de la unidad.

2. Un stock de MM.PP. cualitativamente disponible al 100%

La experiencia demuestra que no sirve de nada un inventario perfectamente ajustado a las necesidades cuantitativas, si luego su consumo no satisface los requisitos necesarios para su adecuada transformación productiva.

En consecuencia, se puede definir la tasa de disponibilidad de MM.PP. conformes (M₂) como el cociente entre el montante económico de las MM.PP. consumidas por el proceso productivo en un período de tiempo y la suma de aquellas que no han sido rechazadas a lo largo de su proceso de transformación por falta de calidad.

Parametrización de la función productiva

Con dicho fin, se debe responder a la pregunta de: ¿qué necesita la función productiva para ser óptima? Dicha respuesta debe incluir ineludiblemente una disponibilidad total de los recursos técnicos y humanos para la fabricación durante la totalidad del tiempo de apertura del proceso productivo, piezas conformes “a la primera” con la cadencia prevista con el fin de permitir su posterior entrega al cliente en las condiciones pronosticadas. Por tanto, será necesario:

3. Un medio productivo disponible al 100% del tiempo de apertura

En efecto, el medio productivo debe estar siempre disponible para la producción independientemente de que éste sea utilizado o no en función de las necesidades de la demanda.

Por tanto, se podrá definir la tasa de disponibilidad del medio productivo (P₁ ) como el parámetro que mide el grado de eficacia del medio a través de la determinación del cociente entre el tiempo de apertura del proceso productivo y la disponibilidad temporal real del mismo en condiciones de fabricación de piezas conformes a la primera.

Para ello, en el cálculo de la disponibilidad real se deberán contabilizar todas las pérdidas temporales causadas por un funcionamiento no óptimo del mismo ocasionado por la existencia, por ejemplo, de macro y micro paradas (aquellas menores de un minuto) debidas a averías o accidentes, cambios de serie o reglajes, funcionamiento en vacío, protocolos de arranque y parada, o la producción no conforme.

4. Unos RR.HH. disponibles al 100% del tiempo de apertura para una fabricación óptima

De forma análoga a lo dicho para P₁, se puede definir a P₂ como la tasa de disponibilidad de la mano de obra directa (MOD), concretando este parámetro mediante la medición para cierto período de tiempo de la disponibilidad horaria real de los recursos humanos para una fabricación conforme y a la primera, dividido entre el tiempo bruto disponible teóricamente, observando para ello cualquier pérdida temporal bien sea por el desempeño de tareas no productivas, la producción no conforme, absentismo, accidentes laborales, permisos, descansos, etc. Es decir, contabilizando el tiempo teórico asociado a la producción conforme obtenida “a la primera” frente al total contratado para un determinado período de tiempo.

5. Una cadencia de producción ajustada el 100% del tiempo al estándar

Resulta fundamental para que un proceso productivo sea óptimo que la totalidad del tiempo de apertura del mismo se respete sin desviaciones de la cadencia de producción prevista teóricamente. Por tanto, se puede definir la Tasa de cadencia de la producción (P₃) en torno a la determinación del grado de estabilidad de la función productiva en la fabricación a la primera de productos conformes con las especificaciones. Tradicionalmente es un factor poco valorado en el mundo de la producción por cuanto se tiende a apreciar únicamente la eficacia en la fabricación del volumen de unidades previstas. Sin embargo, la cadencia es un elemento indicativo fundamental de la estabilidad productiva de un proceso de fabricación al requerir una sincronización óptima de los recursos implicados, garantizando con ello su repetibilidad y reproductividad (R&R) estadística. Es decir, condiciona la flexibilidad competitiva del proceso productivo global.

En consecuencia, es el indicador más importante del modelo por cuanto es el único que puede incrementar la eficiencia del proceso productivo en su totalidad a través de la reducción del estándar teórico del tiempo unitario de fabricación óptima del producto o Lead time.

Actualmente los sistemas de información permiten la obtención en tiempo real de esta información. Sin embargo, su precisión, naturaleza o incluso existencia es muy heterogénea en el mundo industrial. Por tanto, una sencilla aproximación al cálculo de dicho indicador consistirá en la obtención para un determinado período de tiempo del cociente entre el tiempo de apertura del proceso productivo y la suma de los tiempos teóricos de la producción conforme a la primera realizada en dicho período.

Parametrización de la función logística

Se entenderá por función logística los procesos operativos realizados desde que el producto ha sido fabricado en su totalidad hasta que es entregado al cliente. En consecuencia, el óptimo buscado será la entrega exacta de las unidades de producto demandadas en el plazo y condiciones estipuladas.

6. Un stock de producto terminado ajustado exactamente a las expediciones inmediatas

La propuesta es definir la tasa de flexibilidad de la función logística (L₁ ) como el cociente entre los montantes económicos de la disponibilidad real y teórica de las referencias pedidas en la cantidad y calidad adecuada para su expedición inmediata.

7. Una expedición del producto que satisfaga al 100% las condiciones de entrega pactadas con el cliente

Se puede definir entonces la tasa de servicio logístico (L₂ ) para un determinado período de entrega evaluado, como el cociente entre el montante económico de lo entregado cuando y como estaba previsto y las teóricamente previstas.

Obtención del rendimiento operativo global del proceso productivo

Como ya se mencionó anteriormente, una de las informaciones más valoradas en el seno del consejo de administración de una empresa industrial sería, probablemente, conocer en tiempo real el grado de eficiencia de las operaciones de su empresa. Es decir, tener una medida exacta del estado competitivo en el que se encuentra la estructura productiva reduciendo la incertidumbre en la toma de decisiones.

En consecuencia, si aceptamos que un proceso productivo específicamente óptimo es aquel que, mediante el consumo de los recursos previstos y disponibles en el momento adecuado, es siempre capaz de transformar y entregar los productos al cliente en el plazo y forma estipulada a la demanda. Y si admitimos que para cumplir dicho objetivo es necesario cumplir al 100% con todos y cada uno de los indicadores mostrados en el punto anterior, convendremos que la probabilidad de que todo esto ocurra en un determinado período de tiempo se podrá obtener mediante el productorio de las siete tasas anteriormente obtenidas.

De modo que el grado de eficiencia o tasa de rendimiento operativo global (R%) de cualquier proceso productivo en un período de tiempo finito se obtendrá como:

R% = M₁ × M₂ × P₁ × P₂ × P₃ × L₁ × L₂

Este resultado proporciona el grado de adaptación del proceso productivo respecto a los requisitos operativos de la demanda o, lo que es lo mismo, la tasa de producción fabricada con MM.PP. conformes, disponibles en la cantidad necesaria justo en el momento adecuado para ser transformadas de la manera especificada con los recursos previstos hasta su entrega al cliente en el plazo y forma estipulada. Todo lo demás, hasta la centena, por tanto, serán actividades productivas que han presentado alguna desviación en uno o varios de los parámetros definidos.

Interpretación del rendimiento operativo global obtenido de un proceso productivo concreto

Si en este punto el lector se ha molestado en calcular el nivel de eficiencia productiva de su empresa de acuerdo a este modelo, no se asuste, mis mediciones “oficiosas” a lo largo de mi experiencia profesional en factorías de varias multinacionales muy competitivas me indican que ninguna de ellas supera el 20%. De hecho, hay que pensar que si una empresa tuviera una tasa de eficiencia del 90% en cada uno de los parámetros evaluados, tan sólo obtendría un R% del 48%. Así que lo más probable es que su nivel de eficiencia esté por debajo del 1%.

Si se reflexiona acerca de este resultado, se concluye que el modelo permite conocer el origen de la fortaleza competitiva de una empresa. Y parece razonable pensar que aquellas empresas industriales cuyo rendimiento global sea mayor al porcentaje del BAII frente a la cifra neta de ventas tendrán su fortaleza competitiva mayoritariamente sostenida por sus procesos productivos.

En el caso de la empresa del ejemplo anterior, por el contrario, es la interacción de los procesos de innovación y comercialización la que “soporta” levemente el proceso operativo. Por tanto, la adopción del modelo de rendimiento operativo global debe generar reflexiones en el seno de la empresa con objeto de replantear la estrategia competitiva aplicando esta información. Máxime si se considera que este análisis también puede ser realizado a nivel externo permitiendo la comparación directa de una empresa con iguales o competidores sin perjuicio de que los rendimientos operativos puedan ser radicalmente diferentes fruto de una interacción distinta de sus procesos productivos ligados a sus ventajas cualitativas. En consecuencia, el benchmarking de rendimientos adquiere una dimensión más precisa sobre el origen de la fortaleza competitiva de la competencia.

Además, el modelo de rendimiento es útil para la determinación del nivel de eficiencia de una pequeña empresa, una factoría industrial, o cualquier organización humana con una finalidad productiva, y es aplicable tanto en la toma de decisiones sobre la totalidad del negocio como en la operación más cotidiana en el seno de una determinada función operativa.

En efecto, muchas de las deficiencias del rendimiento son generadas por la existencia de un efecto en cascada a lo largo del proceso productivo desde la manutención hasta la logística, por el que las pequeñas desviaciones de la primera pueden generar importantes perturbaciones logísticas. En este sentido, el diagrama de rendimientos constituye en sí mismo un DAFO del proceso productivo, aportando información sobre la localización y las consecuencias asociadas de los problemas en términos de eficiencia.

Esta circunstancia, por cierto, corrobora el hecho de que la única opción de supervivencia operativa de una empresa radica en la cooperación entre las diferentes unidades organizativas que la componen, ya que la falta de eficiencia en el cumplimiento del objetivo de una de las funciones afecta gravemente al conjunto.

Repercusión económica del modelo de rendimiento global operativo del proceso productivo

El indicador de rendimiento global operativo no mostraría todo su alcance si no contemplara las implicaciones económicas de la eficiencia productiva. Afortunadamente, la vinculación es sencilla y directa, ya que en un período de tiempo se puede conocer el nivel de eficiencia productiva y asociarlo al coste de explotación incurrido en ese mismo período, por lo que fácilmente se puede saber el volumen total del coste industrial empleado en sufragar desviaciones por ineficiencia.

Veámoslo con el ejemplo de la empresa anterior, para lo cual suponemos un diagrama de rendimientos como el mostrado en la tabla 2:

Dicho diagrama proporciona un rendimiento productivo global (R%) del 18%. En consecuencia, si este resultado se vincula a los costes industriales de la cuenta de resultados (tabla 1) multiplicándolo, se obtendrá el volumen del coste industrial empleado eficientemente: 22.500 unidades monetarias (UM), o lo que es lo mismo, se tendrá la valoración de los costes industriales sin valor añadido, 102.500 UM.

Este último aspecto es tremendamente importante, ya que si se considera que en la empresa del ejemplo el 82% del coste industrial es empleado en actividades ineficientes, en el hipotético caso de la eliminación de la totalidad de las ineficiencias sin necesidad de inversiones y la obtención, en consecuencia, de un rendimiento productivo (óptimo) del 100%, repercutiría en los resultados económicos con un incremento del BAII superior al 280%, lo que fortalecería considerablemente su posición en el mercado.

Qué hacer con el modelo de rendimiento global del proceso operativo

Una acción implícita a la aplicación práctica del modelo es la adecuación del sistema de información de la empresa con el fin de poder obtener datos en tiempo real con la suficiente precisión sobre la evolución de los distintos parámetros de control del rendimiento. Por motivos análogos, el coste industrial deberá ser igualmente monitorizado con la suficiente sensibilidad como para recoger las desviaciones presupuestarias que produzca la “manipulación” del rendimiento operativo.

Dicho lo cual, a efectos de mostrar el uso práctico del modelo de rendimiento global, será necesario retomar la cuenta de resultados y el diagrama de rendimientos de la empresa del ejemplo (tablas 1 y 2).

Se ha de revisar la estrategia

Como se puede apreciar en la empresa del ejemplo, para un rendimiento global del 18%, el coste industrial en operaciones no eficientes supone 102.500 UM (82% del coste industrial). Parece ineludible, pues, que la revisión del plan estratégico sea el primer paso a ejecutar con la finalidad de incluir en él las informaciones que este nuevo escenario proporciona, estableciendo objetivos más acordes con el mismo.

En el ejemplo, se aprecia cómo la interacción de los procesos de innovación y comercialización “soporta” el proceso operativo, al tener respectivamente un rendimiento global del 18% y una tasa de BAII sobre las ventas netas del 22%.

Por tanto, será interesante evaluar a la competencia en los mismos términos, al objeto de averiguar el origen de su fortaleza competitiva. Sólo de este modo es posible definir una estrategia adecuada que defina la interacción más adecuada de los procesos proporcionando el nivel de competitividad deseado.

Se ha de revisar la táctica

La aplicación del modelo exige que la revisión de la táctica contemple la determinación concreta de dos objetivos básicos. El primero de ellos lo constituye la definición del volumen de transformación deseada del coste industrial ineficiente (sin valor añadido) en beneficio, en términos de máxima eficiencia con la mínima inversión. El otro objetivo fundamental consistirá en delimitar el grado de “variabilización” del coste industrial eficiente necesaria con el fin de aumentar la flexibilidad del proceso productivo ante las oscilaciones de la demanda.

Dicha revisión, además de la política estratégica de la empresa, también ha de considerar dos principios básicos ligados a la implantación del modelo. El primero de ellos persigue la armonización de las tasas de servicio de las funciones internas del proceso operativo, ya que sus diferencias previsiblemente fomentan la existencia de tensiones internas en el seno de la organización y la desequilibran operativamente. El segundo principio tiene que ver con la propia definición del proceso operativo, por cuanto la eliminación de las deficiencias propias de cualquier función repercute en la mejora del rendimiento de las funciones inmediatamente consecutivas. Como consecuencia de ello, la función de manutención deberá ser la que conlleve un esfuerzo prioritario de mejora de la eficiencia.

Como información complementaria, parece interesante contemplar las implicaciones económicas de las diferentes políticas de eliminación de deficiencias posibles a corto y largo plazo.

De este modo, continuando con el ejemplo anterior, se supone ahora que todos los demás elementos de la cuenta de resultados permanecen constantes durante dicho período de forma que mientras el rendimiento aumenta, de forma simultánea, el coste industrial se reduce sin necesidad alguna de inversiones para ello. Una primera aproximación será la simulación de la eliminación de deficiencias a largo plazo, es decir, asumir la creación de un programa cuya aplicación en un determinado período de tiempo conlleve conseguir el pleno rendimiento (R% = 100%). De esta manera se pasará de un rendimiento del 18% en el año N hasta alcanzar el 100% en N+10.

Con este fin, se ha confeccionado el gráfico de la figura 2 que compara la evolución de los costes industriales en función de dos políticas distintas de eliminación de deficiencias. En una de ellas, la mejora del rendimiento es paulatina y en la otra es aleatoria y creciente (es decir, el rendimiento de un período nunca es menor al del período anterior).

Como se puede observar, el sistema tiende a un mínimo muy parecido, y mientras la política de mejora “paulatina” consigue el pleno rendimiento en el año N+10 con un coste industrial de 52.652 UM (58% de reducción desde N), la política de mejora sostenida “aleatoria” lo hace a un coste un 4% menor. En este sentido, si se realiza el sumatorio de los costes industriales asociados a la vigencia del programa de mejora, correspondientes a cada política, se aprecia que el programa “paulatino” ha supuesto un gasto superior de 14.000 UM. En consecuencia, dado un período de tiempo prolongado en el que se pretenden eliminar las deficiencias por completo, es globalmente más beneficioso exceder la mejora lineal del rendimiento.

Por otra parte, los datos experimentales confirman que la eliminación total de las deficiencias del sistema productivo en el menor período de tiempo posible proporciona la máxima eficiencia productiva al mínimo coste industrial. Ya que, en la empresa del ejemplo, el coste industrial se sitúa en 22.118 UM (reducción del 82%) y el BAII se eleva hasta las 151.695 UM (incremento mayor del 280%) si la optimización se realiza en un solo período de tiempo (figura 3).

Se han de modificar las operaciones

Una vez definidos los objetivos de mejora cruciales, se debe evaluar el diagrama de rendimientos de la empresa con el fin de definir el nivel de progreso necesario de los parámetros específicos de cada función operativa. Y, a continuación, hay que preguntarse por qué se han producido las deficiencias en cada uno de ellos.

Atendiendo a Pareto, y de no existir ningún “cáncer” (entendiendo por este término un parámetro cuya tasa de eficiencia esté muy por debajo de la media), cualquier empresa estará en condiciones de eliminar un 80% de sus deficiencias solventando unos 21 asuntos. Éstos, probablemente, se corresponderán con las causas de dos o tres graves problemas operativos globales, ocultos y no resueltos hasta la fecha.

En estos momentos, por tanto, ya se pueden prever ciertos aspectos fundamentales a tener en cuenta en la puesta en práctica operativa del modelo de rendimiento global y de los planes de acción necesarios.

1. Es imprescindible contar con un sistema de información que proporcione datos precisos del nivel de rendimiento y coste industrial al objeto de tomar a tiempo la decisión más adecuada, máxime si se empiezan a hacer cambios operativos.

2. El tiempo empleado en la mejora del rendimiento es un factor crucial, por lo que la organización debe estar unívocamente concienciada en este sentido.

3. La mejora del rendimiento es imposible sin la acción cooperativa y autocrítica de todos los agentes implicados (incluyendo externos), por lo que se deberán revisar y reformar los canales de comunicación vertical y horizontal existentes.

4. El análisis de las deficiencias debe ser realizado en términos de atributos óptimos y no en el análisis exclusivo y minucioso de datos, ya que ésta es una deformación profesional muy común de los técnicos.

5. La organización debe ser más flexible para permitir la libre opinión y la toma de decisiones, asumir la comisión de errores (en muchos se tratará de probar soluciones) y proveer los recursos necesarios en los plazos previstos en los planes de acción. Se necesita liderazgo.

6. Muchas de las deficiencias son fácil y rápidamente resolubles al ser originadas por la existencia de procedimientos anacrónicos, falta de comunicación o información, una inapropiada distribución de los recursos o por la dilación burocrática en compras plug and play.

7. La erradicación de algunas deficiencias complejas (por su causalidad multivariable) o las mejoras de estándares que supongan la eliminación de restricciones específicas del proceso productivo a través de desarrollos tecnológicos concretos requieren períodos prolongados de tiempo y la colaboración transitoria de agentes externos. En consecuencia, la organización debe ser capaz de gestionar estos proyectos con eficacia.

8. Las funciones complementarias del proceso operativo deben adecuar su rendimiento al del proceso operativo ofreciendo sus servicios a un coste totalmente variable.

Ejemplo práctico

Supongamos que en el ejemplo de la empresa industrial anterior la dirección ha considerado prioritaria la mejora de la tasa de disponibilidad de producto terminado (L₁ ) hasta un mínimo del 70%, eliminando con ello un exceso de inmovilizado económico.

En consecuencia, el siguiente paso es evaluar las causas de ineficiencia en el indicador. Para lo cual se cuenta con un diagrama de Pareto (figura 4) que muestra las referencias con mayor volumen económico de inventario por encima de las necesidades inmediatas:

En efecto, se puede observar un caso común en que las tres principales referencias de inventario excesivo aglutinan el 70% de las deficiencias de L₁. Por lo tanto, su completa eliminación supondría incrementar la eficiencia del indicador hasta el 88% superando con ello el objetivo propuesto.

En tal caso, es necesario analizar ahora el origen del exceso de inventario de dichas referencias y sus repercusiones en los demás parámetros del modelo (si las hubiera).

Supongamos ahora, como conclusión a dicho análisis, un caso habitual en las empresas industriales consistente en el hecho de que dichas referencias pertenecen a una familia de producto que es fabricada en una misma línea productiva, la cual, dada su antigüedad, requiere una gran cantidad de tiempo de ajuste tanto en su arranque como en su parada. En consecuencia, el equipo de producción fabrica unidades en exceso siempre que puede con el fin de minimizar los ajustes del medio y mejorar su productividad. De modo que el rendimiento de P₁ es afectado únicamente en un 10% por estas referencias. Sin embargo, este hecho también causa afecciones en la función de manutención por cuanto se amplía la dispersión del consumo de las MM.PP. necesarias, alterando sus previsiones y provocando una pérdida de eficiencia en M₁ del 10% por un inventario excesivo.

Una vez definida la causa raíz de la deficiencia y localizadas cuantitativamente las pérdidas de rendimiento que acarrea para las funciones operativas, es el momento de valorarla en términos económicos, asumiendo que la cuenta de resultados del período N+1 es exactamente igual a la de N mostrada en la tabla 1.

Para ello, en primer lugar, se deberá recalcular el rendimiento productivo de la empresa incorporando la mejora que supondría la desaparición de la misma, tal y como se puede observar en la tabla 3.

De esta manera, la simulación de la desaparición de la deficiencia y el incremento del rendimiento de M₁, P₁ y L₁, mejoraría el rendimiento global operativo de la empresa hasta el 33% (frente al 18% anterior), estando ya en condiciones de realizar la valoración económica de dicho incremento. Para lo cual se evalúa la repercusión en el período N de un rendimiento del 33% y, con tal fin, se nombra a ese año como N* confeccionando la siguiente tabla (tabla 4):

En efecto, se observa cómo el incremento del rendimiento supone una variación neta de costes de 18.939 UM ya que los empleados eficientemente aumentan en esa cantidad, mientras que los costes sin valor añadido descienden exactamente en la misma cantidad respecto al cálculo para un rendimiento global del 18%.

La razón de ello es sencilla si se asume que el coste de cualquier deficiencia se descompone en un factor eficiente y otro de desviación del estándar. En este caso, al mantenerse el coste industrial constante, la igualdad supone que las 18.939 UM se emplean en su totalidad en el aumento eficiente del rendimiento hasta el 33%

Naturalmente, el grado de apalancamiento financiero de la empresa distorsionará esta estimación. En consecuencia, simultáneamente será necesario realizar esfuerzos concretos de minimización y/o variabilización de los costes asociados a la deficiencia.

En función de este resultado se puede afirmar que la repercusión económica de la eliminación del 70% de las deficiencias de L₁, y el 10% de M₁ y P₁ puede reducir los costes industriales en 19.939 UM (15%) e incrementar el BAII hasta las 74.939 UM (34%).

En consecuencia, las funciones de manutención, producción y logística ya están en condiciones de elaborar cooperativamente planes de acción que aseguren en la mayor brevedad de tiempo posible la obtención de las mejoras previstas en M₁, P₁ y L₁ con una inversión inferior a 19.939 UM, adoptando reformas internas que produzcan una eliminación o variabilización total o parcial del incremento de dicho coste eficiente independientemente del ahorro producido por la supresión de la deficiencia del rendimiento.

Más allá del rendimiento óptimo…

Es evidente que cada proceso operativo tiene un nivel de eficiencia específico que no tiene por qué coincidir con el óptimo y, en algunas ocasiones, incluso un rendimiento global pleno no es suficiente a largo plazo desde el punto de vista estratégico y/o competitivo. Por tanto, es necesario realizar cambios que puedan suponer modificaciones más o menos importantes del medio productivo, el producto o la reducción del lead time (P₃). En este caso, el verdadero reto será mantener dicho nivel de rendimiento pleno, ya que cualquier mejora de cualquier estándar (incremento de su exigencia) provocará repercusiones en el conjunto del proceso productivo en forma de aparición de deficiencias.

Conclusiones

Como se ha podido comprobar, la inexistencia de un modelo de control de la eficiencia del rendimiento de las operaciones realizadas en el seno de los procesos productivos industriales conlleva una serie de consecuencias que van desde su desconsideración estratégica hasta la adopción generalizada de decisiones empresariales erróneas ante el incremento de la competencia.

En virtud de esta ocurrencia, el presente modelo pretende dar una solución a esta problemática, proporcionando una vía de mejora a las empresas que garantice la armonización de sus esfuerzos competitivos tanto en términos de eficiencia operativa como de dominio del coste industrial.

Uno de los retos más sobresalientes que aporta la implantación del modelo de rendimiento global operativo lo constituye el hecho de que el proceso productivo no tiene por qué organizarse funcionalmente de manera simétrica. Por el contrario, cada función o unidad organizativa debe especializar sus recursos con el fin de optimizar su propia eficiencia, y esta estructura singular debe evolucionar autónomamente de acuerdo con el cumplimiento de sus exigencias específicas.

Por otra parte, la puesta en marcha de los planes de acción necesarios para el incremento del rendimiento requiere un estricto control presupuestario de las inversiones y su repercusión en el coste industrial.

Por lo que es de prever la necesaria creación de cuentas de explotación específicas para cada una de las funciones o unidades productivas de la empresa. Esta evolución, acrecentada por la presión de la competencia, provocará que algunas unidades funcionales sean incapaces de asumir la competitividad necesaria y/o los recursos necesarios sean demasiado cuantiosos, lo que desembocará en una externalización total o parcial de las mismas.

Por tanto, es previsible que la empresa industrial eficiente del futuro se constituya como una agrupación cooperativa de empresas que explotan un determinado negocio de construcción y entrega de productos.

Por último, si se puede extraer una conclusión general de todo el desarrollo, ésta se fundamenta en la importancia clave de los activos intangibles en la garantía de la competitividad, ya que el modelo permite definir las vías de actuación para que las personas apliquen de forma cooperativa todo su potencial creativo en la mejora del rendimiento dela empresa, constituyendo la verdaderaventaja diferencial frente a la competencia.

Epílogo

El presente artículo sólo trata de mostrar una información empírica abierta al análisis y discusión de los profesionales, con la finalidad exclusiva de fomentar su puesta en práctica inmediata.

Por tanto, los escépticos están de enhorabuena, ya que deliberadamente en este artículo no existe ninguna intención de demostrar la validez teórica del modelo, evidenciar exactamente sus fundamentos, ni analizar pormenorizadamente las consecuencias teóricas propias de su adopción masiva en el sector industrial. Éstos son aspectos que, o bien escapan a las competencias e intereses del autor, o al presente ámbito de expresión.

Sin embargo, sí que recomendaría encarecidamente la reflexión sobre las implicaciones energéticas de la aplicación del modelo en términos de reducción de los consumos energéticos industrial y difuso, y las emisiones de CO₂ asociadas. Mis estimaciones personales a este respecto, sinceramente, me abruman.

Quizá entonces la solución del problema climático sólo necesite de un poco de sentido común.

Bibliografía

Kaplan, Robert. S.; Norton, David P. (1997). El cuadro de mando integral, Ed. Gestión 2000

Porter, Michael E.; (1980). Competitive strategy. Techniques for analysing industries and competitors, Ed. The Free Press