El diseño paramétrico como herramienta creativa en diseño de producto
Parametric design as a creative tool in product design
Aitor Lekuona Amundarain (1), Manuel Domínguez Somonte (2) y María del Mar Espinosa Escudero (3)
Resumen
La corriente paramétrica nace en respuesta a la necesidad de la singularidad y diversidad en diseño y arquitectura. El diseño paramétrico describe los modelos mediante geometrías con parámetros asociados y representa la relación dentro de la geometría del producto. Con el diseño paramétrico como herramienta, el diseñador ya no diseña un producto estrictamente, sino que crea el código paramétrico que diseñará el objeto en cuestión. La variabilidad paramétrica del código hace de estos modelos herramientas muy poderosas de generación e innovación en diseño. Este artículo pretende explorar las bases del diseño paramétrico, las herramientas digitales empleadas y la lógica de diseño asociada, así como su potencial y las limitaciones como herramienta avanzada en diseño de producto para impulsar la creatividad del diseñador. Las herramientas paramétricas han permitido incrementar la creatividad durante el modelado y mejorar la diversidad, rapidez y calidad de estos diseños, además de ser el catalizador para el diseño generativo. No obstante, sus limitaciones residen en la capacidad de manejo de la herramienta por parte del diseñador, así como las restricciones de fabricación actuales.
Palabras clave: Diseño paramétrico, diseño variacional, software paramétrico, lógica paramétrica, creatividad.
Abstract
Parametric movement was born in response to the need for uniqueness and diversity in design and architecture. Parametric design models are described by means of geometries with associated parameters and also represent the relationship within the overall product geometry. With parametric design as a tool, the designer no longer strictly designs a product, but creates the parametric code that will design the object in question. The parametric variability of the code makes these models very powerful tools for design generation and innovation. This article aims to explore the fundamentals of parametric design, the digital tools used and the associated design thinking, as well as its potential and limitations as an advanced tool in product design to boost creativity. Parametric tools have improved creativity and diversity in CAD, and the quality and speed of these designs. Parametric design has also act as the catalyst for what is today known as generative design. However, its limitations lie in the designer’s ability to handle the tool, as well as current manufacturing process restrictions.
Keywords: Parametric design, variational design, parametric software, parametric thinking, digital creativity.
Recibido / received: 23/02/2021. Aceptado / accepted: 15/06/2021.
1 Máster en Ingeniería Biotecnológica por la Universidad Técnica de Dinamarca (2016). Estudiante del Máster Universitario en Ingeniería del Diseño en la Universidad Nacional de Educación a Distancia (UNED).
2 Profesor de la Escuela Técnica Superior de Ingenieros Industriales de la Universidad Nacional de Educación a Distancia (UNED), en el Departamento de Ingeniería de Construcción y Fabricación. Profesor del Máster Universitario en Ingeniería del Diseño. Universidad Nacional de Educación a Distancia (UNED).
3 Profesora de la Escuela Técnica Superior de Ingenieros Industriales de la Universidad Nacional de Educación a Distancia (UNED), en el Departamento de Ingeniería de Construcción y Fabricación. Profesora y coordinadora del Máster Universitario en Ingeniería del Diseño. Universidad Nacional de Educación a Distancia (UNED).
Autor para correspondencia: Aitor Lekuona Amundarain; e-mail: alekuona3@alumno.uned.es.
Introducción
El término ”paramétrico” tiene su origen en el griego, que etimológicamente significa “medir, comparar distancias”, y de ahí ha pasado a la ciencia de las matemáticas, y más en concreto a las ecuaciones paramétricas (Christodoulou, 2020). Estas emplean variables independientes (denominados parámetros) en las que las variables dependientes se definen como funciones continuas del parámetro y no dependen de otra variable existente. Los inicios en expresar geometrías con ecuaciones paramétricas se dan en la primera mitad del siglo XIX, cuando James Dana explica las geometrías de cristales con parámetros, variables y ratios (Davis, 2013). Las primeras aplicaciones prácticas datadas se dan entre otros por Antonio Gaudí en el uso de las geometrías paramétricas para diseñar arquitectura (Christodoulou, 2020) (Eltaweel, SU, 2017) (Barrios Hernandez, 2006).
La arquitectura paramétrica es un método de diseño que se basa en parámetros predefinidos que sirven para controlar las relaciones entre ellos y así definir una geometría. Pieter Bruegel, pintor renacentista holandés, describió y representó la torre de Babel como unedificio que redefine constantemente sus necesidades, a medida que crece y se vuelve más complejo (Schnabel, 2012). Este concepto de edificio hoy en día es posible gracias a la incorporación de reglas de diseño paramétrico en arquitectura, donde los arquitectos no prescribieron una definición fija de arquitectura, sino un conjunto de reglas e instrucciones que informan y pueden generar el resultado.
En materia de diseño paramétrico, el diseñador define algunos parámetros dentro de los cuales puede ajustar y controlar la geometría de su trabajo (Bhooshan, 2017). Fueron los avances relacionados con el diseño asistido por ordenador los que permitieron establecer las bases de lo que hoy en día se conoce por diseño paramétrico (Christodoulou, 2020) (Schumacher, London, 2008). Según Patrick Schumacher, el estilo paramétrico nace en respuesta a la necesidad de singularidad y diversidad impulsada por una sociedad heterogénea, con demandas más complejas para la arquitectura y el diseño (Schumacher, London 2008). Hoy en día, los diseñadores contemporáneos tratan con algoritmos como modelo de cálculo para realizar sus tareas de diseño (Khabazi, 2012).
Desde un punto de vista de la lógica del diseño, el diseño paramétrico se define como un proceso de exploración de las relaciones asociativas de conceptos geométricos (Oxman, 2017) (Geren, Akçal? et al., 2017). El modelado paramétrico asociado al diseño paramétrico permite describir los modelos mediante geometrías con parámetros asociados y representar la relación dentro de la geometría del producto (Geren, Akçali et al., 2017) (Alcaide-Marzal, Diego-Mas et al., 2020) (Barrios Hernandez, 2006). Las herramientas paramétricas nos permiten reflexionar sobre la lógica asociativa y la geometría de las formas generadas en el software paramétrico, además de explorar alternativas modificando los parámetros. Cuando se modifica el valor de un parámetro (por ejemplo, una dimensión), este cambio se propaga a los otros parámetros a través de estas relaciones.
En cuanto a la interfaz de diseño, la gran ventaja es la pantalla visual proporcionada para apoyar el curso del diseño del objeto algorítmico durante la generación y modificación paramétrica (Oxman, 2017). En cuanto a la obtención de los diseños paramétricos, la necesidad de los ingenieros de fabricar geometrías complejas los llevó al desarrollo e implementación de herramientas de fabricación digital para estos diseños (Christodoulou, 2020). Las máquinas de fabricación digital, ampliamente establecidas hoy en día, han permitido la programación y fabricación de productos directamente a partir de diseños paramétricos digitales. Las diferentes formas de fabricación digital (control numérico, impresión 3D, corte por láser, etc.), así como la aparición de nuevos materiales afines a estos sistemas productivos, han permitido llevar a cabo diseños con geometrías paramétricas antes no vistas en infinidad de campos.
Hoy en día, el diseño paramétrico se utiliza en muchos campos en los que la metodología de diseño consiste en relaciones algorítmicas complejas, trabajo interdisciplinario y creatividad (Eltaweel, SU, 2017). Controlar todas estas operaciones con herramientas convencionales no es fácil, por lo que es necesario utilizar sistemas operativos complejos, herramientas paramétricas y software específico. La evolución en este campo del diseño ha permitido avanzar e implementar el diseño paramétrico en campos como: diseño de producto, diseño de interiores, arquitectura, planificación urbana, análisis estructural, moda y otros tantos (Oxman, Gu, 2015).
etapa. Adaptada de Eltaweel, SU, 2017.
Modelos paramétricos
Desde la llegada de los sistemas de diseño asistido (DA), la importancia del software es vital en materia de diseño y arquitectura (Agirbas, 2020). Estas herramientas digitales son capaces de ejecutar formas en línea con el diseño contemporáneo con facilidad, rapidez y variedad, que de otro modo sería imposible. No obstante, los avances en materia de softwares se están desarrollando velozmente, y también afectan a la cantidad de programas disponibles. Si bien la informatización fue el primer paso, la utilización de softwares ha evolucionado hacia la era de la computación en los procesos de diseño, y ha afectado también a la manera de pensar el diseño (Khabazi, 2012). Tanto las herramientas como la interfaz de cada software son distintos, por lo que hay una necesidad por parte del diseñador de familiarizarse y adaptar su manera de pensar y ejecutar en cuanto a diseño (Alcaide-Marzal, Diego-Mas et al., 2020) (Oxman, Gu, 2015).
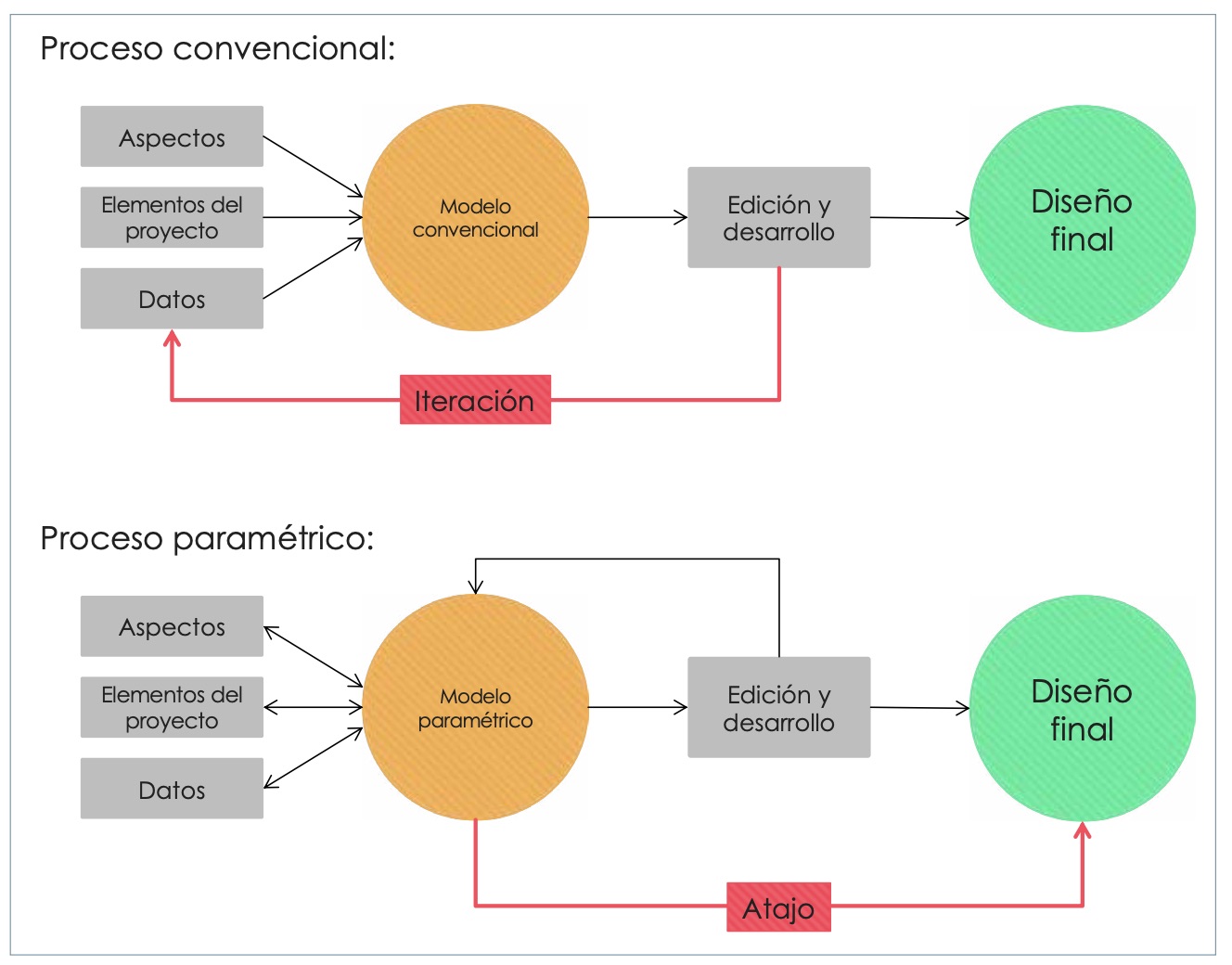
En la manera convencional de diseñar por ordenador, una vez el modelo inicial es creado, cualquier cambio supone repetir el proceso de diseño, lo cual exige mucho tiempo (Eltaweel, SU, 2017) (Fig. 1). En diseño paramétrico, no obstante, se emplean herramientas de software capaces de cambiar y mejorar los diseños eficientemente, ya que integran y coordinan varios componentes de diseño simultáneamente. Esto supone que la modificación de cualquier parámetro automáticamente actualizará el modelo en cuestión, con lo que el diseñador debe estar familiarizado con lógica, el software y el proceso paramétrico (Barrios Hernández, 2006). El proceso de búsqueda del diseño final por medio de modelos involucra tres etapas clave: 1) creación del boceto inicial, 2) incorporación de restricciones y 3) resolución del modelo (Shah, 2001).
Durante la fase de creación de boceto, el diseñador debe aplicar una lógica paramétrica. Una línea, por ejemplo, pasa a formar parte de un modelo una vez que se especifican dos parámetros, su longitud y su dirección (Anderl, Mendgen, 1996). Mediante la modificación de cualquiera de los parámetros, la forma primitiva será modificada. Partiendo de entidades primitivas parametrizadas, los sistemas DA permiten crear elementos complejos estableciendo las relaciones entre estas entidades. De este modo, se obtienen formas complejas capaces de hacer variar fácilmente mediante la modificación de cualquiera de los parámetros primitivos.
Durante la fase de incorporación de las restricciones, estas establecen vínculos lógicos y paramétricos entre elementos del modelo (paralelismo, contacto, distancia, etc.), limitando el comportamiento de las entidades involucradas. La creación de las restricciones puede ser más manual o automatizado por el sistema dependiendo del software en uso.
La introducción de restricciones en DA implica, del mismo modo, la noción de grado de libertad, y modelos sobrerrestringidos y subrestringidos. Cada vez que el diseñador introduce una restricción al modelo, el grado de libertad de este disminuye hasta el punto de sobrerrestringirlo si se introducen demasiadas restricciones, eliminando la posibilidad de cualquier variación de diseño.
Desde un punto resolutivo, los modelos paramétricos en DA están gobernados por un set de ecuaciones caracterizado por variables y restricciones. Dependiendo de la estrategiade resolución del modelo, se puede diferenciar en un enfoque paramétrico o variacional. El software estrictamente paramétrico se resuelve modelo con un enfoque secuencial, donde cada ecuación se resuelve una tras otra hasta determinar todas las variables. Por el contrario, en el diseño variacional hay una resolución simultánea. Además, los sistemas variacionales permiten una resolución de modelos subrestringidos, con lo que proporcionan varias alternativas de solución. Esto permite mayor flexibilidad y productividad al diseñador, ya que no tiene por qué definir completamente todas las restricciones y proporciona mayor variedad de soluciones.
Los sistemas estrictamente paramétricos no apoyan la evaluación de las alternativas de diseño (basadas en grados de libertad, es decir, bajo geometría restringida) como lo hacen los sistemas con soluciones variacionales. No obstante, ambos conceptos están estrechamente ligados, lo que causa muchas veces la confusión en el uso de estos términos. Hoy en día, la mayoría de los sistemas de DA denominados paramétricos funcionan con solucionadores variacionales. Estos sistemas varían en la forma de presentar las alternativas de diseño e interactuar con el diseñador. Desde la aparición de la primera herramienta paramétrica en 1987 por la compañía Pro/ENGINEER, el ahora llamado PTC Creo, cada compañía de DA ha desarrollado su propio software paramétrico. CATIA, SOLIDWORKS, Autodesk Inventor, Creo Parametric, Siemens NX y Grasshopper de Rhinoceros son algunos ejemplos (Geren, Akçali et al., 2017).
En estos softwares, el diseñador crea una estructura conceptual que oriente las variaciones de los parámetros. Esto requiere un enfoque en el que se invierta tiempo en una etapa intermedia entre la idea y el diseño (Stals, Jancart et al., 2020). El “diseño” del algoritmo, o código, precede la generación de la forma, en la que el diseñador produce la descripción algorítmica del diseño previsto, incluida la lógica y las dependencias entre los parámetros de entrada y las operaciones geométricas dependientes. Cuando se cambia el valor de un parámetro, la modificación se propaga con relación a las dependencias del parámetro modificado, induciendo a los parámetros dependientes a adaptarse automáticamente (Barrios Hernández, 2006).
El cambio en el proceso de diseño va muy ligado de la mano de un cambio cognitivo de pensamiento y lógica de diseño. Se podría interpretar, por tanto, que el diseñador ya no diseña un objeto o edificio, sino que diseña un proceso. Es por eso por lo que el diseño paramétrico permite explorar más allá de las ideas originalmente previstas, incrementando así la creatividad, en contraste con el enfoque de las herramientas tradicionales DA (Eltaweel, SU, 2017). La investigación en lógica de diseño ha demostrado que los medios digitales y los métodos de trabajo tienen una gran influencia en la manera de pensar del diseñador (Oxman, 2008). Por ello es importante entender la forma en la que los distintos softwares paramétricos apoyan el pensamiento paramétrico del diseñador (Aish, Hanna, 2017).
Pensamiento y lógica paramétrica
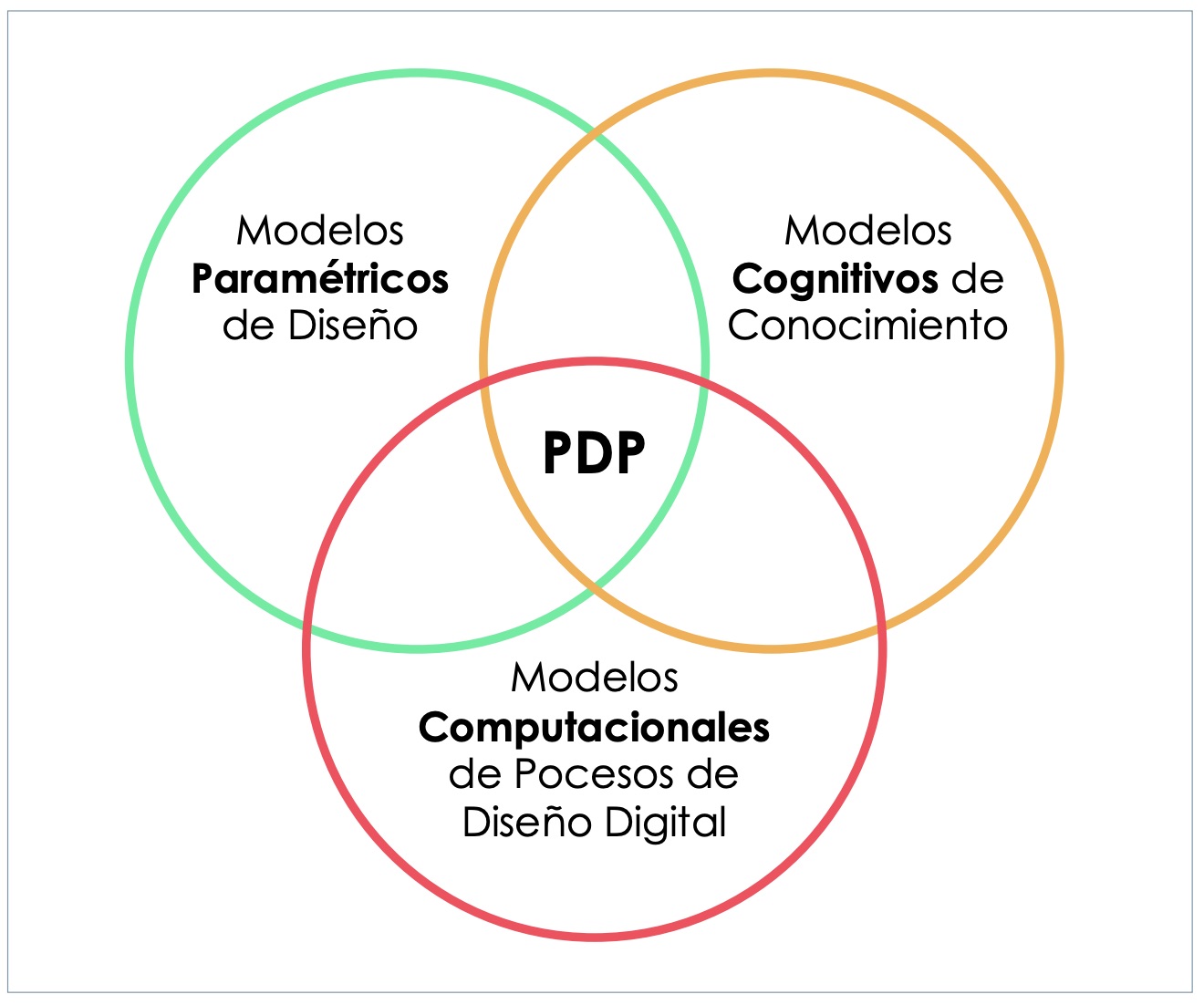
Más allá de ser otra herramienta de modelado de formas complejas, el diseño paramétrico está emergiendo como un modelo de diseño distintivo (Oxman, 2017). Debido a esto, los diseñadores deben pensar sobre los problemas relacionados con el diseño de distinta manera a la tradicional, incluso creando una filosofía paramétrica (Schnabel 2012) (Oxman, Gu, 2015). El diseño paramétrico se basa en el pensamiento algorítmico, el cual se puede definir como: un conjunto de reglas escritas por un código fuente de instrucciones explícitas que inician procedimientos computacionales que generan formas digitales (Oxman, 2017). Desde un punto de vista de la lógica de diseño, el diseño paramétrico, se basa en el proceso de exploración y reedición de las relaciones asociativas en un espacio de solución geométrico. Es lo que se conoce como lógica paramétrica (Oxman, 2017).
El pensamiento de diseño paramétrico (PDP) y la definición de sus conceptos y principios en el diseño se pueden definir mediante la intersección de las tres perspectivas ilustradas en la figura 2 (Oxman, 2017):
- Modelos paramétricos: en referencia al esquema paramétrico en sí, englobando el modelo algorítmico y el código.
- Modelos cognitivos de conocimiento: que dependiendo del área de aplicación serán adaptados (diseño de producto, arquitectura, etc.).
- Modelos computacionales de procesos de diseño digital: sobre el esquema y flujo de información en procesos digitales.
El diseñador crea el código paramétrico para diseñar el objeto en cuestión (Oxman, 2017) (Barrios Hernández, 2006). Por tanto, el diseñador ya no toma decisiones sobre un objeto individual, sino que crea una matriz que abarca toda una población de diseños posibles (Oxman, Gu, 2015).
Esta lógica y razonamiento visual asociados al código paramétrico hacen que los conceptos y principios clave del PDT sean distintos a la lógica del diseño tradicional. Estos principios se pueden englobar en (Oxman, 2017):
- El esquema paramétrico como mecanismo de exploración cognitivo: la formulación del esquema paramétrico algorítmico es una capacidad cognitiva fundamental de la creatividad del diseñador paramétrico. Durante el proceso de diseño, el esquema paramétrico debe ser modificado y adaptado hasta su refinamiento.
- Exploración de variaciones paramétricas de las relaciones asociativas y estructurales: el poder de exploración para producir variantes dentro de un esquema paramétrico es una característica dominante del proceso de diseño paramétrico.
- Mecanismos de reedición algorítmica automática: la reedición del esquema paramétrico está ligada a la remodelación del modelo geométrico. Las herramientas paramétricas también proporcionan un mecanismo de exploración en el que se puede rastrear y reflexionar sobre el historial de la lógica de todas las modificaciones.
La modificación del modelo en diseño tradicional, generalmente, se logra mediante operaciones visuales de rediseño y remodelado del objeto de diseño. Mientras que los modelos tradicionales de pensamiento de diseño se refieren al elemento en sí, la reedición de diseño paramétrico se refiere al proceso de diseño representado por un conjunto de reglas algorítmicas definidas por el diseñador. La variabilidad paramétrica que típicamente incorpora el código hace de estos modelos una herramienta muy poderosa para la generación e innovación en diseño.
Diseño paramétrico como herramienta avanzada
La integración de softwares paramétricos ha supuesto grandes avances en el diseño y arquitectura y también ha influido en la manera de trabajar y pensar.
Creatividad y bocetos digitales
En casi todas las ramas del campo del diseño y el arte se comienza con el diseño de bocetos. El diseñador refina sus ideas mediante el razonamiento visual (Agirbas, 2020) (Iordanova, Tidafi et al., 2009). En este proceso, se realiza la conceptualización, modificación y refinamiento de forma iterativa y el diseñador desarrolla la idea de diseño.
Durante esta etapa conceptual del producto, los diseñadores exploran una gama amplia de soluciones en busca de conceptos atractivos y adecuados para las siguientes etapas de desarrollo (Alcaide-Marzal, Diego-Mas et al., 2020) (Martin-Erro, Domínguez Somonte et al., 2016-03). Un ciclo de diseño se nutre de la creatividad como principal mecanismo de propulsión y en este punto el diseñador no está completamente enfocado en el resultado final, sino que se centra más en el proceso y esto puede llevar a un punto muy diferente de donde se empezó a diseñar (Agirbas, 2020) (Lutters, Van Houten, Fred J. A. M et al., 2014). Por tanto, este no es un proceso lineal, sino un proceso continuo e iterativo de búsqueda (Barrios Hernández, 2006).

de botellas para toda la familia (Sun, Huang Aug
02, 2019).
La fijación, también conocida como el bloqueador de la creatividad, haceque el diseñador recurra a un espacio limitado de soluciones familiares cerrando la puerta hacia caminos inexplorados (Alcaide-Marzal, Diego-Mas et al., 2020) (Agirbas, 2020). Una forma tal vez más actual de realizar bocetos es mediante la creación de modelos digitales. Las herramientas avanzadas en diseño, como en el caso del diseño paramétrico, permiten explorar lo que se conoce como creatividad asistida por ordenador (Alcaide-Marzal, Diego-Mas et al., 2020). El diseño paramétrico puede constituir una forma de superar la fijación: el ordenador genera alternativas y conceptos donde el diseñador es capaz de explorar una gama más amplia de soluciones (Iordanova, Tidafi et al., 2009).
Los sistemas de DA más tradicionales requieren de datos estructurados y precisos, ya que, durante la fase de diseño conceptual, la información suele ser ambigua y no estructurada. Replicar el flujo creativo del boceto tradicional dentro del software DA puede ser difícil, además de ser una tarea lenta en muchas ocasiones. Por eso, las soluciones de diseño algorítmico constituyen un gran interés en esta área.
Más allá de lo ya mencionado, el diseño paramétrico permite explorar alternativas que el diseñador pueda dibujar, o incluso imaginar (Alcaide-Marzal, Diego-Mas et al., 2020) (Agirbas, 2020). El software pasa de ser una mera herramienta de representación, a “mediar” con el diseñador durante el proceso de diseño. El uso de este tipo de sistemas interactivos da como resultado una cooperación entre diseñador y computadora que reproduce fielmente la exploración en evolución a través de bocetos (Fig. 3).
Diversidad, rapidez y calidad en diseño
Las técnicas de diseño paramétrico ofrecen ventajas obvias para los procesos de ingeniería y fabricación (Schnabel, 2012). El diseño paramétrico permite una comprensión más profunda de los objetivos del diseño y guía a los diseñadores en sus decisiones en etapas tempranas del proceso de diseño. Además, es capaz de sugerir soluciones controlables y adaptables que reaccionan a las situaciones específicas propuestas por el diseñador.
2017).
Hernandez comenta es su trabajo: “El diseño paramétrico es el proceso de diseñar en un entorno donde las variaciones de diseño son fáciles, reemplazando así la singularidad con la multiplicidad en el proceso de diseño” (Barrios Hernandez, 2006). Las variaciones en el diseño son una parte fundamental del proceso de diseño en la búsqueda de soluciones a los problemas de diseño, y aseguran la mejora del diseño y calidad de producto. El control de los parámetros hace posible crear instancias de diseño particulares a partir de una gama potencialmente infinita de posibilidades (Oxman, 2017) (Stals, Jancart et al., 2020).
Hoy en día, la tecnología de modelado paramétrico se está adoptando en la gama de herramientas DA utilizadas por la industria, ya que proporciona una enorme flexibilidad para explorar alternativas de diseño viables. Las herramientas paramétricas facilitan y aceleran trabajos de diseño repetitivos o iterativos, haciendo del diseño paramétrico un método eficaz y eficiente para ahorrar tiempo y coste del diseño de productos.

geometría paramétrica (Yazdi, Nasiri, 2017).
Transformación vertical y generación de series
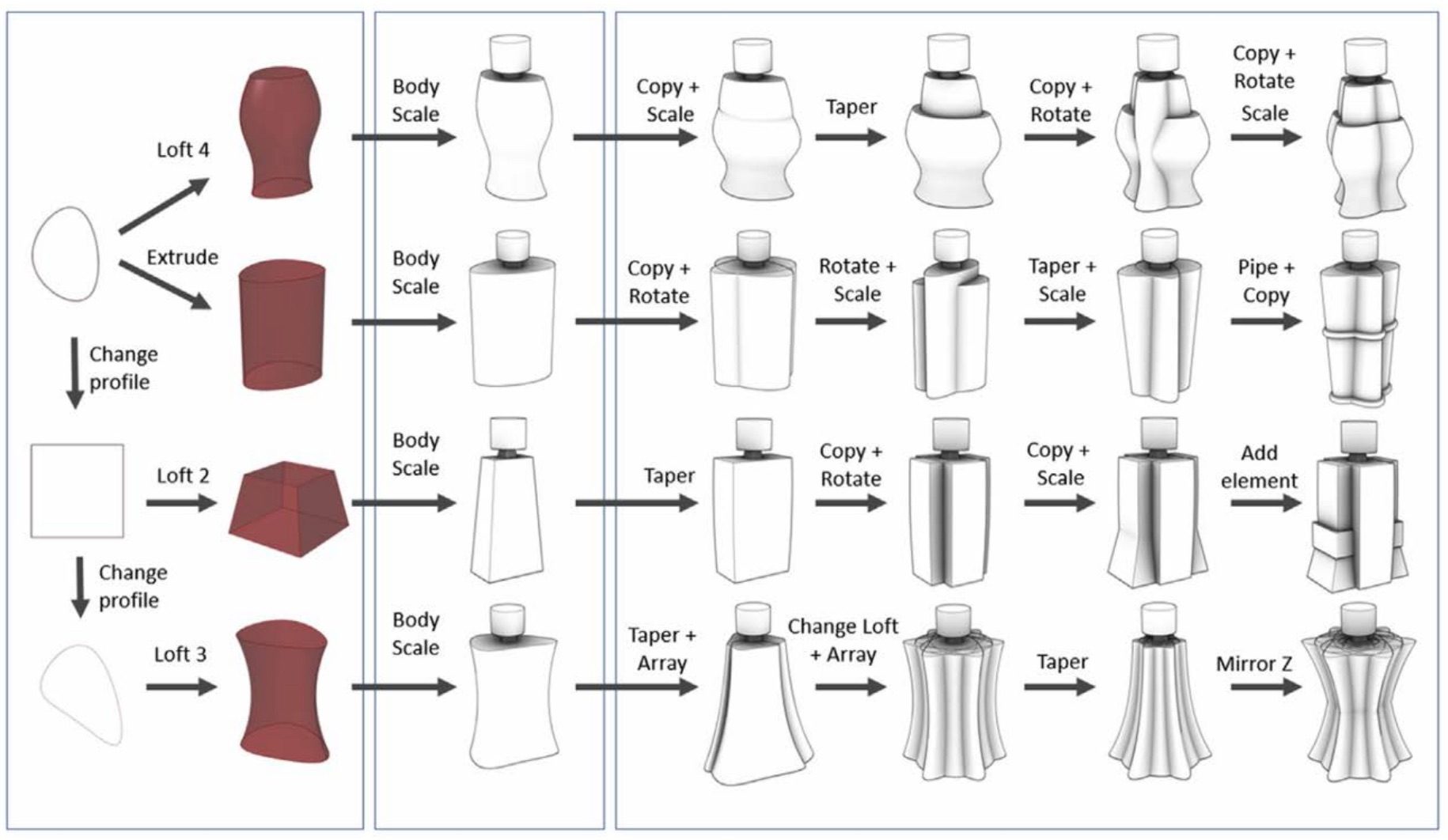
Una estrategia de exploración de diseño durante la fase de ideación es la de generar versiones de diseño basándose en una solución particular, también conocido como transformación vertical (Alcaide-Marzal, Diego-Mas et al., 2020). Supongamos que al diseñador le resulta atractiva una de las soluciones generadas y quiere generar variaciones de diseño a partir de esto. El potencial de herramientas paramétricas es que controlando la probabilidad de ocurrencia de cada parámetro se pueden crear gran cantidad de variantes aleatorias de diseño sobre el rasgo correspondiente.
Del mismo modo, esto permite crear series de diseños de manera eficaz y rápida (Sun, Huang Aug 02, 2019). La serialización de producto puede consistir en una estrategia comercial muy interesante, ya que permite mejorar la competitividad, establecer la imagen corporativa y expandir la influencia de marca en el usuario (Espinosa, Domínguez, 2017). Además, puede ahorrar el costo de diseño y el costo de producción y mejorar la capacidad de investigación y desarrollo. La planificación y el desarrollo de la serie de productos se debe realizar desdelos inicios de la fase de diseño, con lo que una herramienta de diseño acorde es importante (Espinosa Escudero, María del Mar, Domínguez Somonte, 2013).
Al diseñar una serie de productos, el diseñador no necesariamente debe comenzar desde cero; puede basarse en diseños existentes o rasgos de interés de la serie para las nuevas alternativas (Sun, Huang Aug 02, 2019). Los softwares paramétricos permiten aplicar este tipo de estrategia durante la etapa de diseño, acortando el tiempo y reduciendo la repetición trabajo. El pensamiento paramétrico y las herramientas de modelado proporcionan un gran potencial de aplicación en el diseño de serialización de todo tipo de productos (Fig. 4).

cantidad de material posible durante el moldeo por inyección (Hanson, 2019).
Personalización en diseño
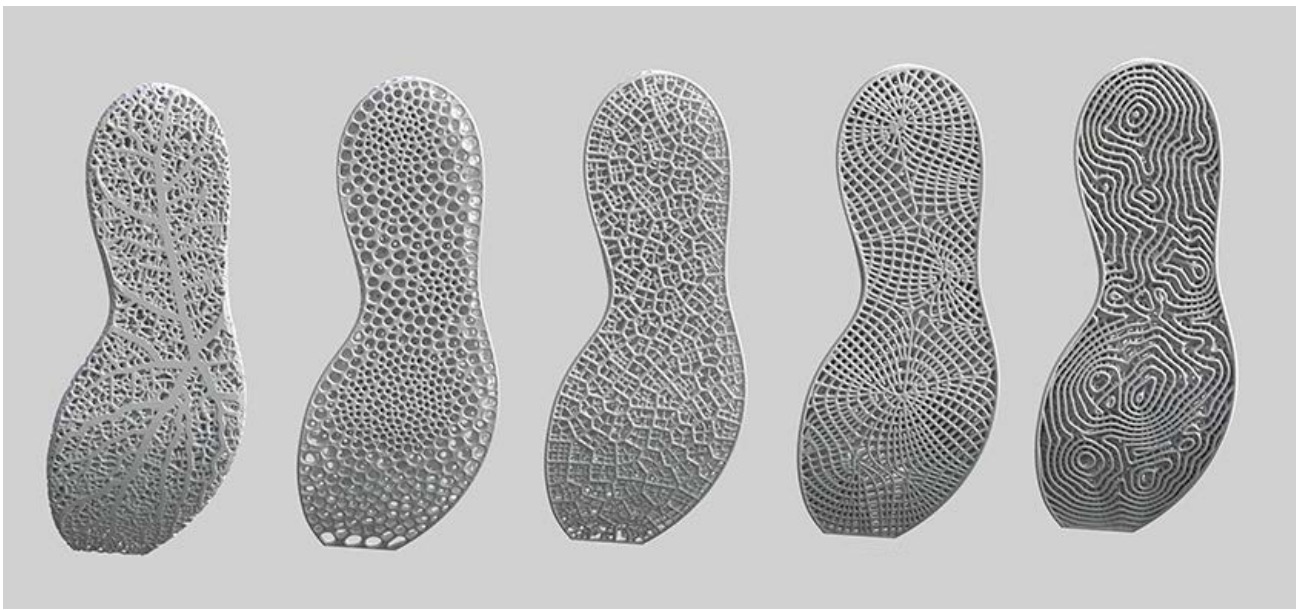
Desde la llegada del DA, la personalización de producto ha pasado de una producción artesanal a una realidad más extendida para la industria (Christodoulou, 2020). El diseño paramétrico ha permitido un nuevo nivel de personalización del producto al poder vincular los datos humanos directamente en el propio diseño, el proceso de ingeniería y la fabricación.
En particular, en el caso de la moda y el calzado, la tecnología 3D ha permitido grandes avances en varias direcciones del diseño de este tipo de productos. Por ejemplo, algunas empresas de calzado han intentado acercarse a las necesidades del consumidor utilizando tecnologías contemporáneas como la impresión 3D y nuevas estrategias de diseño. Los avances en diseño y fabricación han permitido producir componentes repetitivos no normalizados directamente a partir de datos digitales.
Una de las ventajas del diseño paramétrico y de la fabricación digital es que el fabricante puede tener un vínculo directo con las demandas anatómicas y estéticas del usuario, abriendo nuevas posibilidades para la personalización del producto. Parte de la industria de esta personalización masiva se trata de producir bienes con un alto grado de personalización con eficiencias casi industriales.
Aunque la revolución industrial ha traído consigo los beneficios de la producción en masa, el diseño paramétrico permite volver a la producción artesanal personalizada, gracias también a las ventajas de la fabricación digital (Fig. 5).
Integración de disciplinas en diseño
En el proceso de diseño convencional, el proyecto se coordina entre los profesionales involucrados, donde la idea de cambiar, editar y desarrollar el diseño es un proceso habitual e iterativo, hasta lograr el diseño óptimo y la mejor solución (Eltaweel, SU, 2017). Dependiendo de las diferentes disciplinas y de la magnitud del proyecto, este proceso iterativo puede suponer la integración de aspectos diversos durante la etapa de diseño. Tratar de integrar y coordinar estas relaciones puede resultar complicado, complejo, lento y arriesgado.
Los métodos paramétricos permiten una integración y coordinación mucho más flexible y adaptable a las distintas disciplinas involucradas en proyectos más complejos, facilitando la relación entre las disciplinas y aplicando las modificaciones sin problema. Estas modificaciones influirán en todas las disciplinas del proyecto sin necesidad de iterar todo el proceso del proyecto, ya que todos los parámetros, disciplinas y elementos están conectados paramétricamente (Fig. 6).
Diseño generativo
El concepto del diseño generativo está muy ligado a la existencia del diseño paramétrico (Khabazi, 2012) (Alcaide-Marzal, Diego-Mas et al., 2020). El diseño generativo es un proceso de diseño iterativo de optimización que involucra un programa que generará un número de soluciones de diseño limitado a ciertas restricciones. El diseño generativo va más allá del paradigma de diseño convencional de crear y después evaluar. Va directamente a crear alternativas que cumplan las especificaciones de diseño (García Menéndez, Domínguez et al., 2020).
Las herramientas de diseño generativo parten por delimitar los objetivos y las restricciones del objeto que se quiera diseñar y las expresan mediante parámetros. El proceso de diseño continúa con la generación y la evaluación de permutaciones ilimitadas de soluciones al problema planteado. Por tanto, se pueden distinguir tres elementos clave: a) un esquema paramétrico que defina el objetivo a diseñar, b) un medio para crear variaciones de diseño y c) un medio que evalúe y seleccione las variaciones creadas. Es en este primer punto del proceso donde el diseño paramétrico interviene.
Dependiendo del software generativo usado, las técnicas de diseño para crear variaciones son distintas; no obstante, todas parten de la necesidad de definir previamente la lógica de diseño mediante parámetros. Para encontrar una solución a un problema con varias variables, se necesita una función de criterios definidos para evaluar las soluciones paramétricas generadas por el programa (Khabazi, 2012). Se optimiza el diseño según estos criterios definidos por parámetros.
Desde un punto de vista de diseño de producto, también permite definir el método de fabricación desde un principio, traduciéndolo a una serie de parámetros a considerar durante la generación de los modelos (García Menéndez, Domínguez et al., 2020). Por tanto, el programa producirá diseños que solamente se puedan fabricar por el método seleccionado. Entre otros objetivos, el diseño generativo se puede emplear para optimización del material de uso o reducción del coste de fabricación y que desde un enfoque de diseño tradicional sería muy costoso debido a la dificultad de colaboración entre diseño, simulación y optimización. Es impensable la cantidad de expertos y tiempo que se requeriría para competir con la creación y optimización mediante herramientas generativas.
La mayoría de los softwares de diseño ofrecen una alternativa generativa, además de la herramienta paramétrica respectiva. Es el caso de las herramientas generativas como Galapagos en Rhino o GDE del software CATIA (Eltaweel, SU, 2017) (Geren, Akçal? et al., 2017); este último es capaz de generar automáticamente alternativas de objetos conceptuales en función de las especificaciones funcionales previamente planteadas. Una vez importadala geometría básica, y definidas las especificaciones de diseño y fabricación, el software genera la geometría optimizada. Después se generan variaciones del diseño con sus respectivas simulaciones para su evaluación, y el diseñador, por último, valida el modelo para después ser transformado en un modelo para fabricación. Las herramientas generativas permiten la integración de las fases de diseño, simulación y optimización.
Se podría observar el diseño generativo como el siguiente paso al diseño paramétrico, en el que, en este caso, el diseñador no selecciona las soluciones generadas por el software, sino que es el mismo programa el que encuentra el diseño óptimo en función de los criterios establecidos por el diseñador (Alcaide-Marzal, Diego-Mas et al., 2020). Gracias a los avances que se están produciendo actualmente tanto en softwares, materiales y fabricación, el diseño generativo supondrá el futuro del diseño y la fabricación (Fig. 7).
Limitaciones y retos de las herramientas paramétricas
Como cualquier otra herramienta de diseño digital, el diseñador debe dominar por completo el software paramétrico para obtener un grado de exploración de diseño profundo (Alcaide-Marzal, Diego-Mas et al., 2020). Además, teniendo en cuenta la necesidad de adaptación de la manera de pensar en diseño por parte del usuario, esto supone una mayor complejidad para la maestría del diseñador en las herramientas paramétricas (Oxman, 2017). Los softwares paramétricos actuales tienen amplias capacidades de modelado 3D paramétrico, pero también tienen ciertas limitaciones (Geren, Akçali et al., 2017):
• Las dimensiones de las piezas y los modelos de ensamblaje se pueden modificar fácilmente, pero para cambiar muchas dimensiones mediante un solo parámetro, se deben definir las relaciones en detalle por cálculos matemáticos y expresiones entre dimensiones.
• Los parámetros no numéricos que ofrecen algunos softwares paramétricos necesitan programación extra incorporada a los productos de software DA 3D.
• Es posible la incorporación de parámetros descritos fuera de la interfaz paramétrica (Microsoft-Excel o software DA 3d), pero el proceso se debe programar y puede resultar complicado.
• La exportación del modelo en 2D para planos debe de ser programada, en especial si es necesaria la incorporación de información extra para la fabricación.
• La flexibilidad de exploración en ensamblajes es limitada, ya que los softwares paramétricos actuales no permiten: a) configuraciones y alternativas de partes en un ensamblaje, b) variantes de topologías distintas y c) la gestión de piezas y características en diferentes ejes o planos.
Si bien el proceso de diseño paramétrico teóricamente tiene una adaptabilidad casi ilimitada del modelo, puede suponer limitaciones de diseño en modelos complejos (Stals, Jancart et al., 2020) (Schumacher, London, 2008). En algún momento, la complejidad del modelo puede hacer que sus posibilidades infinitas lleguen a su límite para que siga siendo comprensible. La complejidad creciente reduce así en cierto nivel la flexibilidad y adaptabilidad de la descripción algorítmica en sí.
Se podría decir que las herramientas paramétricas ofrecen unas alternativas de diseño ilimitadas, siempre y cuando el diseñador obtenga la maestría con estas herramientas, y los modelos objetivos no sean extremadamente complejos.
Por último, las restricciones de ingeniería (método de fabricación, maquinaria disponible, etc.) limitan tanto las propias alternativas del diseñador como los grados de libertad del modelo (Anderl, Mendgen, 1996). Las geometrías del modelo están íntimamente ligadas al método de fabricación, creando la necesidad de incluir estas restricciones al modelo. Los avances en nuevos métodos de fabricación, como la fabricación aditiva, están permitiendo ampliar estas restricciones de ingeniería y también creando otras. Además, estos métodos de fabricación muchas veces están limitados a soluciones que no se adaptan la fabricación en masa, limitando estos diseños a series, prototipos o incluso modelos íntegramente teóricos (García Menéndez, Domínguez et al., 2020). No obstante, los avances en nuevos métodos de fabricación están siendo rápidos y prometen un futuro con restricciones más flexibles de ingeniería para el diseño paramétrico.
Conclusiones
Desde la inclusión de las ecuaciones paramétricas en DA, la aplicación de esta estrategia en materia de diseño ha supuesto grandes avances en diseño de producto, mobiliario y moda. Estos avances no habrían sido posibles sin los métodos de fabricación contemporáneos (impresión 3D, máquinas CNC, etc.), así como herramientas digitales avanzadas.
Los softwares paramétricos son diversos, complejos y requieren de un cambio en la lógica del diseñador y el proceso del diseño. Las herramientas digitales pasan de ser un simple útil en el proceso de diseño a activamente diseñar los modelos de productos según el diseño de código creado por el diseñador.
El diseño paramétrico, por tanto, permite el ciclo de comunicación entre el diseñador y la herramienta digital. El modelo visual del diseño tradicional se reemplaza por la integración del código paramétrico y el modelo geométrico, y esta relación está respaldada por una interfaz visual para procesos de diseño, reedición e interpretación exploratorios.
Además de estimular la creatividad a través de la aleatoriedad, se ha demostrado que el diseño paramétrico proporciona a los diseñadores un espacio ilimitado de soluciones innovadoras y que abren la puerta hacia caminos inexplorados. Desde las primeras etapas del diseño, incrementa la creatividad de bocetos e ideas digitales, donde además tiene una influencia directa en la diversidad, rapidez y calidad de estos diseños. Permite explorar el concepto de marca y serialización de diseños de manera exponencial gracias a la transformación vertical. También ha facilitado la incorporación del concepto de personalización industrial al mercado, y ha permitido la integración de diferentes disciplinas en toda la fase de diseño. Por último, el diseño paramétrico ha sido el catalizador de la posibilidad del diseño generativo, en el que el diseñador no selecciona las soluciones generadas, sino que es el mismo software el que facilita el diseño óptimo.
Las limitaciones de las herramientas paramétricas como impulsoras de la creatividad principalmente residen en la necesidad del usuario de estar familiarizado con el software de DA. Esto implica la maestría en las herramientas paramétricas por parte del diseñador, así como una adaptación de la lógica de diseño del usuario. Cabe destacar que cada interfaz y la lógica que reside detrás de esta son variables dependiendo del software de uso, lo que complica aún más la transición del diseñador entre herramientas y limita sus ideas.
La evolución de las herramientas paramétricas con la inclusión de solucionadores variacionales supuso un avance en la facilidad de resolver los modelos, también aumentando su flexibilidad y permitiendo mayores alternativas para la creatividad del diseñador. No obstante, esto está limitado a la capacidad del diseñador de describir un modelo relativamente flexible, también teniendo en cuenta las restricciones de ingeniería (método de fabricación, etc.). La fabricación aditiva ha supuesto grandes avances en este sentido, pero las capacidades de producción en masa no son comparables a los métodos tradicionales de fabricación, y muchas veces los alejan de productos ordinarios de consumo final.
La llegada de las herramientas DA y la fabricación digital han supuesto un cambio drástico en la manera de pensar y diseñar, pero la capacidad de producción sigue limitando aún la creatividad del diseñador. Esbozar por código es una realidad hoy en día y es una herramienta muy útil para impulsar la innovación y creatividad del diseñador.
Referencias
AGIRBAS, A., 2020. A Teaching Methodology for Parametric Design: A Case Study with Parametric Bench, International Conference of the Iberoamerican Society of Digital Graphics 2020, Editora Blucher.
AISH, R. and HANNA, S., 2017. Comparative evaluation of parametric design systems for teaching design computation. Design studies, 52, pp. 144-172.
ALCAIDE-MARZAL, J., DIEGO-MAS, J.A. and ACOSTA-ZAZUETA, G., 2020. A 3D shape generative method for aesthetic product design. Design studies, 66, pp. 144-176.
ANDERL, R. and MENDGEN, R., 1996. Modelling with constraints: theoretical foundation and application. Computer aided design, 28(3), pp. 155-168.
BARRIOS HERNÁNDEZ, C.R., 2006. Thinking parametric design: introducing parametric Gaudi. Design studies, 27(3), pp. 309-324.
BHOOSHAN, S., 2017. Parametric design thinking: A case-study of practice-embedded architectural research. Design studies, 52, pp. 115-143.
CHRISTODOULOU, M., 2020. History of Parametric Design The History of Parametric Design and Its Applications in Footwear Design, ICDHS 2020, International Committee for Design History and Design Studies.
DAVIS, D., 2013. Modelled on software engineering: flexible parametric models in the practice of architecture, RMIT University.
ELTAWEEL, A. and SU, Y., 2017. Parametric design and daylighting: A literature review. Renewable & sustainable energy reviews, 73, pp. 1086-1103.
ESPINOSA ESCUDERO, MARÍA DEL MAR and DOMÍNGUEZ SOMONTE, M., 2013. Ingeniería Concurrente. 2 edn. Madrid: AIDA.
ESPINOSA, M.D.M. and DOMÍNGUEZ, I.A., 2017. Imagen en Ingeniería del Diseño. 1 ed. Madrid: AIDA.
GARCÍA MENÉNDEZ, L., DOMÍNGUEZ, M. and ESPINOSA, M.D.M., 2020. Diseño generativo: el estado del arte. Técnica Industrial, 327, pp. 44-49.
GEREN, N., AKÇALI, O.O. and BAYRAMO?LU, M., 2017. Parametric design of automotive ball joint based on variable design methodology using knowledge and feature-based computer assisted 3D modelling. Engineering applications of artificial intelligence, 66, pp. 87-103.
HANSON, E., April 9, 2019-last update, From Analog Ideas to Digital Dreams, Philippe Starck Designs the Future With AI. Available: https://redshift. autodesk.com/philippe-starck-designs/ [Feb 5, 2021].
IORDANOVA, I., TIDAFI, T., GUITÉ, M., DE PAOLI, G. and LACHAPELLE, J., 2009. Parametric Methods of Exploration and Creativity during Architectural Design. A case study in the design studio, CAADFutures, 2009 2009.
KHABAZI, Z., 2012. Generative Algorithms (using Grasshopper). Digital edn. Morphogenesism.
LUTTERS, E., VAN HOUTEN, FRED J. A. M, BERNARD, A., MERMOZ, E. and SCHUTTE, C.S.L., 2014. Tools and techniques for product design. CIRP Annals, 63(2), pp. 607-630.
MARTÍN-ERRO, A., DOMÍNGUEZ SOMONTE, M. and ESPINOSA ESCUDERO, MARÍA DEL MAR, 2016-03. The role of Sketching in Engineering Design and its presence on Engineering Education, 2016-03, IATED.
OXMAN, R., 2017. Thinking difference: Theories and models of parametric design thinking. Design studies, 52, pp. 4-39.
OXMAN, R., 2008. Digital architecture as a challenge for design pedagogy: theory, knowledge, models and medium. Design studies, 29(2), pp. 99-120.
OXMAN, R. and GU, N., 2015. Theories and models of parametric design thinking, eCAADe, Sep 16-18, 2015 2015, Education and Research in Computer Aided Architectural Design in Europe (eCAAe).
PALM, E. and MINANA-SORIANO, S., 2/11/, 2017- last update, Parametric Design and Footwear Industry. Available: https://parameterizing. wordpress.com/2017/11/02/parametric-designand-footwear-industry/ [26/01/, 2021].
SCHNABEL, M.A., 2012. Learning Parametric Designing. Industrial Engineering: Concepts, Methodologies, Tools, and Applications. IGI Global, pp. 197-210.
SCHUMACHER, P. and LONDON, 2008. Parametricism as Style – Parametricist Manifesto. London:
SHAH, J.J., 2001. Designing with Parametric CAD: Classification and comparison of construction techniques. In: F. KIMURA, ed, Geometric Modelling. Springer US, pp. 53-68.
STALS, A., JANCART, S. and ELSEN, C., 2020. Parametric modeling tools in small architectural offices: Towards an adapted design process model. Design studies, 72.
SUN, B. and HUANG, S., Aug 02, 2019. Realizing product serialization by Grasshopper parametric design, International Forum on Industrial Design, May 17-19, 2019 Aug 02, 2019, IOP Publishing.
YAZDI, M. and NASIRI, F., 2017-last update, GECO. Available: https://parametrichouse.com/geco/ [26/01/, 2021].


