Eficiencia del puente autoportante de Leonardo

Carla Torres Abad

Resumen
Introducción. Entre la multitud de diseños realizados por Leonardo da Vinci sobresalen los de puentes y este estudio analiza una estructura autoportante, sumamente liviana y fuerte, fácil de montar y desmontar, ya que se mantiene en pie gracias a su propio peso. El objetivo es determinar la máxima eficiencia que puede tener este puente. Material y métodos. Se procedió mediante construcción de modelos en papel. Se determinó cuál era la forma más eficiente que podían tener las barras realizando un ensayo de flexión en distintos modelos y eligiendo el más resistente. Resultados. Se registraron datos obtenidos de los diferentes ensayos de flexión. Se comparó el tipo de papel del que debía estar hecho el puente y después se rediseñó su estructura a partir de los datos obtenidos. Se propusieron tres modelos distintos con el software de simulación ANSYS Workbench Inc., se realizó un ensayo de flexión en cada uno de ellos y se estableció cuál fue el más eficiente. Se entendió eficiencia como el cociente entre el peso máximo soportado y el peso de la estructura. Conclusiones. La máxima eficiencia que alcanza este puente es 119,82 y esta viene determinada por los siguientes factores: características del papel, geometría de los elementos y diseño del puente. Además, la forma de la estructura, cómo distribuye las cargas y los esfuerzos a los que se ve sometido son, a nivel de eficiencia, dos conceptos dependientes uno del otro.

Palabras clave: Ingeniería de diseño; puente autoportante; Leonardo da Vinci; estructuras de apoyo recíproco; cálculo estructural; eficiencia de estructuras.

Abstract
Introduction. Among the multitude of designs made by Leonardo da Vinci, those of bridges stand out, and this study analyses a self-supporting structure, extremely light and strong, easy to assemble and disassemble, since it stands up thanks to its own weight. The objective is to determine the maximum efficiency that this bridge can have. Material and methods. We proceeded by building paper models. The most efficient form that the bars could have was determined by carrying out a flexure test on different models, and choosing the most resistant one. Results. Data obtained from the different bending tests were recorded. The type of paper the bridge should be made of was compared, and then its structure was redesigned based on the data obtained. Three different models were proposed, using the simulation software ANSYS Workbench Inc., and a flexion test was carried out on each of them, and it was established which was the most efficient, efficiency being understood as the quotient between the maximum weight supported and the weight of the structure. Conclusions. The maximum efficiency achieved by this bridge is 119.82 and this is determined by the following factors: paper characteristics, element geometry and bridge design. Furthermore, the shape of the structure, how it distributes loads, and the stresses to which it is subjected are, at the efficiency level, two concepts dependent on each other.

Keywords: Design engineering; self-supporting bridge; Leonardo da Vinci; reciprocal support structures; structural calculation; structure efficiency.

---

Recibido / received: 23/03/2020. Aceptado / accepted: 03/02/2021.
Facultad de Ciencias (Grado en Física). Universidad de Zaragoza. C/ Pedro Cerbuna, 12 – 50009 Zaragoza
E-mail: carlafusti@gmail.com.

---

Introducción
Justificación y problema planteado
La construcción con vigas cortas, entramadas, de madera es una de las más antiguas que se conocen, y ha constituido una solución específicamente utilizada para la edificación de puentes desde hace siglos (Tampone, 2005). A lo largo de la historia y, concretamente, a partir de la Edad Media, su evolución permitió la edificación de estructuras de apoyo recíproco.

Entre los manuscritos de Leonardo es posible identificar un grupo de diseños que podrían agruparse dentro de una misma categoría, la de estructuras de apoyo recíproco. La característica esencial de todos ellos es que utilizan vigas autoportantes. Lo interesante es que apuntan al interés preferente de Leonardo por hallar soluciones que permitieran salvar grandes luces con piezas cortas y manejables, dispuestas en mallas (Sánchez Sánchez, Escrig Pallarés y Rodríguez León, 2010), no solo destinadas a puentes, sino también a cúpulas y techumbres. Esto fue algo único en la vanguardia de su tiempo, que sí abordó estudios arquitectónicos sobre estructuras de madera (Palladio y Fausto Verancio). Y, además, pone de relieve el nivel teórico alcanzado por el Leonardo ingeniero, superior con respecto a Palladio, aunque menos investigado con respecto a este.

Si bien hay múltiples estudios sobre la faceta de Leonardo como ingeniero, e incluso sobre sus puentes (vid. Epígrafe 1.1.3), respecto a la estructura de puente autoportante no hay una bibliografía detallada sustancial (Scantamburlo et al., 2017). A pesar de que es un clásico de los diseños de puentes de palillos, con fines educativos principalmente, no es uno de los puentes más conocidos de Leonardo y, como resultado, la crítica y análisis sobre esta estructura es esporádica y no sistemática, sin continuidad como línea de investigación.

La utilización del papel tiene una justificación basada en la bibliografía especializada. A partir de los dibujos de Leonardo se han realizado numerosos estudios de estructuras modulares con pequeñas piezas y, más recientemente, se han utilizado para ejemplificar el desarrollo de los conceptos de reciprocidad o cabalgamiento (Sánchez Sánchez, Escrig Pallarés y Rodríguez León, 2010). Sin embargo, son muy pocas las aplicaciones prácticas que aprovechan sus conocimientos.

No se ha realizado hasta el momento un estudio y cálculo de la eficiencia de esta estructura de apoyo recíproco diseñada por Leonardo. Más allá de los resultados obtenidos, el proceso de investigación llevado a cabo permitirá esclarecer otros aspectos de este, como son los problemas que afectan a su montaje, la geometría de sus elementos, los esfuerzos o tensiones a los que se ven sometidos sus elementos (compresión, tracción, flexión, cortante y torsión) y la medición de la resistencia mecánica de estos elementos. Todo ello permitirá aportar nuevo conocimiento al ya existente sobre Leonardo desde el punto de vista de la ingeniería.

Antecedentes
En la Antigüedad romana se pueden destacar dos estructuras de apoyo recíproco fabricadas en madera que han sido objeto de estudio posterior, principalmente por los arquitectos renacentistas siglos más tarde (Funis, 2000; Tampone, 2005). Se trata del puente sobre el Rin construido por César y el levantado sobre el Danubio por Trajano. El primero fue erigido en el 53 a.C., en 10 días, según el relato del propio César (De bello Gallico, I.18), en un punto entre las localidades actuales de Urmitz y Weissenturm, en Alemania. La solución adoptada, básicamente pensada frente al problema del empuje de las aguas del río, consistió en descansar la superestructura sobre soportes caballetes con estructura de dos vigas gruesas (diámetro de 45 cm), hechas en madera robusta, que adoptaban la forma de escaleras opuestas a la corriente del río. El puente sobre el Danubio fue diseñado por Apolodoro de Damasco y levantado entre el 103 y el 105 d.C. Estaba formado por sólidos pilares cuadrangulares de mampostería sobre los que descansaban 20 arcos construidos con vigas de madera entrelazadas. Se puede contemplar en uno de los bajorrelieves de la Columna Trajana, en la escena XCIX.

El principal antecedente directo del puente autoportante diseñado por Leonardo se puede encontrar en el conocido como Puente del Arco Iris, edificado en la localidad de Jinze, China, durante la época de la dinastía Song (960-1280) y del que únicamente se dispone de noticias por una serie de pinturas obra del artista Zhang Zeduan (El festival Qingming junto al río, del siglo XII) y por un experimento reciente. Se han llegado a identificar 11 puentes construidos con estructura de vigas de madera en las provincias de Zhejiang y de Fujian pertenecientes al mismo periodo (Yang, Chen y Gao, 2007; Yang et al., 2012). El propio Leonardo pudo tener conocimiento de esta obra y servirle de inspiración para su puente autoportante, debido a la enorme similitud de ambos (Sánchez Sánchez, Escrig Pallarés y Rodríguez León, 2010).

En 1999 el programa NOVA, del canal de televisión público PBS de Estados Unidos, organizó un equipo de ingenieros que, bajo la supervisión del profesor Tang Huancheng, estudioso de esta edificación, reconstruyó el puente arco iris utilizando técnicas antiguas (Altabba, 1999).

En el contexto histórico de Leonardo los arquitectos renacentistas como Palladio y Fausto Verancio abordaron masivamente, a nivel teórico y aplicado a casos de estudio concretos, la construcción de puentes de madera (Tampone, 2005).

Leonardo fue un paso más allá. Llegó a diseñar tres tipos de puente que pueden apreciarse entre sus manuscritos recogidos en el Código Atlántico (Ceraldi y Russo Ermolli, 2004). Aunque su diseño de puente autoportante estaba motivado por fines militares, en realidad parece que respondía a toda una categoría de estructuras proyectadas que podrían englobarse, en palabras del propio Leonardo, «che fa la volta per il tutto» (hoja 899 del Código Atlántico, ex. 328; Marinoni, 2000), es decir, de apoyo recíproco. Tienen en común todos ellos que son edificados con vigas autoportantes y que reflejaban la preocupación preferente de Leonardo por hallar soluciones para salvar grandes luces con piezas cortas y manejables, dispuestas en mallas (Sánchez Sánchez, Escrig Pallarés y Rodríguez León, 2010).

La originalidad de estos diseños al mismo tiempo evidencia el conocimiento por Leonardo de todo el saber técnico acumulado en los siglos medievales y de época antigua (Pizzigoni, 2010; Pisano, 2013). Con él, la importancia de las estructuras de apoyo recíproco, especialmente destinadas a la construcción de cúpulas o techumbres, pasa de la mera conjetura experimental a ser considerada una solución tecnológica, como testimonia el hecho de ser incluida en I Sette libri dell’architettura, tratado de arquitectura escrito por Sebastiano Serlio hacia 1537.

El puente autoportante de Leonardo da Vinci, diseñado en el año 1482, localizado en las páginas 69ar y 71v del Códice Atlántico, se caracteriza por ser sumamente liviano y fuerte, fácil de montar y desmontar, ya que sin necesidad de ninguna sujeción (clavos, tornillos, cuerdas u otro medio) se mantiene en pie gracias a su propio peso. Además de esto, su forma arqueada permite distribuir las fuerzas de carga al entrelazar las vigas longitudinales con las horizontales (Ceraldi y Russo Ermolli, 2004; Gancedo, 2011). En realidad, es reproducido por Leonardo en varios bocetos distintos procedentes de diferentes páginas del Código y, aunque difieren en la altura del arco, algo determinante, responden todos ellos a la misma configuración geométrica.

La finalidad inicial de este puente era ayudar tanto en la huida de las tropas como en la persecución de soldados enemigos. En la época en la que Leonardo vivió Italia permanecía en continuo estado de guerra, tanto interna como externa. Por ello, aquellos que aspiraban a los puestos de poder necesitaban disponer del mejor ejército y de los mejores ingenieros militares. Y esa es la razón de la carta de Leonardo a Ludovico El Moro fechada en 1482, en la que describe toda una serie de armas y gran cantidad de sus inventos militares más creativos, entre ellos su puente autoportante (Pedretti, 1978).

La importancia de los puentes de madera diseñados por Leonardo y su trascendencia para la técnica posterior es que le sirvieron para configurar el teorema sobre la propiedad de la no deformabilidad que posee la malla triangular, a pesar de que únicamente pudo demostrarlo mediante la geometría, único criterio de verificación disponible en su época (Tampone, 2005; Pisano, 2013; Cerveró Meliá, Ferrer Gisbert, y Capuz-Rizo, 2016). Las estructuras reticulares realizadas hasta entonces eran diseñadas en función únicamente de la intuición (Russo Ermolli y Mormone, 1996). La aportación de Leonardo fue hallar una justificación y racionalización concretas. La solución que propone el puente autoportante parece basarse en la preocupación por evitar la fragmentación excesiva de los elementos de madera causada por deformaciones indeseadas de estructura que resultan en desgaste articular (Pedretti, 1978; Tampone, 2005; Hutchings, 2016).

Estado de la cuestión
La construcción de puentes en madera a lo largo de la historia ha sido objeto de estudio importante en la literatura especializada desde hace décadas. Sobre la construcción de puentes en arco con vigas de madera y específicamente en el contexto de la arquitectura renacentista destacan los trabajos de Tampone (2000, 2001, 2005). En general, y dentro de este tema concreto de los puentes de madera, Palladio ha recibido más atención por parte de la investigación que Leonardo (Azzi Visentini, 1980; Russo Ermolli y Mormone, 1996; Funis, 2000; Heyman, 2000; Tampone, 2000). Al primero se le reconoce su innovación a nivel de materiales y de la estructura, y también por la aplicación en diferentes obras; pero a Leonardo se le atribuye, como se ha visto, la autoría teórica del diseño.

El interés por la faceta de ingeniero de Leonardo tuvo un punto de inflexión a partir de la década de 1960 (Hutchings, 2016), y fue como consecuencia, principalmente, de la recuperación de los códices de Madrid y de las publicaciones de Reti (1967, 1968a y 1968b). Hasta entonces, la investigación sobre Leonardo se había centrado mayoritariamente en su obra artística y científica, además de sobre su biografía (White, 2002; Kemp, 2006); salvo excepciones puntuales, como los estudios de Duhem a comienzos del siglo XX (Études sur Léonard de Vinci, 1906- 1913). Fue pionero, a este respecto, el enfoque adoptado por Usher en una temprana obra de 1929 en la que proponía investigar la obra de Leonardo dentro de cada campo de conocimiento, en este caso la ingeniería, en función de las consideraciones epistemológicas y técnicas de cada disciplina.

A partir de los dibujos de Leonardo se han realizado numerosos estudios de estructuras modulares (con pequeñas piezas) y más recientemente se han utilizado para ejemplificar el desarrollo de los conceptos de reciprocidad o cabalgamiento; sin embargo, son muy pocas las aplicaciones prácticas que aprovechan sus conocimientos (Sánchez Sánchez, Escrig Pallarés y Rodríguez León, 2010). Las contribuciones más relevantes a este respecto proceden, precisamente, de este grupo de trabajo de la Universidad de Sevilla, desde la década de 1990, integrado por J. Sánchez-Sánchez, F. Escrig Pallarés, M. T. Rodríguez León y Pérez Valcárcel, entre otros (Pérez Valcárcel y Escrig Pallarés, 1994; Sánchez Sánchez, Escrig Pallarés y Rodríguez León, 2014; Freire Tellado et al., 2019; Pérez Valcárcel, Frei Tellado y Muñoz Vidal, 2019).

Por el contrario, sobre la obra, vida e influencia de Leonardo da Vinci en la ciencia sí que se dispone de un corpus de bibliografía especializada, y se pueden destacar a este respecto las obras de Keele, Richter y su hija, Kemps, Foley y Soedel.

Métodos

El diseño experimental aplicado a esta investigación se desarrolló en una serie de fases que se describen a continuación: A. Estudio de la forma de las barras para el montaje. Para determinar la geometría de las piezas que forman el puente se barajaron las siguientes opciones:

• Con papel reciclado, hecho a mano, de forma que pudieran quedar macizo.

• Doblar los folios de papel repetidamente, de manera que la sección de las barras tendría forma de óvalo.

• Enrollándolos desde su ancho, de forma que la sección circular resultante (diámetro de la base de la barra) fuese lo más pequeña posible.

• Recortando en el folio un cuadrado y, después, doblándolo siguiendo su diagonal.

A.1. Ensayos de flexión en los tipos de barras propuestas. El ensayo de flexión consiste en lo siguiente. Se colocan dos soportes en los extremos de las probetas de papel, con el fin de que queden lo más sujetas posible, y se aplica una fuerza desde el centro de las mismas hasta conseguir romperlas (Fig. 1). Las fuerzas aplicadas se han de medir en Newton (N) mediante un dinamómetro. O, en su defecto, aplicando un peso desde el centro de la barra e ir aumentándolo paulatinamente hasta que la probeta se rompa, y después convertir dicho peso en Newton, es decir, multiplicando el resultado por 9,8, la aceleración de la gravedad en la Tierra. La barra seleccionada será aquella capaz de soportar la carga máxima mayor.

A.2. Selección de la probeta a utilizar según su eficiencia. Para determinar cuál de ellas es la más eficiente, primero se han de construir tres probetas para cada uno de los modelos, utilizando el mismo tipo de papel, de gramaje 80 g/m², y deben tener todas la misma longitud, 14 cm. Posteriormente, se realizará un ensayo de flexión para cada una de las probetas.

B. Determinación del papel a utilizar. Se tuvieron en cuenta una serie de características técnicas que tiene este material: gramaje, higroscopicidad, anisotropía y falta de homogeneidad.

B.1. Construcción de puentes con barras de papel de distintos gramajes.

B.2. Ensayos de flexión en los distintos puentes.

B.3. Determinación del más eficiente. Para ello, se tuvieron en cuenta las posibles variables de peso, luz, gramaje, longitud, diámetro y forma de las barras.

C. Rediseño del puente autoportante.

C.1. Cálculo estructural del puente original. Mediante los programas de Autodesk Fusion 360 y ANSYS Workbench Inc., con el fin de identificar los esfuerzos principales a los que se ve sometido y la manera en la que las cargas se distribuyen, para así optimizarlo, rediseñando su geometría y aumentando su eficiencia. Con el fin de simplificar este estudio, se supuso que los apoyos del puente son fijos, por lo que el rozamiento de estos contra el suelo sobre el que se apoyan no se tuvo en cuenta; la estructura es rígida, lo que significa que no sufre ningún tipo de deformación plástica debido a cargas inferiores de la necesaria para romperlo. Además, el ambiente en el que se encuentra es el ideal, por lo que se desestimaron los estudios referentes al medio y al análisis de los factores de seguridad, como los factores sísmicos y por viento.

C.2. A partir de los resultados, se optimiza el puente para aumentar su eficiencia. Se rediseña la geometría del puente, construyendo varios puentes distintos y observando, nuevamente, mediante un ensayo de flexión en cada uno de ellos, la carga máxima soportada.

D. Construcción del nuevo puente y determinación de su eficiencia. La eficiencia más alta hallada en el paso anterior C.2. se estimará que sea la mayor que pueda tener esta estructura autoportante, por lo que el puente que la obtenga ha de ser, en consecuencia, la versión más eficiente del diseño.

Resultados

Estudio de la geometría de las barras
En el estudio de la geometría de las piezas, se analizaron cada uno de los modelos propuestos anteriormente:

1. Barras construidas a partir de papel reciclado casero, haciendo manualmente la pulpa con papel desmenuzado en agua y licuado en una batidora. Al construir el papel de forma casera se le puede dar la forma que se desee, de manera que las barras creadas a partir de este método serían macizas.

2. Doblando el folio de papel repetidamente, obteniendo barras con sección ovalada.

3. Enrollándolo desde su lado menor, obteniendo barras con la sección más pequeña posible.

4. Recortando en el papel un cuadrado de 210 × 210 mm y enrollarlo siguiendo su diagonal.

Las dos primeras opciones se descartaron tras un examen preliminar. Esto es debido a que, por una parte, las fibras del papel reciclado casero no quedan bien distribuidas y, por tanto, las barras serían poco resistentes, y, por otra parte, las de sección ovalada, debido a su forma, no tendrían una resistencia homogénea (desde su diagonal mayor soportarían una carga más alta que desde su diagonal menor) y la estructura hecha con ellas no sería estable.

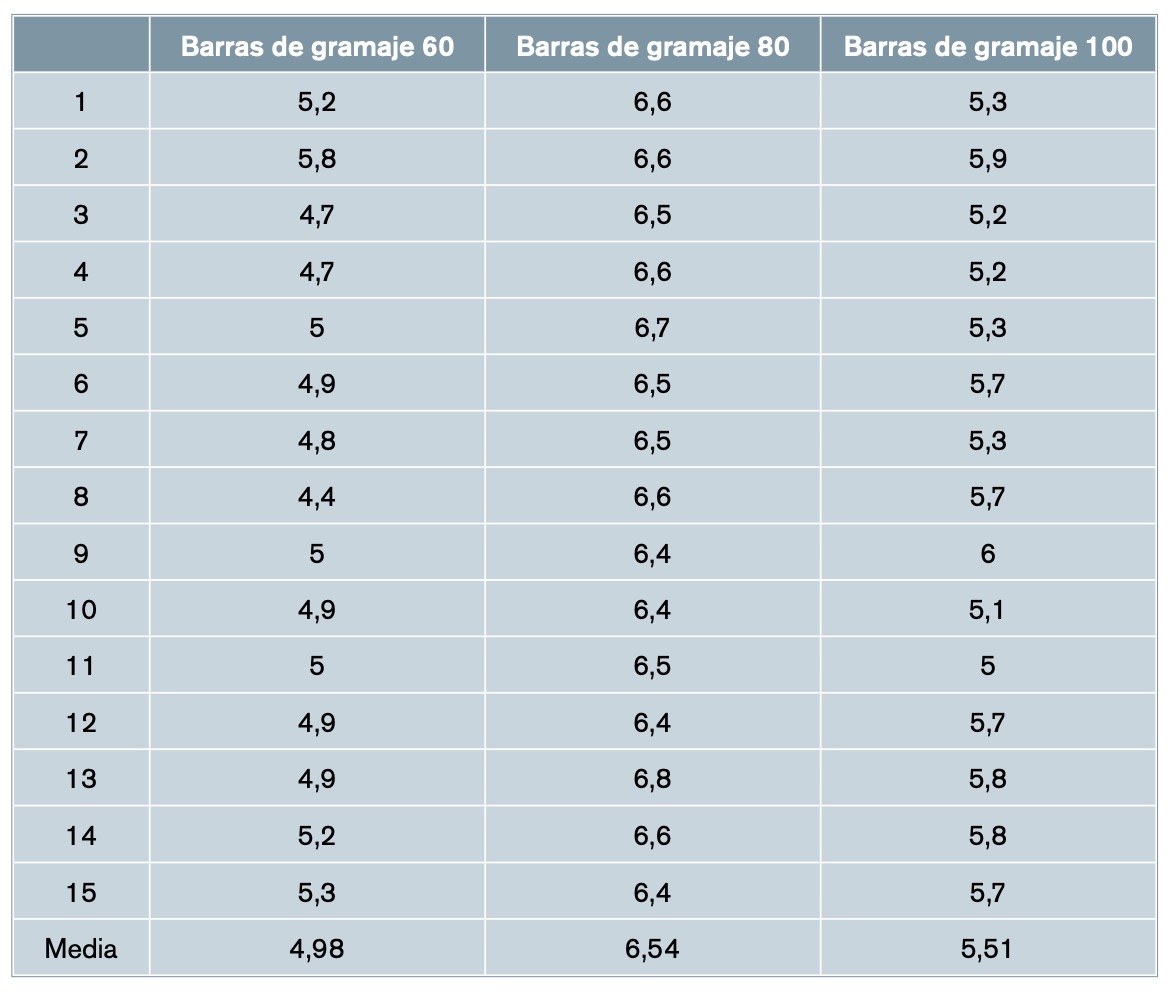
Finalmente, solo se realizaron ensayos de flexión en los dos últimos modelos. Se construyeron tres probetas de cada uno, con papel de 80 g/m², como ya se ha explicado anteriormente, y se obtuvieron los resultados mostrados en la tabla 1.

Como se puede comprobar, las barras del modelo 2 propuesto, que tienen una sección menor, soportan una carga máxima mayor que las del modelo 1. Por tanto, se constató que el modelo 2 es más eficiente y, por ende, es el que se utilizó en la construcción del puente.

Determinación del papel a utilizar
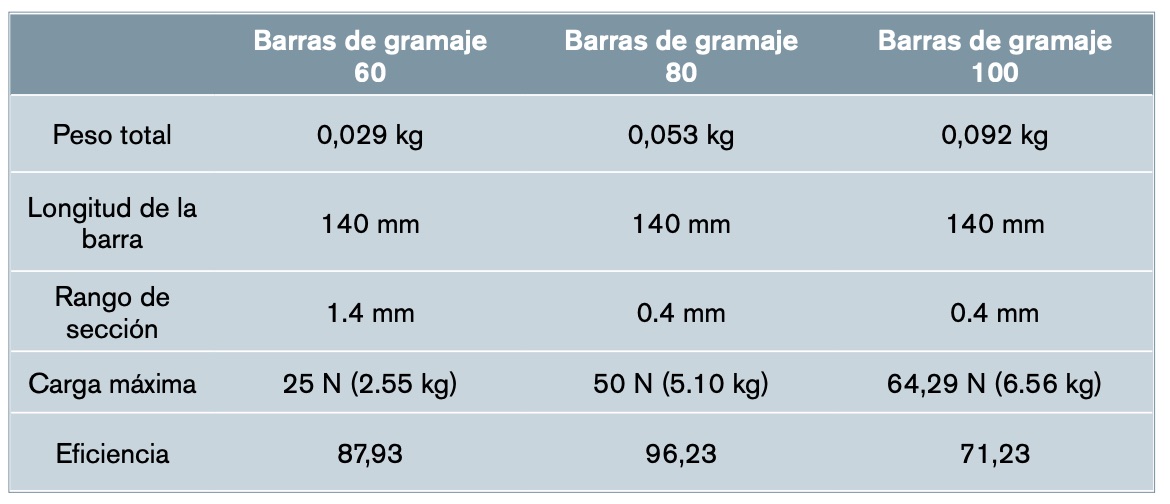
A partir del modelo de probeta seleccionado, se ha de determinar el tipo de papel con el cual se va a confeccionar el puente final. Para ello, como ya se ha explicado, se construyeron tres puentes con la misma luz y altura, de gramajes de 60 g/m², 80 y 100, y se realizó para cada uno de ellos un ensayo de flexión (Tablas 2 y 3).

Como se puede comprobar en los datos presentados, a pesar de que el tercer modelo soporte la carga máxima más alta, es el puente de menor eficiencia, ya que su peso es demasiado elevado. Por tanto, el puente más eficiente de todos sería el modelo 2, el de papel de gramaje de 80 g/m². Además de esto último, se puede observar que las probetas de este último puente son más homogéneas que las del resto, debido a que el rango de las secciones de este (la diferencia entre la probeta demayor sección y la de menor) es un número menor al de los demás puentes. Esto se debe esencialmente al gramaje de papel. Construir las piezas con el papel de periódico, de 60 g/m², al tener una rigidez tan baja, fue más difícil; al igual que pasa con el último puente, que, al tener una mayor rigidez, el papel se doblaba continuamente al intentar enrollarlo. Por tanto, se deduce que el resultado más fiable es el del segundo puente.

Análisis aparte merece la carga máxima registrada en el segundo puente al realizar este ensayo de flexión. Se puede observar que la fuerza necesaria para romperlo es ligeramente menor que la registrada en el estudio anterior de la geometría de las barras, en el que se utilizó el mismo tipo de papel.

Estos ensayos se realizaron en estaciones distintas del año, con lo cual la temperatura ambiente y la humedad del aire en el taller del que se disponía fueron distintas en los dos casos. En consecuencia, se estima que, debido a la higroscopicidad propia del papel, sus propiedades mecánicas pudieron verse afectadas por estas condiciones.

Por esta misma razón, se decidió dar una mayor rigidez a los apoyos uniendo entre sí las piezas del puente con silicona líquida, a pesar de que se puede construir sin necesidad de ello. Esto comportó que, en suma, la carga máxima soportada por esta estructura fuese mayor, por lo que, de no haberlo hecho, la cifra registrada para el puente de barras de papel de gramaje 80 hubiese sido menor.

Rediseño del puente, construcción y determinación de su máxima eficiencia
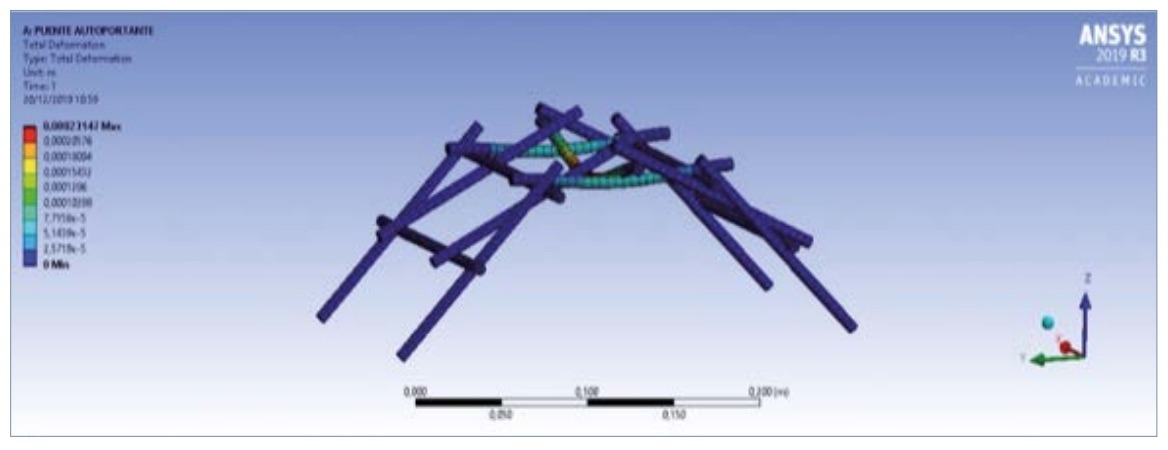
A partir de las medidas y proporciones del puente elegido en el apartado anterior, se realizó el cálculo estructural del puente inicial. Realizando un diseño en AutoDesk (Fig. 2) y, posteriormente, mediante el programa de ANSYS Workbench (Fig. 3), se estudiaron las deformaciones plásticas que sufre dicho puente debido a la carga máxima prevista, mediante lo cual se pudieron analizar los esfuerzos sufridos por los elementos de la estructura y la distribución de las cargas.

Sin embargo, el material que se tuvo que seleccionar en el programa para realizar dicho cálculo fue el bambú. Esto se debe a dos razones específicas. Dentro del software de Workbench existe una biblioteca con una amplia cantidad de materiales de construcción. Sin embargo, el papel no se encontraba entre ellos. Se podía incluir dentro de los archivos de la aplicación como un nuevo material, pero para llevar a cabo esto último, es necesario introducir unas características básicas sin las cuales el software no puede operar. En el caso del papel, estas propiedades no están registradas, ya que no es un material que se use en construcción de forma comercial, además de que las compañías que lo fabrican son reacias a mostrar esta clase de datos, ya que puede ser desventajoso a nivel empresarial. Por tanto, se eligió el material más semejante a él, el bambú, cambiando su densidad e introduciendo la del papel trabajado, 80 g/m².

Como se puede apreciar, la zona central, en especial la barra meridional, es la que mayor esfuerzo sufre (de flexión), como la mayoría de las tensiones presentes en la estructura. También están presentes los esfuerzos de compresión en las barras laterales y de cizalladura en las uniones entre barras. Sin embargo, al ser estas tan leves, se pueden desestimar dentro del análisis. Por tanto, las barras centrales han de tener un grosor mayor que las laterales.

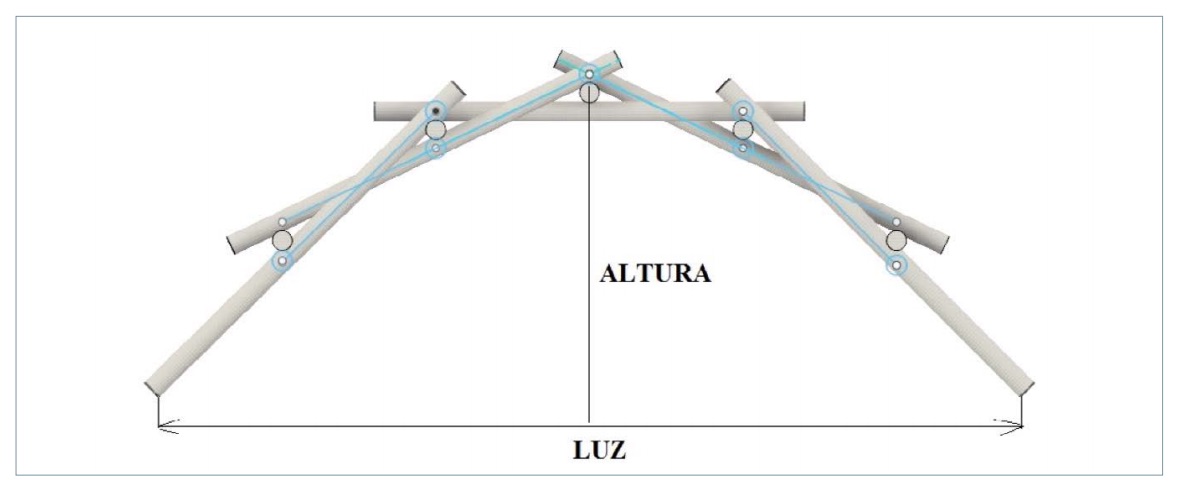
Además, debido a la curvatura del puente o, dicho de otro modo, al ángulo que forman las barras inclinadas con respecto a la superficie de sujeción, las cargas se distribuyen de tal manera que, al descomponerlas, la componente en el eje X es mayor que la del eje Y. Por tanto, el puente tiende a abrirse, lo que provoca inestabilidad en la estructura. Se constata entonces que a mayor ángulo de las barras con respecto al suelo, es decir, cuanto más verticales sean las cargas, mayor es la estabilidad. Como consecuencia, el peso máximo soportado por la estructura será mayor.

A nivel geométrico, esto se traduce en un puente con mayor altura y menor luz que el inicial. Para que la estructura analizada tenga las anteriores características, la parte de la barra que ha de sobresalir a la hora de construirlo ha de ser mayor. En el diseño inicial, esta medida se estimó que fuese de 1 cm; en el final, esta longitud es de 3, ya que, eligiendo una distancia menor, el cambio apenas sería perceptible, y eligiendo una mayor, la inclinación de las barras sería demasiado alta, por lo que quedarían casi perpendiculares con respecto al suelo.

Teniendo en cuenta lo dicho anteriormente, la geometría propuesta y que el peso del puente optimizado ha de ser igual al peso del puente seleccionado en el apartado anterior, se propusieron los siguientes tres modelos:

En el primer modelo, únicamente se aumentó la sección de la pieza central y su momento de inercia. Para ello, se debió aumentar su masa, disminuyendo consigo la masa de las cuatro barras laterales más inclinadas. Al ser esta pieza la que más tensión sufre, se determinó que fuese la modificada en los tres modelos.

Sin embargo, en el segundo modelo, se aumentó la barra central y las dos barras laterales, ya que, al ser entonces la componente en el eje Y la mayor, era posible que estas sufrieran un nuevo esfuerzo de compresión no previsto, lo que podría alterar la eficiencia de la estructura. Pero, al aumentar por igual la masa de estas tres barras, se debió disminuir, a su vez, la masa de las cuatro barras con el menor grado de inclinación.

Por último, en el tercer modelo se aumentó la masa de las tres barras centrales, por lo que disminuyó consigo la de las cuatro barras menos inclinadas.

La relación existente entre las barras de peso aumentado y las de peso disminuido es la siguiente. Dado que el resto de piezas del puente siguen conservando su masa inicial, el peso que han de reunir las barras modificadas ha de ser igual al peso que debieran tener el mismo número de barras de peso no modificado. Por tanto, se estimó que el total de barras mayores tendría que ser equivalente a la mitad del peso total de todas las piezas modificadas. Por ejemplo, suponiendo que se ha aumentado la masa de una barra y se ha disminuido la de cuatro y que el peso total de todas ellas juntas debiera ser 30 gramos, la barra mayor pesaría 15 gramos y las cuatro barras menores juntas los otros 15.

Para aumentar la masa de las barras simplemente se enrolló alrededor de una probeta normal papel de las mismas características hasta que estas adquiriesen la masa ideal. Para disminuir la masa, a la hora de formar las barras, no se enrollaron hasta el final de papel, sino hasta el punto donde este tuviera la masa buscada.

Se aplicó, nuevamente, un ensayo de flexión para cada uno de los tres puentes, y se obtuvieron los resultados mostrados en la tabla 4.

Como se puede comprobar, el modelo más eficiente es el modelo 3. En consecuencia, se determina que esta es, a nivel estructural, la mejor versión del diseño del puente autoportante de Leonardo da Vinci, y el valor de eficiencia registrado es la máxima eficiencia de dicho puente.

El fallo principal del primer modelo fueron las dos barras laterales, cuyas bases actúan como los apoyos del puente. Al modificar la geometría de la estructura de forma que las cargas fuesen más verticales, estas barras sufrían un leve esfuerzo de compresión. En consecuencia, al cambiar su masa, no pudieron soportar tal tensión y se rompieron antes incluso que las barras centrales. Esto se traduce en una eficiencia menor de la esperada previamente.

Comparando los modelos 2 y 3, se verifica que, efectivamente, los esfuerzos más relevantes, a pesar de modificar el diseño del puente, son siempre los esfuerzos de flexión centrales. Esta es la razón por la cual el último modelo es el más eficiente de todos, ya que su masa está distribuida de tal forma que los esfuerzos se compensen.

Conclusiones
El puente autoportante de Leonardo da Vinci es, como ya se explicó, una estructura muy práctica, ya que se puede montar y desmontar con facilidad, además de poder soportar una gran carga, lo que lo hace muy eficiente, como se ha demostrado anteriormente.

Sin embargo, el diseño inicial de este puente contaba con una ligera desventaja: la zona central. Esta, según los datos obtenidos, es la más afectada por la carga aplicada a la estructura, lo que comportaba que sufriera un esfuerzo de flexión considerablemente elevado.

Por tanto, el peso del puente no estaba bien distribuido, ya que estaba repartido homogéneamente. Todos sus elementos contaban con las mismas características, cuando, para vencer dicha tensión, la masa se había de concentrar en la zona más débil, en particular la barra meridional y las dos perpendiculares a ella. Aparte de eso, el puente ha de tener una mayor altura y menor luz, es decir, sus barras inclinadas debían de forma al mayor ángulo posible con respecto a la superficie de sujeción para que la componente de la carga en el eje Y fuese mayor que la del X, lo que deriva en una mayor estabilidad estructural. Sin embargo, esta modificación comportaba que el esfuerzo de compresión sufrido por las barras laterales era mayor, por lo que la masa de dichas barras no se puede modificar. A pesar de ello, se demostró que el esfuerzo principal seguía siendo el de flexión.

De esta forma, se deduce que el puente autoportante de Leonardo da Vinci, a pesar de estar diseñado de una forma bastante ingeniosa, para ser efectivo y práctico, debe tener una altura muy elevada, lo que hace inviable su uso en la vida real. Por eso no se llegó a utilizar nunca, como muchos otros de sus inventos. A pesar de ello, todos sus diseños e investigaciones influyeron en gran medida sobre otros proyectos de arquitectura e ingeniería posteriores, además de en otras disciplinas, como la docencia, con las ya mencionadas estructuras de palillos y papel y los nuevos concursos de puentes.

En cuanto al material utilizado a lo largo de este trabajo de investigación, el papel, se puede constatar que se trata de un material muy versátil, lo que permitió poder manejarlo con facilidad, en especial para la geometría de las piezas analizadas en este trabajo, barras tubulares, ya que el papel se puede enrollar con facilidad. Otros materiales, como la madera, requieren de un tratado industrial específico para que la pieza a diseñar tenga las medidas y características deseadas. Por tanto, estas propiedades hacen del papel un material ideal para el diseño de estructuras a nivel educativo.

En añadido, se determinó que, de todos los tipos de papeles, el de mayor eficiencia (relación masa del cuerpo con la carga máxima soportada por él), es el de gramaje 80 g/m².

Teniendo en cuenta lo dicho, se deduce, por tanto, que la hipótesis propuesta, aunque es correcta, está incompleta. La eficiencia del puente autoportante de Leonardo da Vinci hecho de papel no solo viene determinado por el gramaje del mismo, la geometría de sus elementos y el diseño del mismo puente, sino también por la forma en la que el diseño afecta a la dirección de las cargas y, consigo, el aumento o disminución de ciertos tipos de esfuerzos (como en el caso de las barras laterales), además de la forma en la que la masa de la estructura se distribuye para vencer dichas fuerzas. El diseño de la estructura y los esfuerzos del mismo, en cuanto a eficiencia, son dos conceptos íntimamente ligados, ya que uno depende del otro.

Agradecimientos
Ambos autores quieren agradecer los comentarios y mejoras hechas a la memoria original de esta investigación por parte de Juan Pérez Valcárcel, catedrático del Departamento de Construcciones y Estructuras en la Universidade da Coruña. A la autora le gustaría destacar el apoyo recibido por el instituto de educación secundaria I.E.S. Valle del Ebro, en especial a los profesores del Departamento de Tecnología e Informática, en cuyos talleres se pudieron realizar todos los ensayos mostrados.

---

Bibliografía

Altabba, B. (2000). Re-creating the Rainbow Bridge. Civil Engineering, 70(5), 32.

Azzi Visentini, M. (1980). I ponti di Palladio. Milano, IT: Electa.

Ceraldi, C., y Russo Ermolli, E. (2004). Timber arch bridges: a design by Leonardo. En Roca, P., y Oñate, D., eds., Arch Bridges IV: Advances in Assessment Structural Design and Construction (pp. 69-78). Barcelona: CIMNE.

Cerveró Meliá, E., Ferrer Gisbert, P. S., y CapuzRizo, S. F. (2016). Teoría, métodos y técnicas para el diseño de sistemas técnicos en la obra de Leonardo da Vinci. En: Proceedings From the 20th International Congress on Project Management and Engineering Cartagena, 13-15th July 2016 (pp. 1231-1241). Cartagena: Asociación Española de Dirección e Ingeniería de Proyectos.

Da Vinci, L. (2019). La macchina del mondo. Milano, IT: BUR Biblioteca Univ. Rizzoli.

Freire Tellado, M. J., Muñoz Vidal, M., López César, I., y Pérez Valcárcel, J. (2019). Estructuras desplegables de aspas para cubiertas inclinadas. Informes de la Construcción, 71(556), e311.

Foley, V. y Soedel, W. (1986). Leonardo’s Contributions to Theoretical Mechanics. Scientific American. 3(255), 108-113.

Funis, F. (2000). Il ponte ligneo sul Cismon e le altre tre invenzioni di Palladio. Bollettino ingegneri, 12, 7-18.

Gancedo, C. (2011). Once máquinas e ingenios de Leonardo da Vinci interpretados y realizados por Carlos Gancedo. Somió, Gijón, España: Fundación Museo Evaristo Valle.

Heyman, J. (2000). Palladio’s wooden bridges. Architectural Research Quarterly, 4(1), 81-86.

Hutchings, I. M. (2016). Leonardo da Vinci s studies of friction. Wear, 360, 51-66.

Keele, K. D. (2014). Leonardo da Vinci’s Elements of the science of man. London, UK: Academic Press.

Kemp, M. (2006). Leonardo da Vinci: Experience, experiment and design. London, UK: V & A Publications.

Marinoni, A. (2000). Il Codice Atlantico. Firenze, IT: Giunti.

Pedretti, C. (1978). Leonardo architetto. Milano, IT: Electa.ç

Pérez Valcárcel, J. y Escrig Pallarés, F. (1994). Pioneering in expandable structures: the Madrid I’ notebook by Leonardo da Vinci. Bulletin of the International Association for Shell and Spatial Structures, 35(1), 33-45.

Pérez Valcárcel, J., Freire-Tellado, M. J., y MuñozVidal, M. (2019). Estructuras desplegables para actividades lúdicas. Bac Boletín Académico. Revista de investigación y arquitectura contemporánea, 9, 129-146. P

isano, R. (2013). Reflections on the scientific conceptual streams in Leonardo da Vinci and his relationship with Luca Pacioli. Advances in Historical Studies, 2(02), 32.

Pizzigoni, A. (2010). Leonardo and the reciprocal structures [internet]. Disponible en: http://www.pizzigoni.it/leonardo%20Eng.pdf

Reti, L. (1967a). The Leonardo da Vinci codices in the Biblioteca Nacional of Madrid. Technology and culture, 8(4), 437-445.

Reti, L. (1968a). The Two Unpublished Manuscripts of Leonardo Da Vinci in the Biblioteca Nacional of Madrid-I. The Burlington Magazine, 110(778), 10-12.

Reti, L. (1968b). The Two Unpublished Manuscripts of Leonardo da Vinci in the Biblioteca Nacional of Madrid-II. The Burlington Magazine, 110(779), 81-91.

Russo Ermolli, E., y Mormone, E. (1996). Struttura e intuizione statica prima della rivoluzione tecnica del XVII secolo. Adrastea, 7, 4-15.

Sánchez Sánchez, J., Escrig Pallarés, F., y Rodríguez León, M. T. (2010). Una aproximación analítica a las mallas recíprocas diseñadas por Leonardo. Informes de la Construcción, 62(518), 5-14.

Sánchez Sánchez, J., Escrig Pallarés, F., y Rodríguez León, M. T. (2014). Reciprocal Tree-Like Fractal Structures. Nexus Network Journal, 16(1), 135-150.

Scantamburlo, A. C., Moraes, E. L., Rocha, G., Esteves, S. S. L., Reis, T. S. R., y de Campos, L. C. (2017). Building the Da Vinci’s Self Supporting Bridge. En: Deus Júnior, G. A., et al., eds. Alive Engineering Education: Transforming and Innovating Engineering Education (pp. 29-35). Goiâna, BR: Gráfica UFG.

Sotomayor Castellanos, J.R., Villaseñor Aguilar, J.M., Aoi, H. et al. (2007). Investigación e Ingeniería de la Madera. Publicación del Laboratorio de Mecánica de la Madera. División de Estudios de Posgrado. Morelia, Michoacán, MX: Universidad Michoacana de San Nicolás de Hidalgo.

Tampone, G. (2001). Acquaintance of the ancient timber structures. En Lourenço, P. B., y Roca, P., eds., Historical Constructions (pp. 117-144). Guimarães, PT: University of Minho.

Tampone, G. (2005). I ponti di legno. Tradizione e innovazione nel Rinascimento. En Ponti: Sorveglianza, manutenzione e interventi, Seminario Centro Internazionale di Aggiornamento Sperimentale, Florencia [internet]. Disponible en: http://www.cias-italia.it/PDF/133.pdf

Usher, A. P. (1929). A History of Mechanical Invention. New York, US: McGraw-Hill.

White, M. (2002). Leonardo: el primer científico. Barcelona: Plaza & Janés.

Yang, Y., Chen, B., y Gao, J. (2007). Timber arch bridges in China. En Proceedings of the Fifth International Conference on Arch Bridge (pp. 171-178). Guimarães, PT: University of Minho, Department of Civil Engineering.

Yang, Y., Nakamura, S., Chen, B., y Nishikawa, T. (2012). Traditional construction technology of China timber arch bridges. J