Diseño de un recipiente cilíndrico mediante el motor evolutivo Wallacei

Lucas García Menéndez_1, María del Mar Espinosa Escudero_2, Manuel Domínguez Somonte_3

Resumen
En el presente trabajo se desarrolla un nuevo modelo para el diseño de un recipiente cilíndrico de 250 ml de capacidad. Se busca utilizar la mínima cantidad de material posible para la fabricación del recipiente y, al mismo tiempo, dotarle de una base los más voluminosa posible. Con este fin, se emplea el lenguaje de programación visual Grasshopper 3D y el motor evolutivo Wallacei. Se exploran las diferentes opciones de la herramienta y, una vez realizada la simulación, se seleccionan y analizan las soluciones más significativas.

Palabras clave: Diseño generativo, algoritmos genéticos, optimización multiobjetivo, Grasshopper 3D, Wallacei.

Abstract
In the present work, a new model for the design of a cylindrical container with a capacity of 250 ml is developed. The aim is to use the minimum amount of material possible to manufacture the container and, at the same time, provide it with a base as much voluminous as possible. To this end, the Grasshopper 3D visual programming language and the evolutionary Wallacei engine are used. The different options of the tool are explored and, once the simulation has been carried out, the most significant solutions are selected and analyzed.

Keywords:  Generative design, genetic algorithms, multiobjective optimization, Grasshopper 3D, Wallacei.

---

Lucas García Menéndez1, María del Mar Espinosa Escudero2, Manuel Domínguez Somonte3
Recibido / received: 15/08/2020. Aceptado / accepted: 03/03/2021.
1. Graduado en Ingeniería Mecánica por la Universidad de Oviedo (2019). Especializado en diseño mecánico y fabricación. Ingeniería del Diseño. Universidad Nacional de Educación a Distancia (UNED).
2. Profesora de la Escuela Técnica Superior de Ingenieros Industriales de la Universidad Nacional de Educación a Distancia (UNED), en el departamento de Ingeniería de Construcción y Fabricación. Profesora y coordinadora del Máster Universitario en Ingeniería del Diseño.
3. Profesor de la Escuela Técnica Superior de Ingenieros Industriales de la Universidad Nacional de Educación a Distancia (UNED), en el departamento de Ingeniería de Construcción y Fabricación. Profesor del Máster Universitario en Ingeniería del Diseño.
Código Unesco del área de conocimiento: 3313 (Tecnología e Ingeniería Mecánica)
Autor para correspondencia: Lucas García Menéndez. lgarcia2715@alumno.uned.es.

---

Introducción
Los algoritmos evolutivos constituyen una herramienta muy adecuada para la resolución de problemas de optimización multiobjetivo (Deb, 2001). Dichos algoritmos se basan en los postulados de la evolución biológica. Las entidades que representan las posibles soluciones al problema se denominan individuos o cromosomas, y el conjunto de estos, población. Los individuos son modificados por operadores genéticos, principalmente el cruce, que consiste en la mezcla de la información de dos o más individuos; la mutación, que es un cambio aleatorio en los individuos, y la selección, consistente en la elección de los individuos que sobrevivirán y conformarán la siguiente generación. Dado que los individuos que representan las soluciones más adecuadas al problema tienen más posibilidades de sobrevivir, la población va mejorando gradualmente (Makki, 2015; Navarro-Mateu, Makki y Cocho-Bermejo, 2018).

En el presente trabajo se desarrolla un modelo basado en algoritmos genéticos para el desarrollo de un recipiente cilíndrico. El diseño tiene dos objetivos: utilizar la mínima cantidad de material posible (para una capacidad de 250 ml) y concentrar el mayor volumen de material en la base para aumentar su estabilidad. Es, por tanto, un problema de optimización multiobjetivo. Para la ejecución se emplea el motor evolutivo Wallacei. Esta herramienta permite a los usuarios ejecutar simulaciones evolutivas en el lenguaje de programación visual Grasshopper 3D (plug-in que corre dentro de la aplicación CAD Rhinoceros 3D). Lanzado en enero de 2018, Wallacei incorpora potentes herramientas analíticas y métodos de selección de soluciones que ayudan a los usuarios a comprender mejor los procesos evolutivos y a tomar decisiones de forma eficiente. Además, Wallacei ofrece a los usuarios la posibilidad de seleccionar, reconstruir y obtener cualquier fenotipo de la población una vez completada la simulación (Wallacei, 2019; Rutten, 2010).

El principal componente de la plataforma Wallacei se llama Wallacei X. Esta herramienta permite ejecutar un algoritmo evolutivo, analizar los resultados, implementar métodos de selección y exportar fenotipos, todo ello dentro de una misma interfaz de usuario. Wallacei X emplea el algoritmo NSGA-2 (Deb et al., 2002) como algoritmo evolutivo primario, y el método k-medias como algoritmo de agrupación (Wallacei, 2019).

Desarrollo
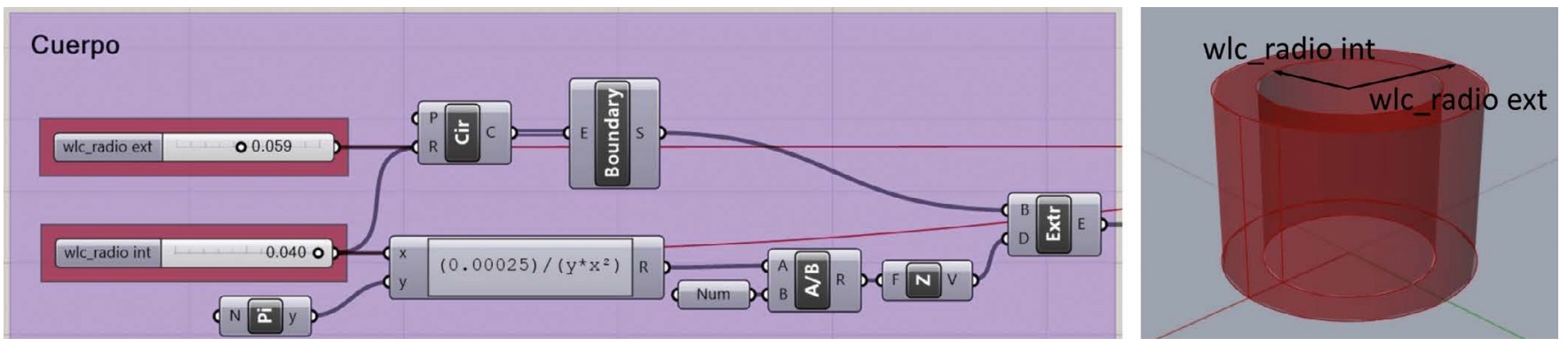
Como se mencionó anteriormente, la definición de la geometría se lleva a cabo mediante el lenguaje de programación visual Grasshopper 3D. El recipiente, objeto del problema, está formado por dos partes: el cuerpo y la base. Como muestra la figura 1, la geometría está construida de tal forma que el radio interior y el exterior del cuerpo se controlan a través de dos sliders (identificados como wlc_radio int y wlc_radio ext, respectivamente). Sea cual sea el valor del radio interno, la capacidad del recipiente debe mantenerse en 250 ml (0,00025 m3 ). Para conseguir esto, la altura del cuerpo se obtiene a partir de dicho radio y de la fórmula del volumen de un cilindro.

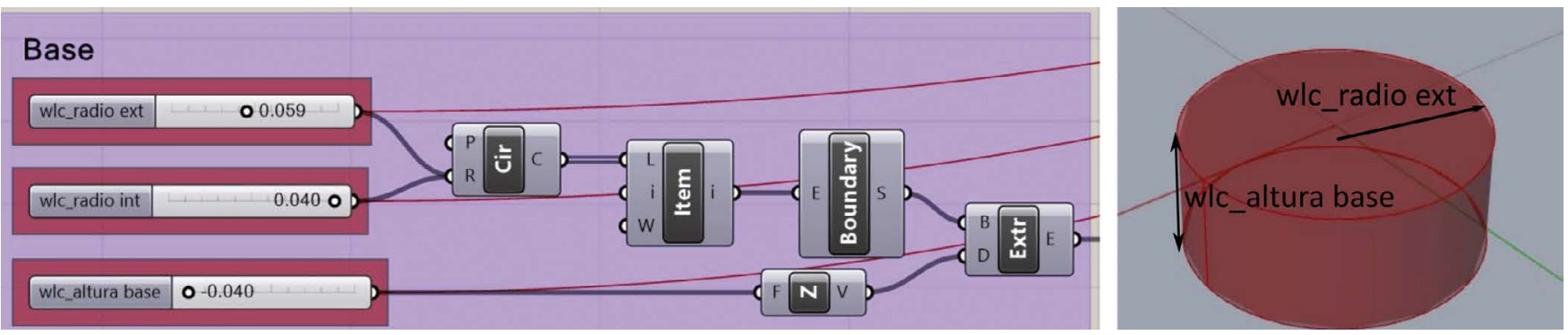
La base está formada por un cilindro cuyo radio coincide con el radio exterior del cuerpo. Como se muestra en la figura 2, la altura de la base se controla con un tercer slider (denominado wlc_altura base). Mediante la unión de ambas partes se obtiene la geometría final del recipiente.

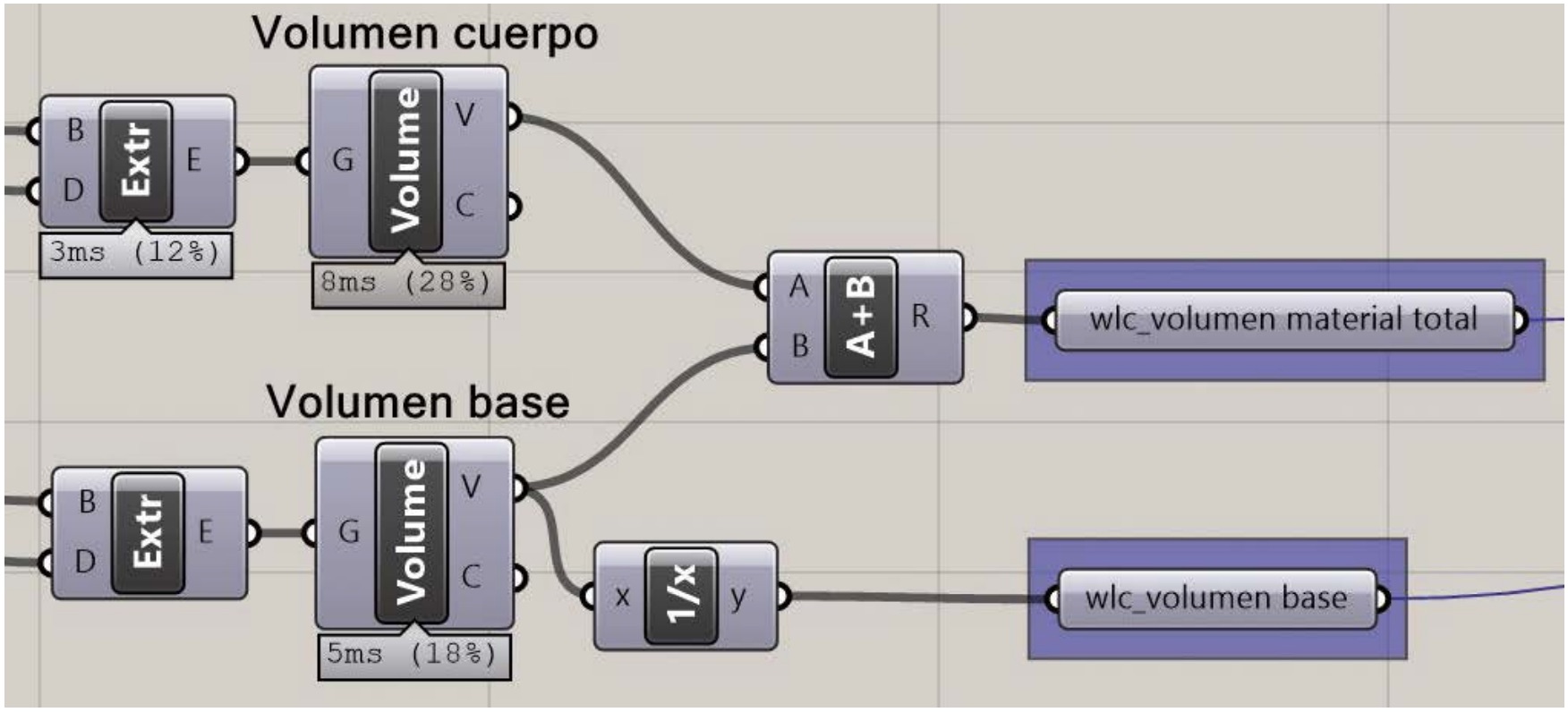
Los datos de salida del componente extrusión (Extr en figuras 1 y 2) son del tipo BREP (o b-rep) (Stroud, 2006), por lo que el volumen se puede calcular directamente con el componente de Grasshopper volume (Fig. 3). Lógicamente, la suma del volumen del cuerpo y del volumen de la base constituye el volumen de material necesario para la fabricación de un recipiente. En la definición mostrada en la figura 3, dicho valor viene identificado como wlc_volumen material total. El volumen de la base del recipiente se encuentra bajo el nombre wlc_volumen base.

Una vez obtenida una geometría inicial, se tienen que definir los genes y los objetivos del algoritmo evolutivo, los cuales constituyen las dos entradas esenciales de las cuatro del componente Wallacei X. Los genes corresponden con los sliders mencionados anteriormente, es decir, la altura de la base y los radios interno y externo del cuerpo del recipiente. Los objetivos son el volumen total de material necesario para fabricar el recipiente y la inversa del volumen de la base (componentes resaltados en azul de la figura 3). El motor evolutivo moverá los sliders para minimizar los objetivos.

Para configurar el algoritmo, en primer lugar, se define el número de soluciones por generación (tamaño de la generación) y el número de generaciones que forman la población total. El tamaño de la población es la multiplicación de ambos. En el ejemplo propuesto, se han fijado ambos valores a 20, por lo que la población está compuesta de un total de 400 soluciones

Resultados
En la mayoría de los casos de optimización multiobjetivo no hay un valor que produzca un óptimo de forma simultánea para cada uno de los objetivos que componen la función. Esto se debe a la existencia de conflictos entre objetivos, que hace que la mejora de uno de ellos dé lugar a un empeoramiento de otro. En el caso que nos proponemos, teniendo en cuenta que los objetivos son maximizar el volumen de la base y minimizar el volumen de material necesario para la fabricación del recipiente, un aumento del volumen de la base traería consigo un incremento del volumen del material. Habrá que llegar, por tanto, a una situación de compromiso en la que todos los objetivos sean satisfechos en un grado aceptable, desde el punto de vista del diseño.

A diferencia de los problemas de optimización con un único objetivo, el concepto de óptimo es ahora relativo y será necesario decidir de alguna forma cuál es la mejor solución (o cuáles son las mejores soluciones) al problema (Steuer, 1986) (Sawaragi, Nakayama y Tanino, 1985).

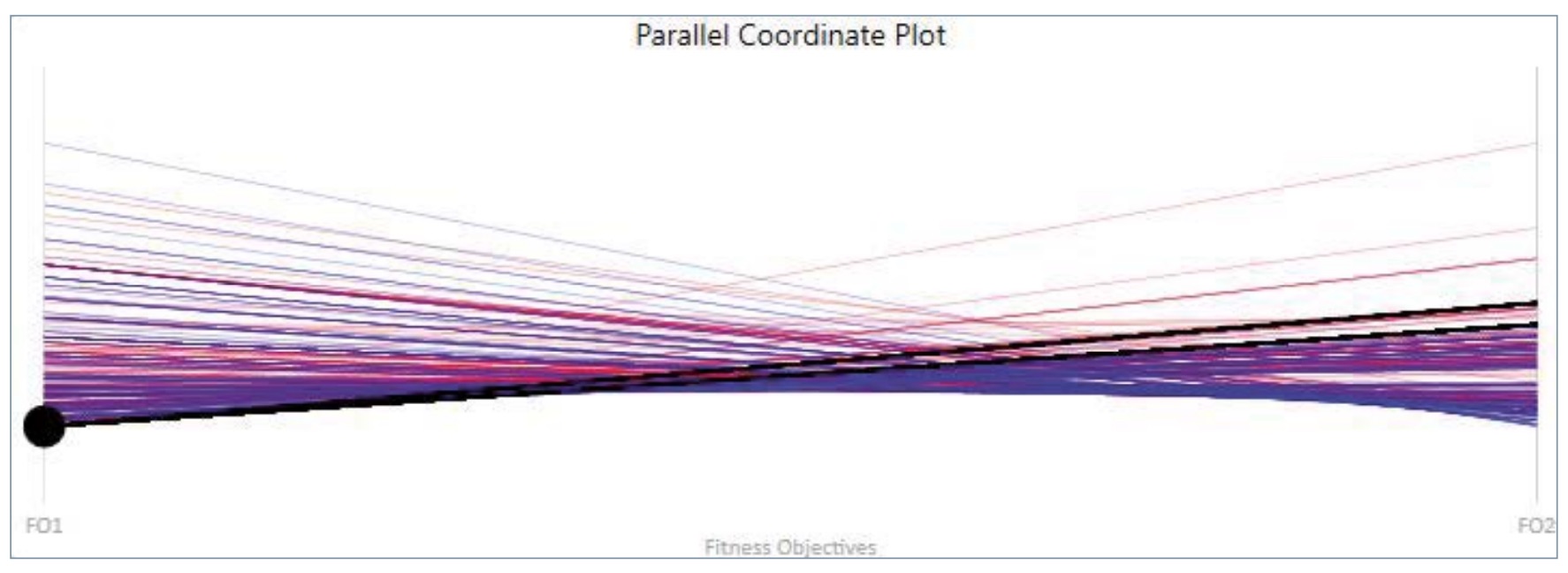
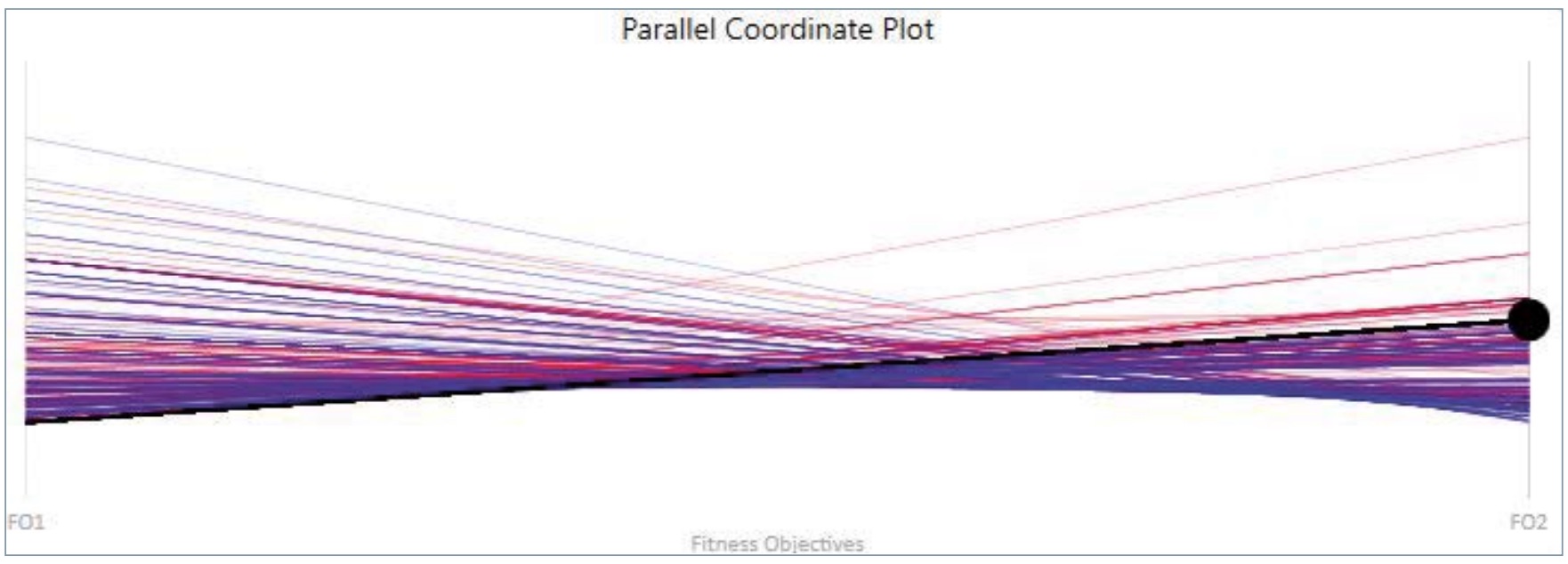
Wallacei X proporciona numerosas herramientas analíticas para seleccionar las soluciones que se desean exportar. Las gráficas de coordenadas paralelas (Parallel Coordinate Plot) se utilizan para trazar datos numéricos multivariados. En un gráfico de coordenadas paralelas, cada variable recibe su propio eje y todos los ejes se colocan en paralelo entre sí. Cada eje puede tener una escala diferente, ya que cada variable trabaja con una medida diferente, o todos los ejes pueden normalizarse para mantener todas las escalas uniformes. Los valores se representan como series de líneas conectadas a través de cada eje. En el caso propuesto, la gráfica constará únicamente de dos variables (una por cada objetivo de optimización) y representará todas las soluciones obtenidas. El gráfico de coordenadas paralelas analiza todas las soluciones de la población mediante la comparación de los valores de aptitud para cada solución en todos los objetivos.

El componente de análisis de gráficos de coordenadas paralelas de Wallacei X cuenta con cuatro métodos de análisis (Wallacei, 2019), de los cuales utilizamos los dos más significativos.

Soluciones con los valores de aptitud más repetidos
Se extraen las soluciones asociadas a los valores de aptitud (fitness values) más repetidos en la población. Los valores de aptitud son los diferentes valores que toman los objetivos del problema de optimización.

De las 400 soluciones obtenidas, para el objetivo 1, es decir, maximizar el volumen de la base del recipiente, el valor de aptitud más repetido es 1.624,025187m-3, que ha aparecido 37 veces. Como se ha mencionado, el algoritmo siempre minimiza los objetivos de aptitud, por lo que para maximizar el volumen de la base el algoritmo minimiza la inversa de dicho volumen. Por tanto, el volumen de la base más repetido es:

Para el segundo objetivo, es decir, minimizar el volumen de material total, el valor de aptitud más repetido es 0,001131 m3 , un total de 24 veces.

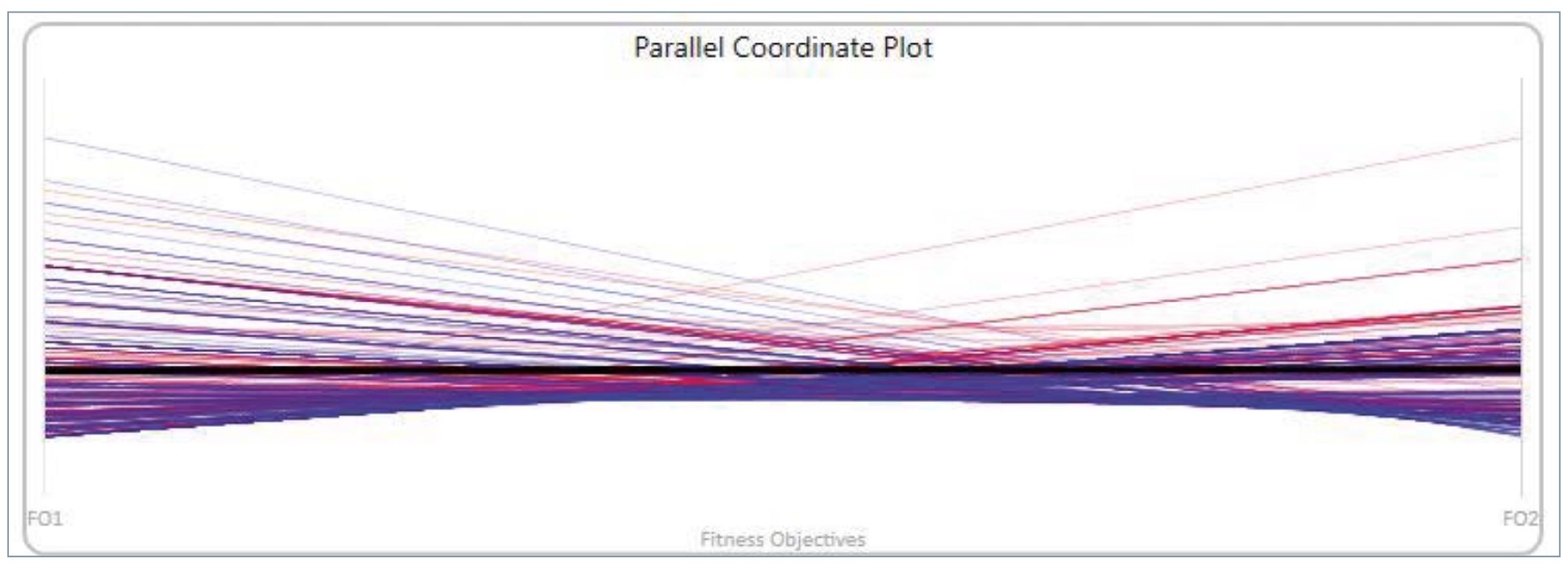
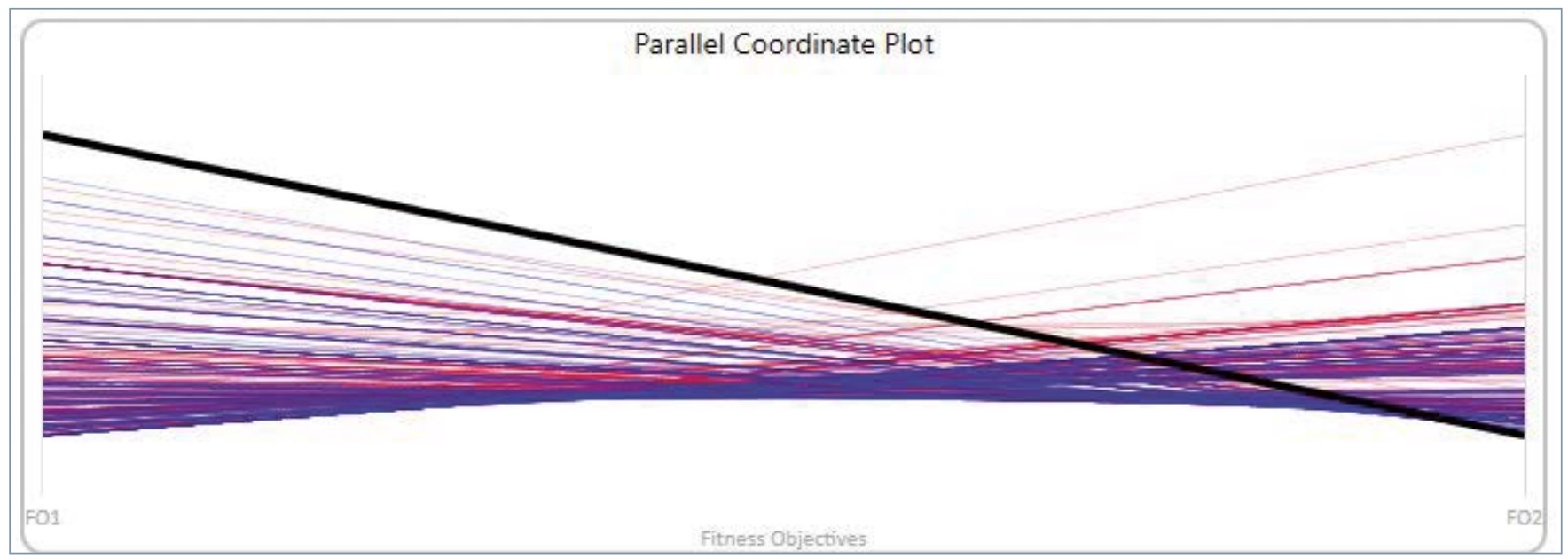
Diferencia relativa entre rangos de aptitud
Tras clasificar las soluciones por orden de aptitud de tal forma que el 0 represente la solución más apta, este método ordena las soluciones de acuerdo con la diferencia relativa entre las posiciones de los diferentes objetivos. La solución más apta es la que tenga el mismo puesto en todos los objetivos, es decir, aquella en la que no haya diferencia entre los dos puestos. Lógicamente, la solución que Figura 6. Solución más apta. Figura 7. Solución con mayor diferencia relativa entre objetivos. está en la misma posición en los dos objetivos es una recta. Para dicha solución, el volumen de material es 0,000813 m3 y el de la base 0,000282 m3 .

De 400 soluciones obtenidas (clasificadas de la posición 0 a la 399), la que presenta mayor diferencia entre puestos de la clasificación es la que se muestra en la figura 7. En este caso, el volumen de material tiene un valor de 0,000286 m3 , mientras que el volumen de la base es 0,000097 m3 .

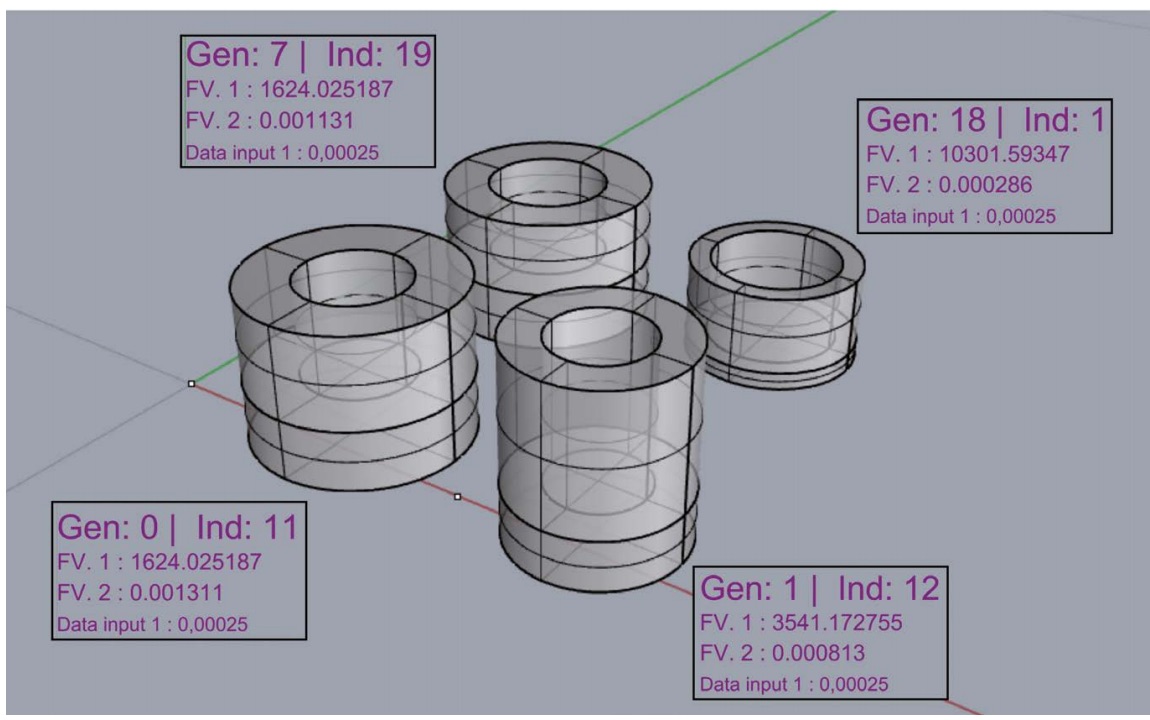
En lugar de reconstruir los fenotipos (es decir, obtener la geometría asociada a cada resultado) para toda la población (400 resultados en nuestro caso), se reconstruyen solo para las cuatro soluciones específicas seleccionadas con los métodos anteriores (Fig. 8).

Las soluciones correspondientes al individuo 0 de la generación 11 y al individuo 7 de la generación 19 son las extraídas con el primer método, valores de aptitud más repetidos, mientras que las correspondientes al individuo 1 de la generación 12 y al individuo 18 de la generación 1 fueron extraídas con el segundo, diferencia relativa entre rangos de aptitud.

Como muestra la figura 9, el volumen del contenido del recipiente (Data input 1) es siempre 0,00025 m3 o, lo que es lo mismo, 250 ml.

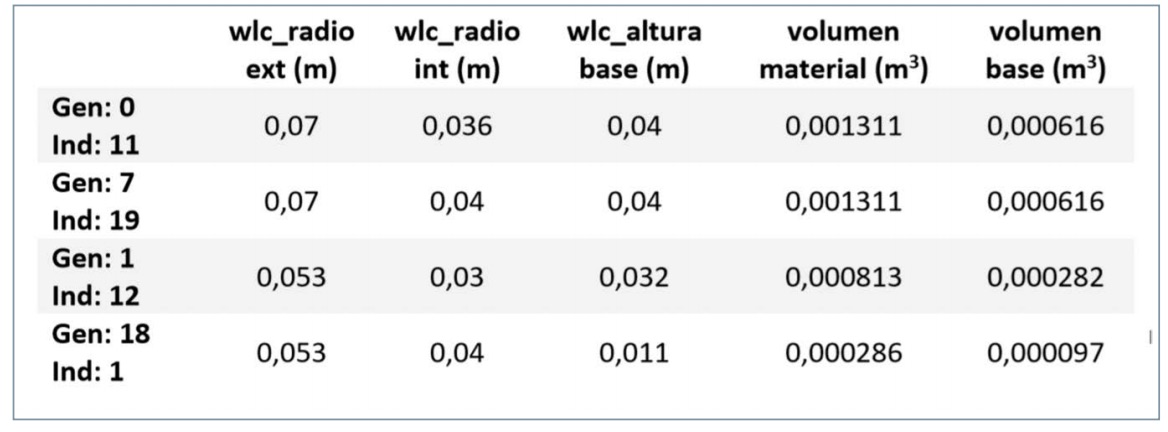
Por último, la tabla 1 recoge los valores que adoptan los sliders que controlan la geometría del recipiente junto con los volúmenes de material y de la base correspondientes.

Como se puede apreciar en la tabla 1 y en la figura 9, las dos primeras soluciones tienen los mismos valores para los dos objetivos de optimización, es decir, tanto el volumen de la base como el total son iguales. Sin embargo, hay diferencias dimensionales en las geometrías asociadas a esas soluciones. El radio interior de la solución 0 de la generación 11 es 4 mm menor que el de la solución 19 de la generación 7. Teniendo en cuenta que la capacidad del recipiente debe ser constante e igual a 250 ml, esta reducción en el radio se traduce en un aumento de la altura del cuerpo.

Conclusiones
Gracias al lenguaje de programación visual Grasshopper 3D y al motor evolutivo Wallacei X, se ha planteado un problema de optimización multiobjetivo en el que se buscaba diseñar un recipiente cilíndrico de 250 ml de capacidad con la mínima cantidad de material posible. Además, se quiere que la mayor parte de material se concentre en la base del recipiente.

Como se ha explicado a lo largo de este trabajo, no existe una solución única para el problema planteado. Es ahí donde entra en juego el objetivo del diseño y la visión del diseñador, quien tiene que decantarse por una solución u otra. De las cuatro geometrías extraídas, se elegiría la solución 1 de la generación 18 si se buscase el ahorro de material. Si, por el contrario, prevaleciera la robustez del recipiente proporcionada por una base voluminosa, habría que decantarse por la solución 11 de la generación 0 o la solución 19 de la generación 7.

Otro factor a tener en cuenta es el uso del objeto que se va a diseñar. Por ejemplo, en determinadas aplicaciones un gran grosor en el cuerpo del recipiente (es decir, una gran diferencia entre el radio exterior y el interior) puede suponer un aspecto negativo, por lo que habría que descartar gran parte de las soluciones obtenidas. Una línea de trabajo futuro podría ser la incorporación de aspectos de esta naturaleza a la definición del problema, de tal forma que las soluciones se enfoquen a aplicaciones concretas.

El ejemplo expuesto en este trabajo ha demostrado las inmensas posibilidades que nos brinda la herramienta Wallacei X. El empleo de algoritmos evolutivos ha permitido explorar una gran cantidad de soluciones, muchas de las cuales no se hubieran obtenido mediante métodos de diseño tradicionales.

---

Bibliografía

Deb, K. (2001) Multi-objective optimization using evolutonary algorithms. 1.a ed. New York: John Wiley & Sons.

Deb, K., Pratap, A., Agarwal, S. y Meyarivan, T. (2002) «A fast and elitist multiobjective genetic algorithm: NSGA-II», IEEE Transactions on Evolutionary Computation, 6(2), pp. 182-197.

Makki, M. (2015) «An Evolutionary Model for Urban Development Urban», en International Seminar on Urban Form. Rome, Italy.

Navarro-Mateu, D., Makki, M. y Cocho-Bermejo, A. (2018) «Urban-tissue optimization through evolutionary computation», Mathematics, 6.

Rutten, D. (2010) Evolutionary Principles applied to Problem Solving using Galapagos. Disponible en: https://www.grasshopper3d.com/profiles/blogs/ evolutionary-principles (accedido: 6 de julio de 2020).

Sawaragi, Y., Nakayama, H. y Tanino, T. (1985) Theory of multiobjective optimization. Orlando: Academic Press.

Steuer, R. E. (1986) Multiple criteria optimization: theory, computation, and application. New York: John Wiley & Sons.

Stroud, I. (2006) Boundary Representation Modelling Techniques. Springer-Verlag Lodon.

Wallacei (2019) «Wallacei: an Evolutionary and Analytic Engine for Grasshopper 3D. Primer 2.0».