Detección de la posición y tamaño de una grieta mediante impacto-eco y MCSD
Detecting size and position of a crack by impact-echo and MCSD
R. Medina (1), P. García-Albaladejo (1), F. Barrio-Parra (1), B. Biosca (1), J. Díaz-Curiel (1), L. Arévalo-Lomas (1)
Resumen
El presente trabajo plantea el uso combinado del método de impacto-eco y el algoritmo MCSD multicross spectral density (MCSD) para la detección en placas de hormigón de la posición y el tamaño de grietas paralelas a la superficie. El método de impacto-eco se basa en analizar, tras generar ondas mediante un impacto sobre los materiales que se pretenden evaluar, las reflexiones que se producen en las superficies, interfases y defectos internos de los mismos. Se realiza la simulación mediante el programa de elementos finitos Ansys® y se estudia la respuesta para diferentes longitudes de grieta con relación a la distancia a la superficie. Se emplean elementos infinitos para simular contornos laterales absorbentes, lo que permite simular placas de gran tamaño sin coste computacional. Las ondas que generan el impacto y sus múltiples reflexiones se recogen en varios transductores. La posición del impacto y la localización de los captadores se varían desde una posición centrada respecto de la grieta hasta una localización exterior a la misma. Las señales se tratan en el dominio del tiempo y posteriormente en el dominio de la frecuencia mediante la Transformada Rápida de Fourier (FFT) y el algoritmo MCSD. Comparando para los diferentes casos los valores que se obtienen para las amplitudes a la frecuencia de eco característica de la grieta con los valores a la frecuencia de eco característica del fondo de la placa, se obtiene información sobre la posición del punto de impacto y de los transductores con respecto al borde de la grieta, pudiéndose estimar la posición y longitud de la grieta.
Palabras clave: Hormigón, Impacto-eco, Grietas, Métodos no destructivos, Método de elementos finitos, Elementos infinitos, Transformada de Fourier, Propagación de ondas.
Abstract
This work proposes the combined use of the impact-echo method and the multicross spectral density (MCSD) algorithm for the detection of defects in concrete slabs, particularly cracks parallel to the surface, which determine their depth and size. The impact-echo method is based on analyzing, after generating waves through an impact on the materials to be evaluated, the reflections that occur on their surfaces, interfaces and internal defects. The Ansys® finite element program is used to model a plate with cracks parallel to the surface, the waves generated by a mechan- ical impact on the surface and the response for different crack lengths in relation to the distance to the surface. Infinite elements are used to simulate absorbing lateral contours. This allows sim- ulating large plates without computational cost. The waves generated by the impact and its multiple reflections are collected in several transducers (eight on each side of the impact), and they are distributed equidistantly on the surface and collect information in the time domain. Subsequently, these signals are processed and passed to the frequency domain using the Fast Fourier Transform (FFT) and the MCSD algorithm, which performs the cross spectral density of the signals coming from the transducers.
Keywords: Concrete, Impact-echo, Cracks, Nondestructive testing, Finite element method, Infinite elements, Fourier transform, Wave propagation.
Recibido / received: 20/06/2021. Aceptado / accepted: 26/10/2021.
1 Departamento de Energía y Combustibles. ETSIME. Universidad Politécnica de Madrid (UPM).
Autor para correspondencia: Rafael Medina, e-mail: rafael.medina@upm.es
Introducción
El método de impacto-eco [1] se basa en el estudio de la propagación de ondas de tensión transitorias generadas por un impacto elástico de corta duración. Se realiza de forma mecánica contra la superficie del material mediante una bola de acero de pequeño diámetro (de entre 4 y 15 mm). Se generan tensiones de baja frecuencia que se propagan por la estructura y son reflejadas por defectos del material y superficies externas. Las señales que representan los desplazamientos en la superficie son recogidos en el dominio del tiempo por un transductor próximo al impacto y, posteriormente, son transformadas al dominio de la frecuencia mediante la transformada de Fourier. La componente del desplazamiento que resulta de interés es la componente perpendicular a la superficie, que es la que detectaría un transductor de onda P. Las múltiples reflexiones de las ondas de tensión en las interfases y en los contornos se registran en el espectro y se usan para identificar las características del material y sus posibles defectos. El método es especialmente adecuado para ciertos medios heterogéneos (hormigón, asfalto) donde habitualmente se usan métodos destructivos, dado que otros métodos no destructivos (ultrasonidos) no dan buenos resultados, pues las altas frecuencias que emplean son fuertemente atenuadas por este tipo de medios.
Si una onda se propaga con una velocidad cp por el material y la reflexión se produce en una zona situada a una distancia d de la superficie, la frecuencia ft de la llegada a la superficie (frecuencia de eco) es
siendo ? un coeficiente que depende de la geometría y el material; para placas de hormigón se estimó experimentalmente en 0.96. Estudios posteriores sobre la relación entre esta frecuencia de eco y la frecuencia correspondiente a la velocidad de grupo cero de las ondas Lamb [2,3] permiten extender esta fórmula a placas de cualquier otro material, y se obtiene el valor de ? a partir del coeficiente de Poisson del material.
El espectro de frecuencias contiene, a menudo, picos que no son fáciles de interpretar. El hecho de que la reflexión de las ondas longitudinales sobre un contorno genere tanto ondas longitudinales como transversales, sumado a las propias ondas transversales generadas en el impacto, provoca la aparición de interferencias entre las diferentes ondas que dificultan la interpretación del espectro. Los picos no deseados del espectro pueden reducirse o incluso eliminarse mediante técnicas de procesamiento de señal. En este trabajo se empleó el algoritmo MCSD (multicross spectral density) para dicho propósito [4]. Las señales se registran en n detectores en lugar de en un único punto y son combinadas en el dominio de frecuencia para obtener su señal MCSD, definida como
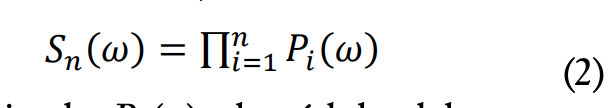siendo Pi (w) el módulo del espectro de la señal registrada por el detector i. Mediante este algoritmo se logra que solo se mantengan aquellos picos de frecuencia que tienen amplitudes elevadas en todos los detectores, eliminándose, así, las frecuencias que provienen de interferencias.
El método de impacto-eco presenta problemas adicionales de interferencias que se deben a los rebotes en los contornos laterales de la placa [5]. Si el tamaño de esta no es mucho más grande que el espesor las reflexiones en los contornos, especialmente de la onda Rayleigh, interfieren con las reflexiones de la onda P y dificultan poder ver con claridad en el espectro la frecuencia de eco. Para evitar esto habría que emplear, por tanto, placas de elevada relación longitud a espesor, lo que elevaría el coste de computación. Además, si el ensayo se quiere hacer para simular una placa en la que la relación longitud a espesor no fuera elevada, parece que el método no funcionaría.
Es habitual [6-8] el empleo de la técnica de impacto-eco para obtener a partir de la frecuencia de eco ft la posición en profundidad d de una grieta sin más que despejar de la ecuación (1). Para poder ser detectada [9], el espesor de la grieta debe ser como mínimo de 0,08 mm y el ancho de la grieta debe ser mayor que un tercio de la distancia a la superficie. Sin embargo, el método no permite estimar el tamaño de la grieta ni su posición respecto al punto de impacto. Hay algunos trabajos relativos a este tema [10-13], pero aplican técnicas que no obtienen los resultados directamente a partir de la frecuencia de eco.
En atención a todo lo anterior, el objetivo fundamental de este trabajo es obtener, además de la posición en profundidad de una grieta, habitual en el método de impacto-eco, información acerca del tamaño y de la posición de una grieta respecto al punto de impacto, a partir de las amplitudes de las frecuencias de eco correspondientes a la reflexión en la grieta y en la superficie inferior de la placa. Adicionalmente, se persigue resolver el problema de las interferencias debidas a rebotes en los contornos laterales de la placa mediante el empleo de elementos absorbentes que eviten la reflexión de las ondas, para lo que se van a utilizar elementos infinitos en los contornos laterales. El empleo de estos elementos hace posible, además, estudiar placas de alta relación longitud a espesor, con bajo coste de computación.
El conocimiento del tamaño y de la posición de la grieta, y no solo su profundidad, mejoraría el uso del método de impacto-eco en actividades en las que ya se emplea y se abre la posibilidad de nuevas aplicaciones. Puede usarse para evaluar la integridad de pavimentos, como en las capas de asfalto sobre hormigón de la pista de un aeropuerto, donde un mal contacto entre ambas capas (que equivaldría a la presencia de una gran grieta horizontal) puede suponer graves problemas no solo económicos sino de seguridad. Puede aplicarse a la detección de grietas en túneles, que pueden haber sido causadas por el agua, impactos de obras cercanas o vibraciones debidas al paso de trenes o vehículos, grietas cuyo tamaño debe ser monitorizado continuamente en las operaciones de mantenimiento, sobre todo para prevenir fugas de agua que afecten al túnel. O, de manera similar, en la detección y control del tamaño de grietas en una presa de hormigón. En la reparación de estructuras de mampostería, se puede aplicar para la detección y evaluación mediante métodos no destructivos de grietas que puede haber en los edificios. Y puede aplicarse en temas medioambientales, para estudiar cómo se produce la migración de vapores contaminados desde el suelo a las viviendas, donde un factor muy importante para determinar el grado de intrusión es el porcentaje y la conectividad de las grietas de la cimentación, o el mal contacto que puede existir entre el suelo y las paredes del edificio, que supondrían un camino de penetración del vapor. Determinar el tamaño de esos malos contactos influiría en una mejor estimación de los parámetros que se utilizan en los modelos que calculan la concentración de vapores en los edificios y realizan una evaluación de riesgos.
Metodología
Para el desarrollo del trabajo se han realizado modelizaciones con el software de elementos finitos Ansys®, empleando placas en dos dimensiones suponiendo deformación plana, dado que los resultados permitirían demostrar la utilidad del método y se reduce de manera muy importante el coste de computación respecto a una modelización en 3D. Se emplea para ello el elemento finito PLANE182 de Ansys®. Se ha supuesto contorno libre en las superficies superior e inferior de la placa.
Para los contornos laterales de la placa se han empleado elementos absorbentes para poder trabajar con placas de menor longitud y, a la vez, evitar las reflexiones en los contornos, especialmente de la onda Rayleigh. El método utilizado para ello ha sido emplear elementos infinitos (INFIN257 en Ansys®) en dichos contornos, para lo que ha sido necesario desarrollar un programa en lenguaje APDL de Ansys®. Para comprobar el correcto funcionamiento de estos elementos, se realiza una simulación en una placa sin grieta para comprobar la atenuación de la señal al llegar a los contornos y verificar que la frecuencia de eco se detecta con claridad.
Se ha simulado que las placas son de hormigón de densidad ?= 2.500 kg/ m3 , con un módulo de elasticidad E = 30,47 GPa y coeficiente de Poisson v= 0,25, lo que da una velocidad de onda P c p = 3.824 m/s. El coeficiente ? correspondiente, teniendo en cuenta el valor del coeficiente de Poisson [2,3], puede considerarse de 0,94.
Las características comunes de las placas son 1,2 m de espesor y 5 m de longitud. Hay que tener en cuenta que en los contornos laterales se emplean elementos absorbentes, lo que permite que estas dimensiones puedan simular una placa de gran longitud. Se van a simular grietas de diferentes anchuras que se van a colocar siempre a una profundidad de 50 cm. De los valores anteriores y de la ecuación (1) se pueden determinar las frecuencias teóricas de eco de la grieta, 3.595 Hz, y de la superficie inferior de la placa, 1.498 Hz.
La variación de la fuerza del impacto con el tiempo de una pequeña esfera sobre la superficie puede representarse mediante medio periodo de una función seno cuadrado. El tiempo de contacto t c depende del radio de la esfera y del material con el cual se impacta; en los ensayos habituales suele estar en el rango entre 15 y 100 ms. El contenido en frecuencia de dicho impacto se obtiene a partir de la transformada de Fourier de la señal, de donde puede deducirse que la máxima frecuencia útil es del orden de 1,25/t c . El impacto se simula introduciendo esta fuerza sinusoidal en el nodo elegido de la superficie del material.
El tiempo de muestreo Dt de la señal es el inverso de la frecuencia de Nyquist, igual al doble de la máxima frecuencia de interés f máx , y que, a su vez, deberá ser mayor que la frecuencia de eco de la grieta f;
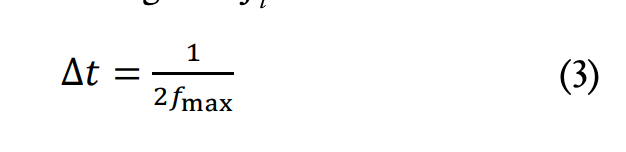El mallado debe ser suficientemente fino para poder representar los efectos de la propagación de las ondas. La menor longitud de onda que detecta puede obtenerse a partir de la máxima frecuencia de interés f máx y la velocidad de propagación cp como
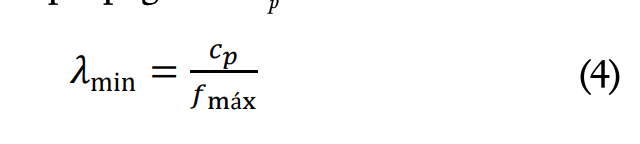Ansys® recomienda emplear como mínimo 10 elementos por longitud de onda.
El tiempo de contacto del impacto que se emplea en la modelización es de 35 ms, que correspondería a una esfera de 8 mm, lo que permite excitar frecuencias de hasta el orden de 35 kHz, que cumple ser más del doble de la frecuencia máxima de eco buscada (3.595 Hz). Se ha elegido un tamaño de mallado de 0,01 m, válido para una ?mín de 0,1 m y una f máx de hasta 38 kHz según la ecuación (4). El tiempo de muestreo Dt que se emplea es de 3,5 ms, con objeto de tener al menos 10 puntos de muestreo de la semisenoide de carga. Con este tiempo de muestreo, de la ecuación (3) se obtiene que la frecuencia máxima en el espectro es de 142.857 Hz, aunque debemos tener presente que con el impacto realizado solo se excitan frecuencias de hasta unos 35 kHz, en todo caso muy por encima de las frecuencias de eco buscadas.
La resolución en frecuencia de la señal es
siendo n el número de muestras tomadas (o nDt el tiempo total de registro). En nuestro caso se han tomado 4.096 muestras, para un tiempo de registro de 0,0143 s, lo que conduce a una resolución en frecuencia de 69,8 Hz.
Un problema adicional que resolver que ya aparece en los primeros trabajos sobre impacto-eco [6,7] es la necesidad de eliminar de la señal la onda Rayleigh directa, ya que la elevada energía que contiene altera totalmente el espectro y dificulta la detección de las frecuencias de eco. En este trabajo el procedimiento realizado consiste en la detección de la llegada de la onda Rayleigh a cada punto de medida, a partir del máximo desplazamiento vertical que se tiene en el registro la posterior de supresión de la onda en la seña. Una vez eliminada la onda Rayleigh, el resto de información ya es útil para poder determinar las frecuencias de eco. Para poder aplicar la ecuación (2) se van a colocar ocho detectores a la derecha y ocho más a la izquierda del punto de impacto en cada ensayo, en posiciones simétricas respecto al impacto. Para seguir las recomendaciones del método de impacto-eco [1] que sugiere que las mejores detecciones se logran a distancias del punto de impacto de entre el 20 % y el 40 % de la distancia a la que se produce la reflexión, el primero de los detectores se coloca a una distancia de 10 cm del impacto, con una separación de 2 cm entre cada uno de los demás.
de una grieta de 1 m con impacto fuera de la grieta
El procedimiento a seguir consiste en realizar impactos en diferentes posiciones de la superficie con respecto a la posición de la grieta, registrar las señales y observar la evolución de las frecuencias de eco del fondo de la placa y del fondo de la grieta para, a partir de ella, poder sacar conclusiones sobre la posición y tamaño de la misma. Se van a usar tres anchuras de grieta diferentes: 1 m, 50 cm y 30 cm (mayor, igual y menor que la profundidad a la que se encuentra). Se realizan simulaciones con un impacto situado en el centro de la grieta y con impactos desplazados hacia el borde de la grieta o fuera de ella.
Las señales recogidas por los detectores se procesan, filtrando previamente la onda Rayleigh, y calculando su transformada de Fourier (FFT). Con las transformadas obtenidas se calcula el MCSD de los ocho receptores a la derecha del impacto y de los ocho a la izquierda, de manera independiente. Se han filtrado las bajas frecuencias del espectro, que corresponden a modos propios de la placa y que suelen tener una amplitud elevada, para que puedan visualizarse correctamente las frecuencias de eco.
Análisis de resultados
Comportamiento de los elementos absorbentes
Para comprobar el correcto funcionamiento de los elementos infinitos como elementos absorbentes se ha realizado un ensayo de impacto sobre una plancha sin grietas, de las dimensiones y características indicadas en el apartado anterior.
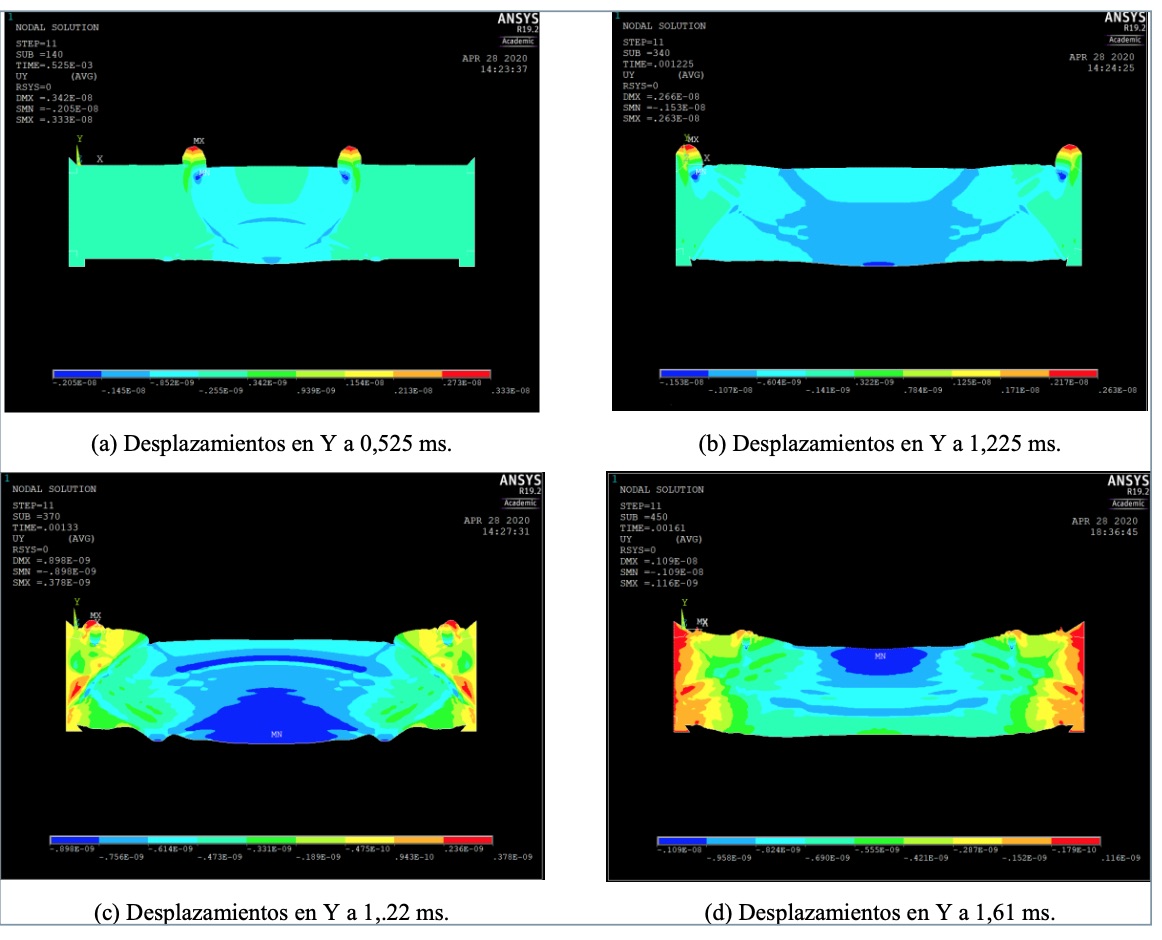
Tras el impacto en el centro de la placa las ondas se van propagando por la superficie y por el interior de la misma como se ve en la figura 1, en la que se reflejan los desplazamientos en la dirección Y. Los frentes de ondas pueden verse en la figura 1a, habiéndose reflejado ya en el fondo de la placa, pero antes de que lleguen al borde lateral. En la figura 1b se muestran los desplazamientos justo antes de reflejar en el contorno absorbente. El orden de magnitud de los máximos desplazamientos es de 0.2. 10-8 y corresponden a la onda Rayleigh (en color rojo). Al reflejarse en el contorno (figura 1c) los desplazamientos disminuyen al orden de 0.3.10-9. En la figura 1d, ya pasados 1,61 ms podemos ver cómo apenas aparece el desplazamiento debido a la onda Rayleigh en los puntos de la superficie, del orden de 0.2.10-9.
En la figura 2 se muestra el MCSD correspondiente a la modelización anterior, y puede observarse cómo se detecta la frecuencia de eco de la placa (1.465 Hz) sin que aparezca ningún otro pico en la señal que pudiera reflejar alguna interferencia. Los elementos infinitos actúan, por tanto, adecuadamente como elementos absorbentes de la onda Rayleigh.
Impacto en el centro de la grieta
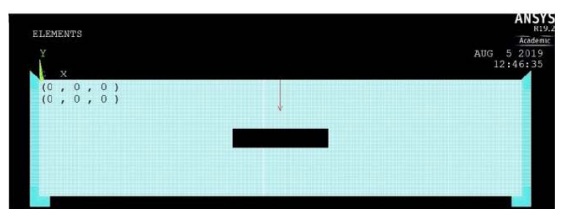
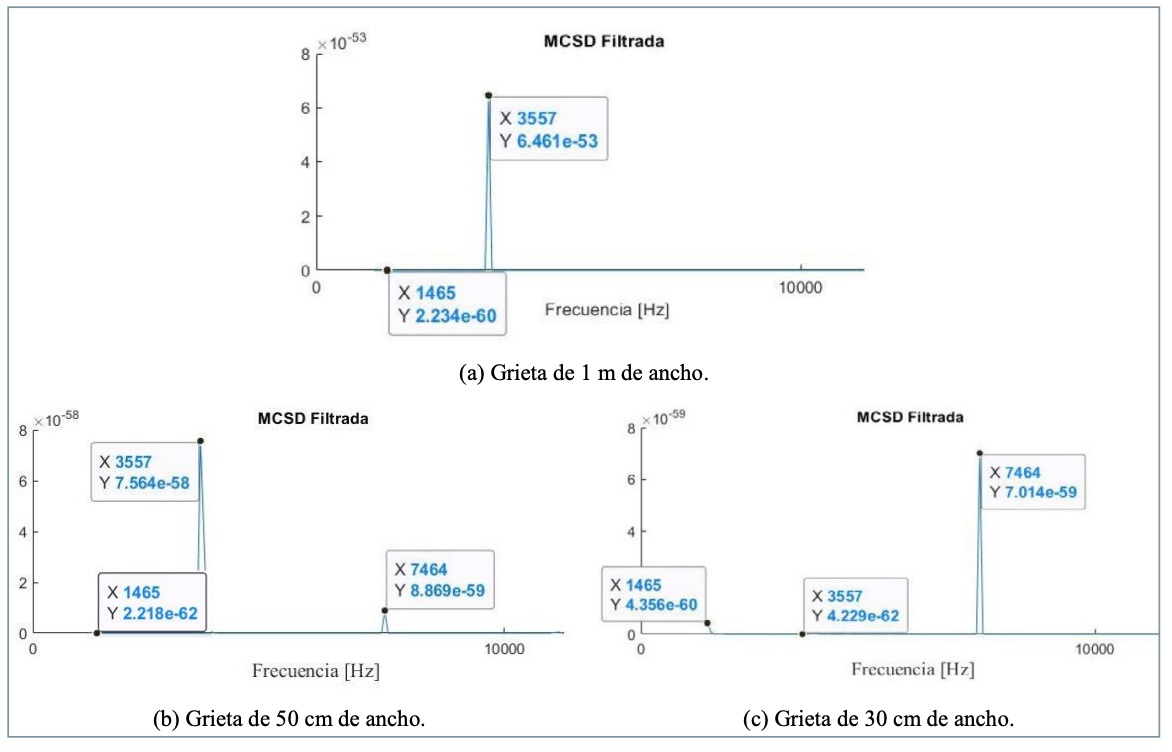
En la figura 3 se muestra el mallado y el impacto del primer caso que se plantea, con una longitud de grieta de 1 m, superior a la profundidad de la misma ( y = 50 cm) y, por tanto, fácilmente detectable por impacto-eco. Se ha simulado un impacto centrado en la placa y grieta (x = 2,5 m) y se han colocado los receptores en una posición inicial de 2,6 m (distancia del 20 % de la profundidad a la que se encuentra la grieta), espaciados cada uno 0,02 m hacia la derecha, por lo que el último receptor se encuentra en una posición de 2,74 m, todavía muy lejos del final de la grieta (que se encuentra en x = 3 m).
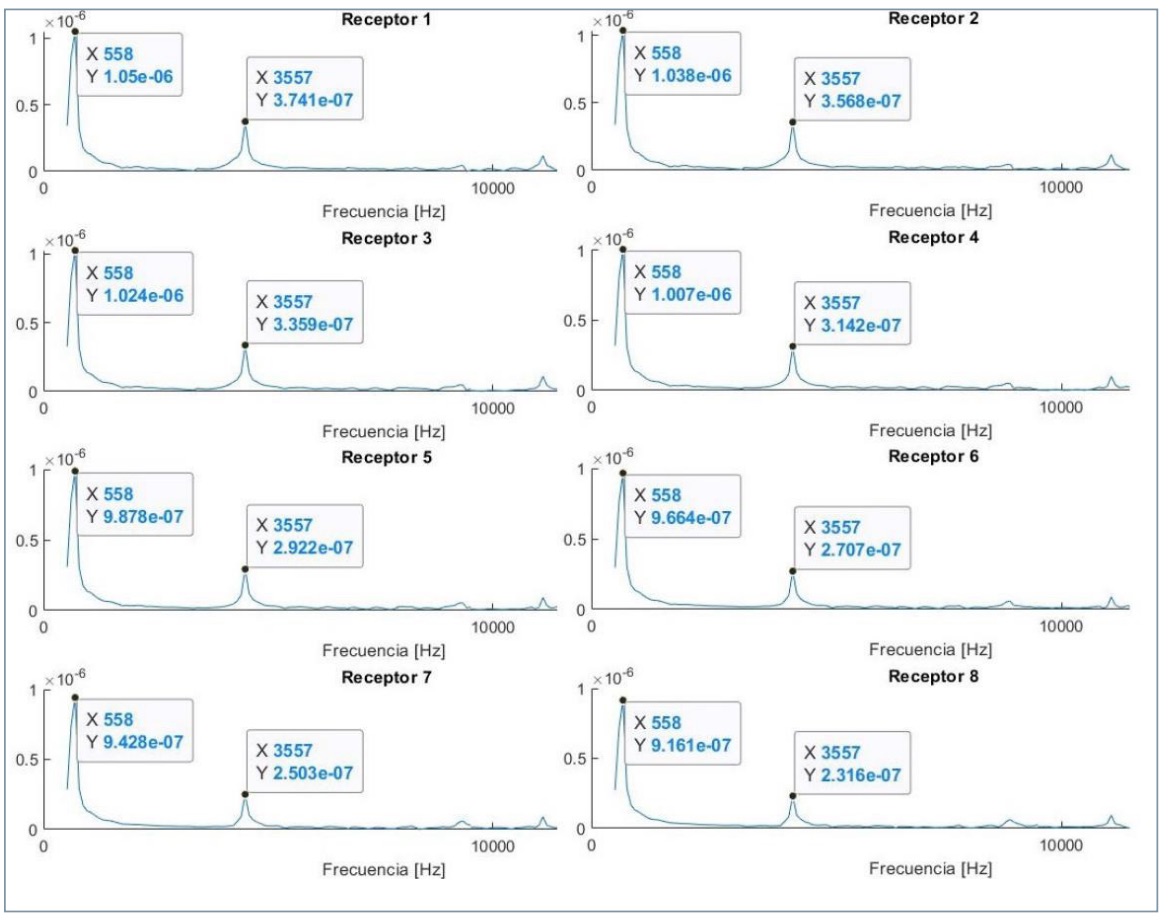
En la figura 4 se muestran las transformada de Fourier (FFT) de los desplazamientos en la dirección Y generados por la onda en los receptores situados a la derecha del impacto.
Puede observarse en todos ellos un pico a la frecuencia de 558 Hz, correspondiente a un modo propio de la placa y un pico a la frecuencia de 3.557 Hz, correspondiente a la frecuencia de eco de la grieta. No aparece ningún pico a la frecuencia de eco de la placa, lo cual indica que todos los detectores están sobre la grieta. Puede verse, además, que la amplitud de la frecuencia de eco de la grieta disminuye a medida que nos alejamos del centro de la misma.
En la figura 5 se muestran los MCSD de los 8 detectores a la derecha del impacto, tanto para la grieta de 1 m como para las de 50 y 30 cm de ancho. En ellos se ha filtrado el modo propio de la grieta mediante un filtro pasa-alta para poder observar mejor las frecuencias de eco. Comparando la figura 5a con la figura 4 se observa que, al haber eliminado la frecuencia de 558 Hz, puede detectarse la frecuencia de 1.465 Hz correspondiente a la frecuencia de placa, pero con un valor despreciable comparado con la frecuencia de eco de la grieta, lo que confirma que se está sobre la grieta. Si se obtienen, por otra parte, los resultados de los ocho detectores situados a la izquierda del impacto, los MSCD son los mismos que los de la figura 5, para las diferentes anchuras, esperable al estar el impacto centrado. Podemos deducir, por tanto, que a medida que nos acercamos al centro de una grieta, los MCSD de los detectores a la derecha y a la izquierda dan resultados cada vez más parecidos, siendo idénticos al situarnos justo en el centro.
Comparando la figura 5b con la figura 5a, se observa que la amplitud de los picos correspondientes a los ecos de la grieta y de la placa han disminuido y que, aunque la frecuencia de eco de la grieta sigue siendo varios órdenes de magnitud superior a la de la placa, la diferencia de magnitud es ahora menor, como consecuencia de que los receptores están más cerca del borde de la grieta. Para una grieta de anchura de 50 cm (igual a la profundidad de la misma), los detectores siguen estando sobre la grieta, pero el último de ellos, con x = 2,74 cm, está justo en el borde de la misma (x = 2,75 cm). Para la grieta de 30 cm (Figura 5(c), borde en x=2.65 cm y detectores entre 2.6 y 2.74 cm) ya hay más detectores fuera de la misma y se observa que el pico correspondiente a la frecuencia de eco de la placa es mayor que el de la grieta. Se concluye, por tanto, que cuando hay más detectores fuera de la grieta que sobre ella, la amplitud de la frecuencia de eco de la placa supera a la de la grieta y esto nos permitiría detectar la posición del borde de la grieta. También puede verse cómo la amplitud de los picos disminuye según decrece el ancho de la grieta.
En las Figuras 5b y 5c se puede observar que aparece un pico de frecuencia no esperada de 7.464 Hz, superior a la frecuencia de eco de la grieta. Este pico puede corresponder a un modo superior de las frecuencias de Lamb [14] y podría dificultar la interpretación de los espectros, especialmente en el caso de la grieta de 30 cm (ancho de la grieta inferior a su profundidad).
Impacto sobre la grieta no centrado
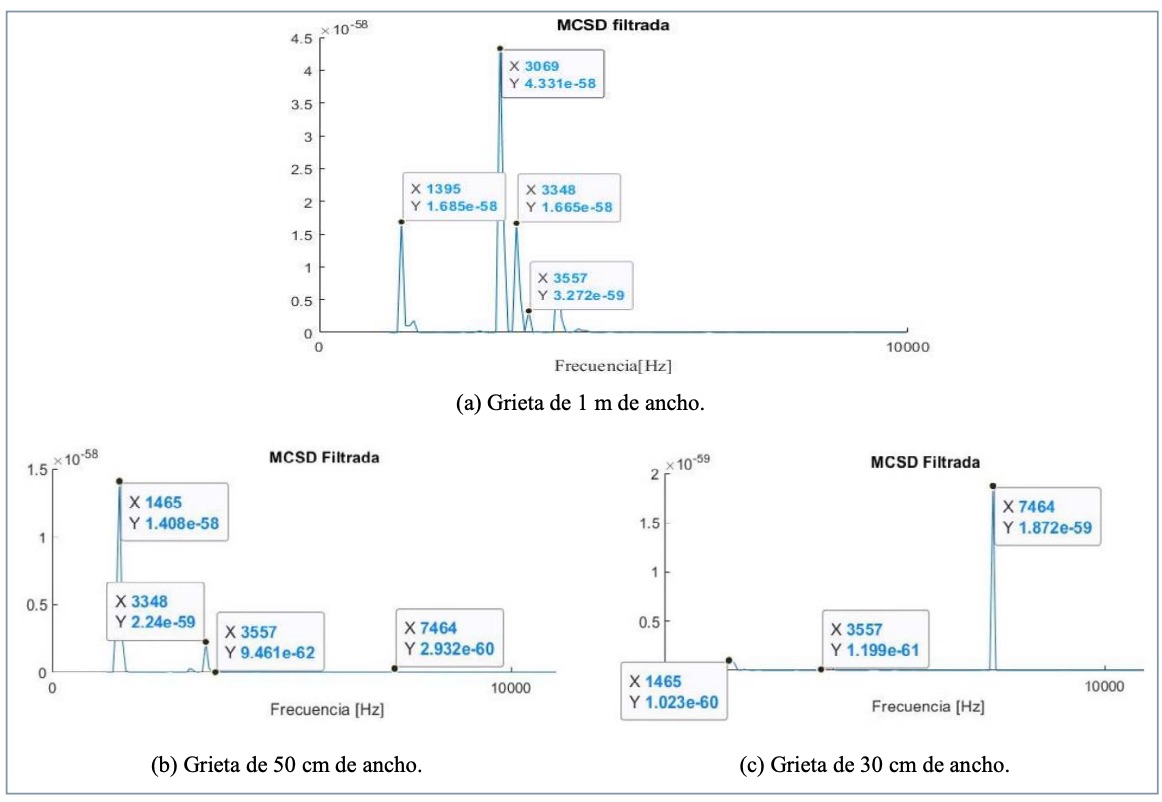
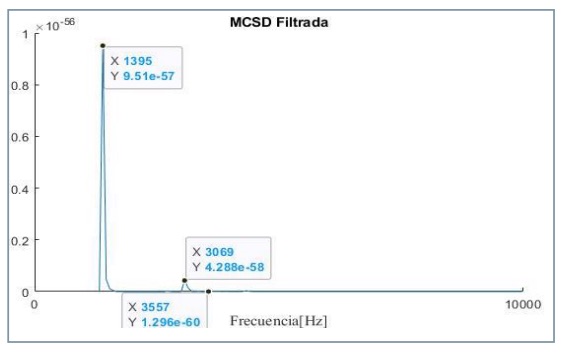
Se estudia aquí el caso de impactos situados sobre la grieta, pero alejados del centro de la misma, de manera que todos los receptores a uno de los lados del impacto (en este caso el lado derecho) queden fuera de la grieta. Se ha realizado para ello un impacto a 45 cm del centro en el caso de la grieta de 1 m (x = 2,95 cm, con el final de la grieta a 3 m), a 20 cm para la de 50 cm (x = 2,70 cm, con el final de la grieta a 2,75 cm) y a 10 cm para la de 30 cm (x = 2,60 cm, con el final de la grieta a 2,65 cm). En estos casos ninguno de los receptores a la derecha del punto de impacto se encuentra situado sobre la grieta.
En la figura 6 puede observarse como el MCSD para todos los casos muestra una frecuencia de eco de la placa (1.465 Hz, aunque en el caso de 1 m aparece a 1.395 Hz) con amplitud mayor (mínimo de un orden de magnitud) que la frecuencia de eco de la grieta (3.557 Hz). Esto se corresponde con que los receptores estén fuera de la grieta. La frecuencia de 3.557 Hz sigue apareciendo en el espectro, puesto que el impacto está sobre la grieta y parte de las reflexiones se producen en ella. Aunque no se muestran aquí, los resultados de los receptores situados a la izquierda del impacto dan un MCSD similar al mostrado en la figura 5, dado que todos ellos se encuentran sobre la grieta. El estudio conjunto de ambos MCSD nos llevaría a deducir que la posición del impacto está próximo al borde de la grieta.
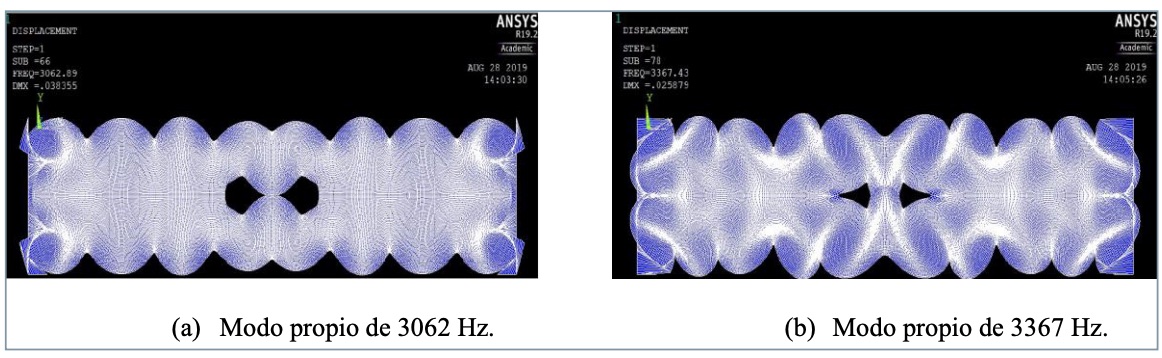
En las figuras 6b y 6c se vuelve a observar la aparición de la frecuencia de 7.464 Hz, ya comentada en el apartado anterior. En la figura 6a aparece una amplitud elevada a frecuencias de 3.069 y 3.348 Hz no esperadas. Se ha realizado un análisis modal y coinciden, teniendo en cuenta la precisión del espectro, con modos propios que son excitados por la posición del impacto. En la figura 7 se muestran ambos modos.
Impacto fuera de la grieta
Para confirmar lo detectado en el apartado anterior se ha realizado un impacto situado fuera de la grieta, aunque próximo al borde de ella. Obviamente, si el impacto se hiciera lejos de la grieta solo se detectaría la frecuencia de eco de la placa. Se ha realizado un impacto a 55 cm del centro para el caso de la grieta de 1 m (x = 3,05 cm, con el final de la grieta a 3 m). No se presenta el resultado en las otras grietas para no ser reiterativos. En la figura 8 se recoge el MCSD resultante en los detectores a la derecha del impacto (ninguno sobre la grieta). En ella puede observarse cómo el espectro es similar al del apartado anterior, pero se eleva aún más la amplitud de la frecuencia de eco de la placa respecto de la de la grieta: en el caso anterior era de un orden de magnitud y ahora de casi 4.
Conclusiones
El presente trabajo muestra la utilidad del método de impacto-eco para determinar la posición y la anchura de una grieta paralela a la superficie de una placa.
Se sabe que la posición en profundidad se puede detectar con este método. En el trabajo se muestra, sin embargo, que cuando el tamaño de la grieta disminuye con relación a la profundidad de la misma, aparecen picos de frecuencia que no corresponden con las frecuencias de eco y que podrían confundir y llevar a dar valores erróneos para dicha profundidad.
El uso de elementos infinitos como elementos de contorno absorbentes se ha comprobado útil para eliminar la onda Rayleigh, que es la que provoca más interferencias con las señales de eco provenientes del fondo de la placa y de la grieta, y que, tradicionalmente, dificulta la interpretación de las señales. El uso de los mismos permite, además, simular placas de gran anchura con un bajo coste de computación.
Se ha visto que es posible determinar dónde está el centro de una grieta colocando detectores a las mismas distancias a derecha e izquierda del impacto. Cuando el MCSD registrado a ambos lados coincida, indicará que el impacto está en el centro de la grieta. El MCSD resulta más cómodo que el uso de la FFT, dado que una única señal recoge la información de todos los detectores, además de eliminar las posibles interferencias.
Mientras los detectores están sobre la grieta, prácticamente solo aparece la frecuencia de eco de la grieta. Las amplitudes de dicha frecuencia son menores cuanto menor es el tamaño de la grieta. De esta forma se puede saber que no se ha llegado al borde de una grieta y tener ya una estimación del tamaño de la misma.
A medida que el impacto se acerca al borde de la grieta, aumenta la amplitud de la frecuencia de eco de la placa respecto de la frecuencia de eco de la grieta. Cuando hay más detectores que no están situados sobre la grieta, la frecuencia de eco de la placa es de mayor amplitud, lo que permitiría detectar el final de la grieta. Se sigue verificando que las amplitudes de ambas frecuencias disminuyen con el tamaño de la grieta.
Cuando ni el impacto ni los detectores están sobre la grieta la frecuencia de eco de la grieta prácticamente no se detecta y la frecuencia de eco de la placa tiene mucha más amplitud.
Una dificultad que aparece en el estudio es que los impactos excitan los modos propios de la placa, lo que hace necesario realizar un filtrado de dichos modos propios. Normalmente es fácil hacerlo, dado que sus frecuencias están por debajo de las frecuencias esperadas y se resuelve empleando un filtro pasa-alta. Sin embargo, en ocasiones, como ha ocurrido con la grieta de 1 m de ancho, se excitan modos propios de orden superior que dificultan la interpretación del espectro y es necesario identificar mediante análisis modal.
Agradecimientos
Los autores agradecen la financiación de este trabajo por el programa de investigación CARESOIL-CM (P2018/ EMT-4317) de la Comunidad de Madrid.
Referencias
[1] Sansalone M., “Impact-Echo: The Complete Story”, ACI Structural Journal 94, 777-785 (1997).
[2] Gibson A., Popovics J.S., “Lamb wave basis for impact-echo method analysis”, Journal of Engineering Mechanics 131 (4), 438-443 (2005).
[3] Medina R., Bayón A., “Elastic constants of a plate from impact-echo resonance and Rayleigh wave velocity”, Journal of Sound and Vibration 329, 2114-2126 (2010).
[4] Medina R., Garrido M., “Improving impact-echo method by using cross-spectral density”, Journal of Sound and Vibration 304, 769-778 (2007).
[5] Medina R., Garrido M., “Numerical modelling of the impact-echo method for materials characterisation”, Damage & Fracture Mechanics VII, 273–282, Southampton (2003).
[6] Sansalone M., Carino N.J., “Transient impact response of plates containing flaws”, Journal of Research of the National Bureau of Standards 92 (6), 369-381 (1987).
[7] Abraham O., Lonard C., Cote P., Piwakowski B., “Time frequency analysis of impact-echo signals: numerical modelling and experimental validation”, ACI Materials Journal 97 (6), 645-657 (2000).
[8] Hsiao C., Cheng C.C., Liou T., Juang Y., “Detecting flaws in concrete blocks using the impact-echo method”, NDT&E International 41, 98-107 (2008).
[9] Cheng C.C., Sansalone M., “Determining the minimum crack width that can be detected using the impact-echo method”, Materials and Structures 28, 74-82 (1995).
[10] Ali Shah, A., Ribakov, Y., “Non-destructive measurements of crack assessment and defect detection in concrete structures”, Materials and Design 29, 61-69 (2008).
[11] Yeh P., Liu P., “Imaging of internal cracks in concrete structures using the surface rendering technique”, NDT and E International 42, 181-187 (2009).
[12] Aggelis D.G., Kordatos E.Z., Strantza M., Soulioti D.V., Matikas T.E., “NDT approach for characterization of subsurface cracks in concrete”, Construction and Building Materials 25, 3089-3097 (2011).
[13] Eremin A., Golub M., Glushkov E., Glushkova N., “Identification of delamination based on the Lamb wave scattering resonance frequencies”, NDT and E International 103, 145-153 (2019).
[14] Prada C., Clorennec D., Royer D., “Local vibration of an elastic plate and zero-group velocity Lamb modes”, J. Acoust. Soc. Am. 124, 203-212 (2008).
