Desarrollo de una metodología de detección de grietas de fatiga en ruedas ferroviarias basada en el análisis de frecuencias naturales
Resumen
El objeto de este trabajo es el análisis modal de una rueda ferroviaria con grietas y el estudio de la evolución del comportamiento de los modos de vibración a fin de reducir el número de accidentes causados por ello. Se abordará el modelado realista, en PTC Creo 3.0, de una rueda ferroviaria, siguiendo las especificaciones de una rueda real, al que se le practicarán grietas de diferentes tamaños en las posiciones más propicias al fallo. Se consideran dos tipos de defectos: grietas radiales y grietas circunferenciales. Se analiza la evolución de las frecuencias naturales y se generan curvas de ajuste que describen la evolución de frecuencias como una función del área de la grieta. La metodología está basada en el análisis de las pendientes y los coeficientes de correlación asociados y permitiría especificar los modos más propicios, donde la evolución de la grieta ocasiona un comportamiento frecuencial más uniforme. Estos modos serían los elegidos para establecer el estado de la rueda ferroviaria y poder detectar la presencia de grieta y el tamaño de la misma.
Palabras clave
Frecuencias naturales, grietas de fatiga, metodología, rueda ferroviaria.
Abstract
This paper presents the development of a new methodology for fatigue cracks detection in railway wheels, analyzing the evolution of the eigenfrequencies as a function of crack size. Two types of defects are considered: radial cracks and circumferential cracks. The evolution of the natural frequencies is analyzed, and trend lines are generated, describing the evolution of the eigenfrequencies as a function of crack area. This methodology is based on the analysis of the slopes and associated correlation coefficients of the trend lines. This would allow for the determination of the favorable modes, in which the growth of the crack causes uniform variations in the values of the eigenfrequencies. These modes would be chosen to evaluate the structural integrity of the railway wheel and to detect the presence and size of the cracks.
Keywords
Eigenfrequencies, fatigue crack, methodology, railway wheel.
Recibido / received: 06.06.2018 Aceptado / accepted: 16.06.2018.
Introducción
Las ruedas ferroviarias son componentes mecánicos sometidos a altos niveles de carga estática y dinámica en condiciones normales de servicio. Esas car-gas generan tensiones y deformaciones cíclicas responsables de la aparición de grietas por fatiga después de un determinado periodo de funcionamiento. Estas grietas alteran la integridad estructural, modifican las características vibratorias de las ruedas y producen una bajada de las frecuencias naturales y una modificación del comportamiento vibratorio. Las grietas generadas pueden propagarse hasta causar la rotura de la rueda en servicio, lo que puede causar un accidente catastrófico, con daños y pérdidas considerables. Es el caso del accidente que se produjo en Eschede, en el norte de Alemania en 1998 (Esslinger V. et al., 2004). Investigaciones posteriores demostraron que la rotura de una rueda fue la causa principal del accidente.
Debido a ese accidente y los que siguieron, se iniciaron los proyectos WIDEM (WIDEM Project, 2008) y EURAXLES (EURAXLES Project, 2010), pertenecientes al sexto y séptimo proyecto marco de la UE, respectivamente. Con el proyecto EURAXLES, se pretende reducir el riesgo de fallo de los ejes montados a nivel mínimo, con los costes de mantenimiento en un nivel razonable y minimizando el riesgo de interrupción de servicio, de modo que no sea considerado una amenaza significativa para la operación segura del material rodante dentro del espacio europeo. En cuanto al proyecto WIDEM, el objetivo final era aumentar la competitividad, la capacidad y la disponibilidad del material rodante europeo, especialmente el de los ejes montados.
Del proyecto WIDEM se obtuvo, entre otros resultados, una nueva metodología de inspección no destructiva basada en la resonancia compensada. Se emplea la excitación artificial de los modos propios de un eje ferroviario en una banda de frecuencia definida (10-150 kHz) para detectar fallos mecánicos, en el laboratorio o en servicio (WIDEM Project, D2S International, 2008), analizando las frecuencias propias y los amortiguamientos modales. La metodología propuesta en el proyecto WIDEM se basa en el hecho de que cualquier defecto en un componente mecánico reduce su rigidez, provoca disminución de sus frecuencias naturales y altera sus modos de vibración. Este cambio en las propiedades vibratorias está relacionado con la forma y el tamaño del defecto. Por tanto, detectando esa variación en los modos propios de vibración es posible determinar la condición de integridad estructural del elemento bajo estudio.
En este trabajo se plantea la aplicación a ruedas ferroviarias de una técnica original, basada en el mismo principio descrito anteriormente, que distribuye las frecuencias naturales en el ámbito de las vibraciones mecánicas (vibraciones medibles con un acelerómetro) en lugar de llegar hasta frecuencias ultrasónicas. De este modo, se pretende que la inspección pueda realizarse en servicio, midiendo solo las vibraciones, sin necesidad de desmontar la rueda ferroviaria, lo que garantizaría un mantenimiento más sencillo y rápido y menos costoso.
Metodología
Como planteamiento del problema, se debe decir que se pretende detectar la condición de integridad estructural de una rueda ferroviaria en servicio a partir del estudio de la evolución de sus frecuencias naturales según va creciendo un defecto incipiente. El objetivo primordial es diferenciar las ruedas defectuosas que podrían tener un fallo prematuro en servicio de aquellas que no tienen defectos analizando las frecuencias naturales.
El estudio y el análisis de las frecuencias naturales de la rueda defectuosa se lleva a cabo en las etapas siguientes: en primer lugar, se realiza un modelado completo de las ruedas ferroviarias. Se define la geometría de la pieza, el material que la constituye y los tipos de defectos que se quieren detectar. Las figuras 1 y 2 ilustran los dos tipos de defectos considerados en este trabajo: las grietas radiales y las grietas circunferenciales. En segundo lugar, se procede al mallado de los modelos y a la definición de las condiciones de contorno, se realizan las configuraciones del análisis modal y se ejecutan los análisis. Luego se extraen los datos de frecuencias obtenidos de las simulaciones y se preparan para un posprocesado mediante tablas Excel.
El procesado de datos se lleva a cabo comparando los resultados obtenidos para el caso de la rueda sana y los de las ruedas agrietadas. Se elaboran tablas y gráficas comparativas, calculando diferencias porcentuales que muestran la evolución de las frecuencias naturales en función de los parámetros y posición de los defectos. Por regresión lineal, se determinan funciones lineales que permiten predecir la evolución de las frecuencias naturales en función del nivel de defecto, expresado como área de la grieta. Finalmente, se realiza un análisis de las pendientes y coeficientes de correlación para una discriminación y selección de los modos de vibración más fiables para la representación de defectos.
Modelado y generación de grietas
La rueda se modela en PTC CREO Parametric 3.0 según las formas y dimensiones de una rueda real. El material utilizado es el acero ER7 cuyas características vienen dadas en (UNE -EN 13979-1:2006 + A2:2011, 2011).
Las propiedades mecánicas son: densidad , límite elástico: , Resistencia última a tracción: , módulo de Young: , coeficiente de Poisson: . Las ruedas ferroviarias suelen presentar varios tipos de defectos (v. defectología descrita en Molina Sánchez, B., 2006). En este trabajo se examinan dos tipos de defectos: la grieta radial y la grieta circunferencial.
Las grietas radiales (Fig. 1) se inician en la banda de rodadura y se pro-pagan hacia el interior de la rueda en dirección radial. Se supone que las grietas cubren toda la superficie des-de una cara de la rueda hasta la cara opuesta. Las grietas circunferenciales (Fig. 2) aparecen en la zona de transición entre la llanta y el cubo. Es una zona peligrosa donde el momento de flexión alternado causa grietas de fatiga en el interior de la rueda. Se desarrollan circunferencialmente como se puede observar en la figura 2.
Como se puede observar en las figuras 1 y 2, los parámetros de la grieta radial son el radio de la rueda , la longitud de la grieta y la superficie de la grieta. En el caso de la grieta circunferencial, los parámetros son el ángulo central , la posición radial de la grieta , la longitud de la grieta igual al producto del ángulo central por la posición radial y la superficie de la grieta. Siguiendo las recomendaciones de (Cantini, S. y Beretta, S., 2011), se procede a calcular las superficies de las grietas. Es un parámetro que permite un estudio comparativo de los resultados de los análisis modales sin tener en cuenta la forma de la grieta. Las tablas 1 y 2 muestran las variaciones de las superficies de las grietas en función de la porción del radio o de la circunferencia afectada por la grieta.
Se consideran un total de 11 longitudes para simular el avance de la grieta radial, desde una longitud de grieta correspondiente al 1% del radio, hasta el 84%. Para la grieta circunferencial, 10 longitudes son consideradas, del 1% al 50% de la circunferencia a la posición radial considerada.
Análisis modal
Una vez obtenidos los modelos, se procede a realizar el análisis modal. Las ruedas son consideradas libres, sin restricciones. Para el mallado, se consideran elementos tetraédricos de tamaño máximo de 50 mm. Se refinan las zonas de posible concentración de tensiones como los frentes de las grietas. Por cada modelo, se extraen los 40 primeros modos naturales.
Resultados
Se han realizado un total de 41 simulaciones: 11 simulaciones para el caso de la grieta radial, cada una representando un avance de grieta, y 30 simulaciones para el caso de la grieta circunferencial, considerando 3 posiciones de grietas y 10 avances para cada grieta. En este trabajo solo se presentan los resultados relativos a la posición radial. Por cada simulación, se extraen las 40 primeras frecuencias naturales. Se han obtenido 1.640 datos de frecuencias. Hay que apuntar que los valores de 0 Hz de los 6 primeros modos de vibración corresponden a los 6 grados de libertad de la rueda en el espacio, por lo que se desestiman para el análisis de los resultados y conclusiones futuras.
Para los dos tipos de grietas, se presentan solo los resultados de algunos modos de vibración. Los demás resultados son muy similares para el resto de los casos y ubicaciones estudiados.
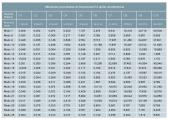
Las tablas 3 y 4 presentan los valores de las 25 primeras frecuencias naturales de la rueda sana y de las ruedas agrietadas. Se observa que a medida que aumenta el tamaño de la grieta disminuyen las frecuencias de vibración de los distintos modos como consecuencia de la reducción de la rigidez de la misma rueda, como lo predice la teoría.
A continuación, se procede a calcular las diferencias porcentuales de las frecuencias, para todos los casos, respecto al caso de la rueda sin defectos, según la ecuación (1).
Al realizar esta operación, se obtienen las tablas 5 y 6 que permiten apreciar las disminuciones de las frecuencias. El análisis detallado de esta tabla permite identificar los modos en los que se produce una mayor variación en la frecuencia, por lo tanto, los que se pueden excitar durante los ensayos no destructivos con el fin de una fácil detección de grietas de fatiga.
Resultados de la grieta radial
De la tabla 5, se puede ver que la diferencia máxima se produce en modo 7 para el 100% del avance de grieta, con un valor de 53,77. En general se puede ver que a medida que la grieta se hace más profunda, las diferencias aumentan con respecto a los valores de la rueda sin fallo.
Otras diferencias altas se dan en el modo 10 y avance 100% (48,26), en el modo 14 y avance 100% (47,17), en el modo 11 y avance 100% (39,90), en el modo 15 y avance 100% (37,82), en el modo 17 y avance 100% (36,80), en el modo 16 y avance 100% (31,33), en el modo 8 y avance 100% (26,55), en el modo 20 y avance 100% (26,22).
Considerando los datos de la tabla 3, se representa la evolución de las frecuencias naturales de cada modo de vibración en función del avance de la grieta expresado como área de la grieta. Se definen líneas de tendencia para cada modo y se calcula los valores del coeficiente de correlación . Los valores de ofrecen la fiabilidad de las líneas de tendencias. Las pendientes de las líneas de tendencia reflejan la tendencia y la variación de las frecuencias respecto al nivel de defecto. Por ejemplo, en la figura 3 se muestra una representación de los modos 7, 14, 23, 30 y 40.
Para la selección de los ajustes más fiables, se dibujan sendos diagramas de barras representando la pendiente y el valor obtenidos para cada unos de los modos de vibración (ver Figura 4). Con el fin de diferenciar los ajustes más fiables, se establece un nivel mínimo de fiabilidad aceptable . Para la selección de las frecuencias con mayores caídas, se establece igualmente un valor mínimo de la pendiente . En base a estos criterios se observa que los modos más fiables para conocer si la rueda se encuentra fisurado o no en el caso de la grieta radial son los modos 7, 8, 9, 10, 11, 14, 15, 23, 24, 26, 27, 29, 33, 39 y 40. Sin embargo, los modos que presentan mayores caídas de frecuencias son los modos 10, 14, 15, 17,19, 21, 23, 24, 27, 29, 30, 31, 32, 39, y 40.
Combinando los dos criterios, es decir y , se obtienen los modos de mayor fiabilidad y sensibilidad a los dos tipos de defectos estudiados. Una vez excitados, se garantiza una detección eficiente de defectos. Estos modos son, en caso de la grieta radial, los modos 14, 15, 23, 27, 39 y 40 (v. Fig. 4).
Resultados de la grieta circunferencial
Del mismo modo que en el caso anterior, se procede a analizar los resultados de la grieta circunferencial. De la tabla 6, se puede ver que la diferencia máxima se produce en el modo 14 para un avance de grieta correspondiente al 50% de la circunferencia, con una caída de frecuencia del 43,348% respecto al valor inicial.
La figura 5 muestra las variaciones de las frecuencias modales de la rueda como función de las superficies de las grietas.
Igual que en el caso de la grieta radial, se puede ver que a medida que la grieta se hace más larga, las diferencias porcentuales aumentan. Otras diferencias remarcables aparecen en los modos 15, avance 50% (35,88), 7 y avance 50% (30,90), en el modo 9 y avance 50% (27,28), en el modo 21 y avance 50% (24,86), en el modo 22 y avance 50% (23,36), en el modo 29 y avance 50% (22,28), en el modo 31 y avance 50% (22,73), en el modo 30 y avance 50% (21,92) y en el modo 19 y avance 50% (21,08).
Del mismo modo que se hizo con los datos de la grieta radial, se procede a la representación de la evolución de las frecuencias naturales de cada modo de vibración en función del avance de la grieta. Se definen igualmente las líneas de tendencia para cada modo y se calculan los valores del coeficiente y los pendientes de las curvas de ajuste. Los modos más fiables son los modos 10, 12, 19, 21, 22, 23, 27, 28, 29, 30, 31, 31, 32, 33, 38 y 39. En cambio, los modos en los que se aprecian una mayor caída de frecuencias son los modos 14, 15, 19, 20, 21, 22, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 38, 39 y 40 (v. Fig. 6).
Combinando los dos criterios ( y ,), se determinan los modos a excitar para una detección eficiente de defectos. Son los modos 19, 21, 22, 27, 28, 29, 30, 31, 32, 33, 38 y 39.
Tamaño de la grieta inicial detectable mediante la metodología propuesta
Como se ha comentado anteriormente, la metodología propuesta radica en los cambios observados en el comportamiento vibratorio de la rueda debidos a la aparición de grietas de fatiga. En esta etapa de la investigación, se quiere determinar a partir de qué tamaño de grieta se aprecia una variación (disminución) en las frecuencias naturales.
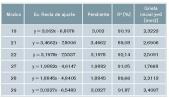
Con los datos de las tablas 5 y 6, diferencias porcentuales, se determinan las curvas de variación de las diferencias porcentuales y las rectas de ajuste de los modos eficientes para la detección de las grietas. La sección de la grieta inicial se determina calculando el punto de intersección de la recta de ajuste con el eje horizontal (). Las secciones de las grietas iniciales de los modos eficientes vienen dadas en las tablas 7 y 8, para la grieta radial y la grieta circunferencial respectivamente.
Conclusiones
En este trabajo se desarrolla y presenta una nueva metodología para la detección de grietas de fatiga en las ruedas ferroviarias, según las nuevas orientaciones técnicas descritas en el proyecto WIDEM y en la norma ASTM. En el desarrollo de este trabajo se han realizado un total de 41 análisis modales, de los cuales se ha obtenido un total de 1.640 datos de frecuencias para los dos tipos de grietas.
A tenor de los resultados obtenidos, es posible estudiar y conocer la integridad estructural de una rueda con fallo por grieta radial o circunferencial, a partir de un análisis de sus modos de vibración, comparándolos con los modos de una rueda sin defecto. Se ha demostrado que, ante fallo de fatiga, los modos vibración son perturbados y las frecuencias propias disminuyen debido a la pérdida de rigidez. Se ha logrado establecer una relación lineal entre el nivel del defecto y la frecuencia de vibración. El valor de ofrece una estimación de la fiabilidad de las funciones de las líneas de tendencia, mientras que la pendiente refleja la tendencia y variación de las frecuencias respecto al área de la grieta. Los dos parámetros permiten la selección de modos propios más sensibles y eficiente en la detección de defectos.
Agradecimientos
Los autores desean agradecer el apoyo brindado por el Gobierno español para la financiación de este trabajo a través del proyecto MAQ-STATUS DPI2015-69325-C2-1-R.
Bibliografía
Brizuela, J.D. (2010). Detección de planos en ruedas de tren por análisis ultrasónico del contacto ruedacarril en condiciones dinámicas. Tesis Doctoral en Ciencas Fisicas. Facultad de Ciencias Fisicas -Universidad Complutense de Madrid. 224p.
Brunel, J.F. (2008). Etude vibro-acoustique du crisement des roues ferroviares et de son attenuation par insertion d’elements étalliques. Thèse Doctoral en Mécanique, faculté des sciences et Technologie – Université de Lile. Lile. 94 p.
Cantini, S., Beretta, S. (2011). Structural reliability assessment of railway axles. Lucchini RS. Milano.
Carboni, M., Beretta, S. (2007). Effect of probability of detection upon the definition of inspection intervals for railway axles. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit. vol. 221, no. 3: 409-417.
Edel, K.-O., Boudnitski, G. (1997). Fracture mechanical fatigue analysis of railway wheels with rolling defects. European Structural Integrity Society 22: 125-133.
Esslinger, V., Kieselbach, R., Koller, R., Weisse,
B. (2004). The railway accident of Eschede – Technical background. Engineering Failure Analysis, 11: 515-535.
Euraxles Project. (2010). Concept and Objectives. Last view February, 2th 2017, at http://www. euraxles.eu/?page_id=6
Kalengayi, Z., Caballero, A. B., Sisamón, C. C., Alonso,
H. R., Meneses, J., Garcia-Prada, J.C. (2016). Nueva metodología para el análisis de la evolución de las frecuencias naturales con el tamaño de la grieta en ruedas ferroviarias. XXI Congreso Nacional de Ingeniería Mecánica. Elche, España, pp. 826-833.
Leadley, G.L. (1975). Overview of current efforts to detect and prevent steel wheel failures. Natl Bur Stand Spec Publ. No. 436. 22nd Meet of Mechanical Failures Preventive Group, Vol 23-25, pp 261-288.
Marin, G. L. (1995). La rupture des Roues Monobloc – L’expérience des FS. 11th International Wheelset Congress, 18-25 Juin 1995, Paris, France, Vol. 2, pp. 87-93.
Molina Sánchez, B. (2006). Estudio de la creación, desarrollo y método de detección de grietas en ruedas ferroviarias. Tesis Doctoral en Ingeniería Industrial. Escuela Técnica Superior de Ingenieros Industriales – Universidad Politécnica de Madrid, Madrid. 241 p.
Research Designs and Standards Organization. (2012). Procedure for visual & physical inspection of Wheel of ‘on’ track machines. Government of India – Ministry of railways (Report No. TM-170).
UNE-EN 13979-1:2006+A2:2011 (2011). Aplicaciones ferroviarias. Ejes montados y bogies. Ruedas monobloque. Procedimiento de aprobación técnica. Parte 1: Ruedas forjadas y laminadas. Asociación Española de Normalización, Ministerio de Energia, Turismo y Agenda Digital. Madrid.
Widem Project, D2S International. (2008). D6.1 – Development of compensated resonance inspection prototype for wheelsets.
Widem Project. (2008). Wheelset Integrated Design and Effective Maintenance. WIDEM’s Strategic Objectives. Last view May, 2th 2017, at http://www.widem.org/objectives.shtml