Conceptos y aplicaciones de la lógica borrosa

La lógica difusa o borrosa se utiliza en múltiples aplicaciones industriales, desde cámaras de vídeo al sistema de frenado de vehículos.

El primer texto conocido, en el que se trata la lógica fuzzy o lógica borrosa, aparece en 1965. Fue publicado por Lofti A. Zadeh, profesor de la Universidad de California en Berkeley. En este artículo el profesor Zadeh desarrolla la primera teoría sobre conjuntos borrosos.

Aunque sus colegas en Estados Unidos la criticaron ferozmente, fue rápidamente asimilada y aplicada a sistemas de regulación y control de dispositivos no lineales por parte de europeos y japoneses. Abe Mamdami, profesor del Queen Mary College en Londres, dio los primeros pasos tomando su relevo el grupo de trabajo del profesor Hans Zimmerman de la Universidad de Aachen (Alemania).

Aunque parezca extraño, desde el de sarrollo de la teoría hasta la aplicación de la misma en la resolución de problemas tecnológicos apenas pasaron cinco años, hecho que no ha ocurrido en la transferencia tecnológica desde la Revolución industrial.

Las primeras aplicaciones industriales se realizaron durante los años 70. El control de un generador de vapor o el de una planta cementera mediante técnicas clásicas no es trivial, puesto que los modelos matemáticos por los que se rigen estos sistemas no son lineales. En el caso del control de la cementera, éste puede ser resuelto de una forma “relativamente sencilla”, plasmando el conocimiento práctico de las personas que controlan los procesos mediante reglas que pueden ser utilizadas en lógica borrosa.

En los años 80 diferentes empresas japonesas, tales como Fuji Electric o Hitachi posteriormente, utilizan la lógica borrosa para resolver los problemas de control de una planta de tratamiento de aguas o el del control de frenado del metro de Senday respectivamente.

Toman tal auge los desarrollos de sistemas en los que se aplica la lógica borrosa que a partir de los 80 aparecen asociaciones específicamente orientadas a trabajar en este campo como SOFT (Japan Society for Fuzzy Theory and Systems) o LIFE (Laboratory for International Fuzzy Engineering Research).

Resultado de los trabajos realizados dentro del mundo de la lógica borrosa ésta es utilizada actualmente en campos tan diversos como:

1. Videocámaras y cámaras fotográ ficas.
   
2. Control de sistemas de vehículos (frenos, embragues, aire acondicionado).
   
3. Control de procesos biológicos, químicos, económicos.
   
4. Cargadores de baterías, puentes grúa.
   
5. Lavadoras, secadoras.

Es tal el número de aplicaciones en las que se está utilizando la lógica borrosa que sería imposible enumerar estas últimas o los campos en los que es o puede ser aplicada.

Bases matemáticas de la lógica borrosa: conjuntos borrosos

Normalmente la indefinición, la variación de los parámetros o la no dualidad de los problemas (blanco o negro) determinan la aparición de términos o reglas de carácter borroso “según como se mire”.

Así, ante preguntas como: ¿Qué tal día hace? es común escuchar respuestas como que hace frío o hace calor. Siendo respuestas no precisas obtenemos suficiente información de las mismas aunque no determinemos con exactitud la temperatura a la que estamos. De hecho, según en qué estación del año estemos puede variar la temperatura con la que definimos si hace frío o calor. En verano, si estamos a 16 °C decimos que hace frío, mientras que con esa misma temperatura en invierno diríamos que hace calor. Evidentemente, una persona entiende perfectamente esta respuesta ante la pregunta efectuada.

Por otra parte, los parámetros con los que son definidos los problemas suelen ser variantes con el tiempo y por tanto los modelos matemáticos en los que se fundamenta la modelización del sistema cambian y son posibles causas de fallos en los sistemas de regulación. Es decir, a la hora de diseñar un freno ABS, no se tiene en cuenta el desgaste de las ruedas que afectarán al tiempo de frenado del vehículo. Pero el sistema de control lo debe prever.

También las definiciones de ciertos sistemas pueden ser incompletas o tal su complejidad que no puede ser obtenido un modelo más o menos exacto del sistema, como por ejemplo el cuerpo humano.

Para poder definir matemáticamente conjuntos no definidos con exactitud por la teoría de conjuntos tradicional, tales como: joven, mayor, alto, bajo, fiebre alta, fiebre baja, etc., aparecen los denominados conjuntos borrosos.

Los conjuntos borrosos permiten tratar esa indeterminación, ya que un con-junto borroso no tiene el grado de radicalidad del conjunto tradicional, en el que un elemento pertenece o no al con-junto, sin casos intermedios. En el caso

de los conjuntos borrosos, se define el grado de pertenencia a un conjunto, pudiendo este variar entre 0 y 1(m_A= X [0,1]).

La interpretación de un conjunto borroso viene motivada por el acercamiento de la definición del mismo al lenguaje humano. Por ejemplo, tenemos la variable lingüística edad, acotada entre 0 y 120 años y definimos los siguientes conjuntos borrosos:

1. Personas jóvenes.
   
2. Personas adultas.
   
3. Personas ancianas.

Dados los elementos siguientes: persona de 10 años, persona de 20 años, perso na de 40 años y persona de 80 años. Según la lógica tradicional la persona de 20 años pertenecería al conjunto personas jóvenes, lo mismo que una persona de 10 años. Mediante la lógica borrosa la definición de los tres elementos podría ser la que ilustra la tabla 1.

En estas definiciones el elemento de 10 años y el de 20 años, aun perteneciendo en un grado alto al conjunto joven (1 y 0,8 respectivamente), ya son diferenciables entre sí. El grado de pertenencia al conjunto de jóvenes del de 10 años es mayor que al de 20 años, pero este último tiene un grado de pertenencia al conjunto adulto (0,1).

Representación gráfica de los conjuntos borrosos

A continuación se va a introducir la forma de representación gráfica de los conjuntos borrosos. Siguiendo con el ejemplo anterior, se tiene el dominio o universo de la variable lingüística edad, la cual varía entre 0 y 120 años, y los conjuntos que se definen en este universo son tres: joven, adulto y anciano.

En la representación gráfica (ver figura 1) se utilizan los ejes de coordenadas de manera que en el eje horizontal se distribuye el universo o dominio de la variable lingüística y en el eje vertical el grado de pertenencia del elemento o término cuyo valor varía entre 0 y 1 (m_A= X [0,1]).

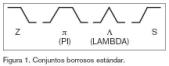
Para identificar el conjunto borroso se define una superficie, como se ve en la figura 1, representativa del universo de la edad que hace corresponder a cada edad un grado de pertenencia. Estas superficies pueden tomar variadas formas, que no tienen por qué ser lineales, ni simétricas; normalmente se utilizan cuatro distribuciones que son las denominadas funciones estándar o normalizadas y cuyas formas son las de la figura 1.

Con estas funciones y estos planteamientos iniciales en la figura 2 se pueden ver las diferentes definiciones de los conjuntos borrosos joven, adulto y anciano en el universo de la edad acotado entre 0 y 120 años. Obsérvese que se ha definido al conjunto joven con una función de tipo Z, al conjunto adulto con una función del tipo py al conjunto anciano con una función del tipo S.

Si en este momento se quiere saber la definición de una persona de 55, simple-mente se debe ir a la figura 2 y buscar a qué conjuntos pertenece y el grado de pertenencia a cada uno de ellos.

El resultado, siguiendo las líneas discontinuas, aparece en la tabla 2.

Queda entonces introducido el con-junto borroso y su representación gráfica. El conjunto borroso también se denomina función de pertenencia (m_A= X [0,1]).

Según se ha visto hasta ahora, una variable lingüística (edad) puede ser definida con varios conjuntos borrosos que abarquen todo el universo, y un elemento del universo (en este caso una persona de 55 años) se definirá por el grado de pertenencia a cada uno de los conjuntos borrosos.

Sentencias borrosas

Cumplen las funciones de las operaciones lógicas de, por ejemplo, la lógica bivalente (0,1) en las que conocidas dos variables, por ejemplo A y B la operación AND de estas dos variables da como resultado una salida, según unas reglas definidas. En lógica borrosa a partir de una sentencia de una o más variables se puede obtener una salida siguiendo las reglas que rigen las sentencias borrosas. De una manera mecánica se puede obtener el resultado de una sentencia borrosa; esto es lo que permite programar esta lógica en un microprocesador.

La forma que admiten estas sentencias es la de la lógica de predicados, y las operaciones que se pueden realizar entre los predicados son las mismas que las de la lógica de predicados. A continuación se muestran las tres operaciones más importantes, que son: disyunción, conjunción y condicional.

Disyunción

Es la función booleana O, la forma que

presenta es la siguiente:

Predicado 1 O Predicado 2

En la interpretación se pueden dar dos casos: el primero, si los conjuntos borrosos pertenecen a una sola variable, donde el resultado será el grado de pertenencia máximo de los dos grados. En el ejemplo del universo de las edades, la sentencia se representaría como se ve en la figura 3.

Gráficamente, se interpreta como la unión de las dos superficies de los dos conjuntos borrosos o funciones de pertenencia. Matemáticamente el grado de pertenencia a esta sentencia de la edad 40, se hallaría como el máximo de los grados de pertenencia a los dos conjuntos borrosos de la edad 40 años.

Grado de pertenencia de 40 años a Joven O Adulto = máximo ((0,3, joven) (1, adulto)) = 1

El segundo caso, donde los universos son diferentes, el resultado también es el mismo; es decir, el máximo de los dos grados de pertenencia. Para poner un ejemplo, se define a continuación el universo de las estaturas, en centímetros; los conjuntos que lo forman son los siguientes: pequeño, mediano, alto.

Una sentencia borrosa que relacione estos dos universos es, por ejemplo:

Joven O Mediano

El grado de pertenencia, sabiendo que el sujeto mide 190 cm y que tiene 20 años, es:

Grado de pertenencia = máximo ((0,9, Joven) (0, mediano)) = 0,9

Conjunción

Es la función booleana Y. La forma que

presentan estas sentencias borrosas es:

Predicado 1 Y Predicado 2

En esta sentencia los casos son distintos. Si los dos predicados pertenecen a distintos universos sin nada en común (por ejemplo joven y alto), o si son dos predicados dependientes con una influencia positiva de uno sobre otro (por ejemplo joven y fuerte), el resultado se obtiene como el mínimo de los dos grados de pertenencia a los dos conjuntos borrosos.

En el caso de joven y alto con el mis mo sujeto de antes de 20 años y 190 cm de altura, el grado de verdad de:

Joven Y Alto

Grado de pertenencia = mínimo ((0,9, joven) (0,3, alto) = 0,3

En el caso de que los dos predicados estén en clara contradicción, por ejemplo pequeño Y alto, el resultado se halla como el máximo de los dos grados de pertenencia, es decir, se trata como si fuera una disyunción. Como este caso es atípico y no se suele dar, como norma general de la disyunción se toma la definición del mínimo de los grados de pertenencia.

Condicional

Es la función que se define de la siguiente manera:

SI Predicado 1 Entonces Predicado 2

El resultado se halla como el grado de pertenencia mínimo, de los dos grados de pertenencia. Volviendo al mismo ejemplo del sujeto de 190 cm de altura y 20 años, el grado de pertenencia a la sentencia borrosa:

SI joven Entonces alto

Grado de pertenencia = mínimo ((0,9, joven) (0,3 alto)) = 0,3

Con estas tres operaciones se pueden formar combinaciones entre predicados para formar sentencias borrosas más complejas, cuyo resultado se calcula descomponiendo las sentencias complejas en sentencias simples; un ejemplo de esto es la sentencia:

SI el sujeto es alto Y joven Entonces saltará lejos

Para esta sentencia se ha utilizado el universo de las distancias de salto, dividido en los siguientes conjuntos borrosos: cerca, lejos. No se van a definir los conjuntos borrosos, sólo se va a ver la descomposición de la sentencia borrosa compleja en otras dos simples, que son:

SI el sujeto es alto Entonces saltará lejos.

Y

SI el sujeto es joven Entonces saltará lejos.

Grado de pertenencia = min (min ((m,alto) (m,lejos)), min ((m,joven) (m,lejos)))

En la lógica de predicados el resultado de una sentencia puede ser verdadero o falso; en el caso de la lógica borrosa, el resultado es un grado de verdad, donde la salida es la variable verdad, dividida en conjuntos borrosos; por ejemplo la salida se puede dividir en grado de certeza bajo, grado de certeza medio, grado de certeza alto; la salida es pues un grado de pertenencia a los tres conjuntos borrosos de esta variable; si la sentencia borrosa fuese falsa, la salida sería un grado de pertenencia cero a todos los conjuntos borrosos de la variable verdad. Otra forma de verlo sería mediante dos conjuntos borrosos, uno verdad, y otro falso de manera que la salida es un grado de pertenencia a estos dos conjuntos.

Proceso de implementación de un control borroso

Se va a desarrollar, a modo de ejemplo, el proceso de control de velocidad de un motor de corriente continua mediante lógica borrosa.

Introducción de las variables

Se introducen en el programa las variables de entrada: error de velocidad y corriente (borrosificación), y salida acción (deborrosificación) y se definen los términos de cada una de ellas, inicialmente la definición de éstos se hace de manera intuitiva.

El error_velocidad es definido mediante cinco términos lingüísticos o conjuntos borrosos que son: muy_lento, lento, bueno, rápido, muy_rápido

La corriente, por ser variable secundaria, se define mediante tres términos lingüísticos o conjuntos borrosos que son: corriente positiva alta (pos_alta), co rriente buena (buena) y corriente negativa alta (neg_alta).

Corriente buena significa que está dentro de un rango válido, y corriente (neg_alta) o (pos_alta) que están fuera de rango (figura 5).

Por último, definimos la variable acción, que es la salida del regulador. Esta, al ser la de salida del regulador, se implementa mediante cinco términos lingüísticos o conjuntos borrosos que son (figura 6):

acelera_fuerte,

acelera, sin_acción,

frena, frena_fuerte

Cuyos significados son: acelera fuerte realiza una acción que conlleva una aceleración brusca; acelera que equivale a una aceleración suave, sin acción que equivale a no actuar sobre la velocidad del motor, frena que equivale a una acción de deceleración suave y frena fuerte que equivale a una acción de deceleración brusca.

Sobre el eje de abscisas aparece el valor analógico que tiene la variable real o universo del discurso; por ejemplo, la corriente en amperios. Ésta es una facilidad que permite un manejo más intuitivo de las variables, que si se tuviera que trabajar con datos digitales, que son más difíciles de interpretar de cara al ajuste del regulador de una manera intuitiva.

Sobre el eje de ordenadas aparece µo grado de pertenencia de un cierto valor real a cada uno de los conjuntos borrosos o términos de los que consta una variable lingüística.

Introducción del bloque de reglas

Una vez definidas las variables y sus conjuntos borrosos, se pasa a definir el bloque de reglas que va a gobernar el sistema (inferencia). Éstas son las que aparecen en la tabla 3.

Con estas siete reglas queda perfectamente definido el regulador (tabla 3); en ellas entran todas las variables y todos los conjuntos borrosos necesarios y han que-dado contemplados todos los casos que se pueden dar y que son físicamente posibles.

Los resultados borrosos obtenidos de estas reglas se aplican sobre la matriz de inferencia de la variable de salida (acción) que posteriormente se convierte en una variable real (tabla 4).

Conclusión

La lógica borrosa, lógica difusa o fuzzy logic es una técnica relativamente novedosa que nos permite describir el comportamiento de los sistemas mediante reglas, utilizando un lenguaje coloquial

1. o natural, el cual tiene propiedades tales como: la imprecisión o la vaguedad de los términos, propiedades que están en absoluta oposición con la lógica clásica
   
2. o proposicional.

La lógica borrosa une los métodos clásicos de diseño de sistemas de control junto con el conocimiento de los expertos, evitándose así la necesidad de conseguir modelos matemáticos rigurosos del comportamiento de los sistemas.

Una de las grandes diferencias con otros sistemas de control es que, aunque la lógica borrosa se apoya en un complejo cuerpo matemático, la aplicación de la misma es muy sencilla y esto la hace muy interesante.

Pero, cuidado; no confundamos la lógica borrosa como un método mágico que nos vaya a resolver todos los problemas de control. Muchas veces los sistemas clásicos son mejores, más eficientes y más baratos para resolver el mismo problema.

Con este artículo se ha pretendido dar a conocer las bases de una técnica de control no basada en la lógica proposicional clásica. Siendo una técnica muy ampliamente utilizada en sistemas de control, es la gran desconocida.

Bibliografía

Martín del Brío, B. y Sanz Molina, A (1997). Redes neuronales y sistemas borrosos. Ed. RA-MA.

Hanss, Michael (2005). Applied fuzzy arithmetic: an introduction with engineering applications. Ed. Springer.

Mendel, J. M. (1995). Fuzzy Logic Systems for Engineering: A Tutorial, Proceedings of the IEEE, vol. 83, pp. 345-377.

Takagi, H y Sugeno, M. F. (1985). Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. on Systems, Man, and Cybern., SMC-15(1). pp. 116-132.

Terano, T., Asai, K. y Sugeno, M (1992). Fuzzy Systems Theory. Ed. Academic Press Inc.

Trillas, E. y otros (1994). Fundamentos e introducción a la ingeniería Fuzzy. Omron Electronics S.A.

Zadeh, L.A (1965). Fuzzy Sets. Information and Control, Vol 8, pp. 338-353.

Japan Society for Fuzzy Theory and intelligent informatics- http://www.j-soft.org/index-e.html.

The European Society for Fuzzy Logic and Technology (EUSFLAT) -http://www.eusflat.org/

International Fuzzy Systems Association – http:// www.cmplx.cse.nagoya-u.ac.jp/~ifsa/