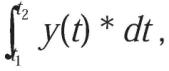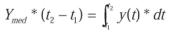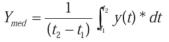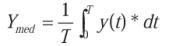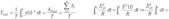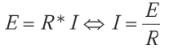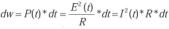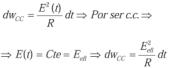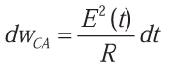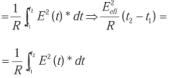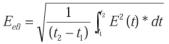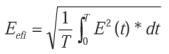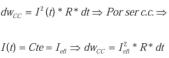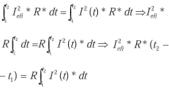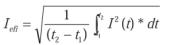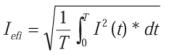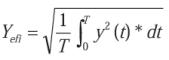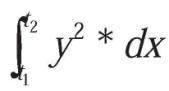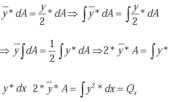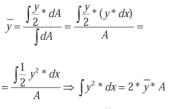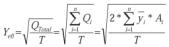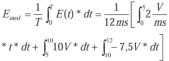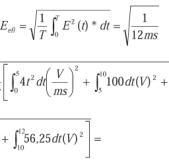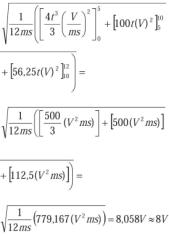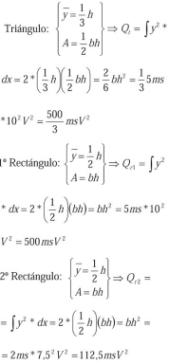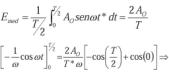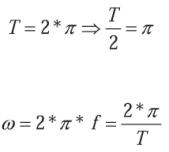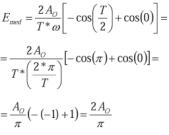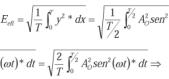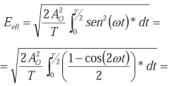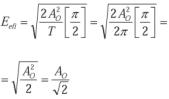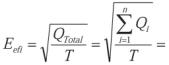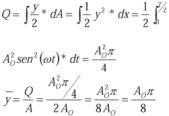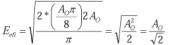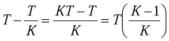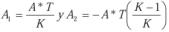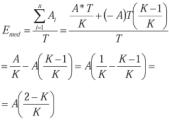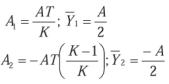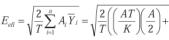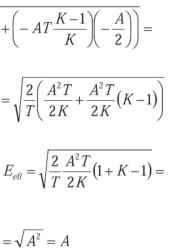Cálculo simplificado del valor medio y eficaz de una forma de onda
Propuesta de una alternativa para facilitar los cálculos en las formas de onda generadas en diferentes máquinas y dispositivos eléctricos
Introducción
Dentro del campo de la Tecnología Eléctrica, la determinación del valor medio y eficaz de las formas de onda generadas en las distintas máquinas eléctricas, onduladores y demás dispositivos, es fundamental para el cálculo de potencias y rendimientos de los mismos. Desde el punto de vista didáctico, el cálculo de estos valores por los métodos matemáticos de integración es lo habitual, representando para los alumnos el uso excesivo de tiempo por la complejidad de los mismos, así como una fuente de errores por los mismos motivos. Desde este artículo se expone una alternativa que puede facilitar enormemente el cálculo de estos valores, siempre que las ondas a estudiar lo permitan, reduciendo el cálculo, y permitiéndonos centrarnos en otros aspectos de los problemas a estudiar.
Teoría
Valor medio
Se define el valor medio de una forma de onda o señal como la media de todos los valores que definen dicha onda. La suma de todos los valores de la onda es el área encerrada bajo la curva entre dos puntos dados y la calcularemos como:
este valor ha de ser igual al área de un rectángulo de base los dos puntos dados y de altura el valor medio. Por consiguiente, igualando las dos áreas:
Despejando el valor medio:
Si la forma de onda es periódica se suele tomar como intervalo de integración el del 1.º período con lo que: t1 = 0 y t2 = T, quedando la expresión:
Este intervalo es suficiente, ya que si tomamos n períodos aumentamos en n el tiempo, pero también aumentamos en n el área con lo cual obtenemos el mismo resultado.
El cálculo se puede simplificar si la forma de onda o señal se puede descomponer en una serie de superficies regula-res, de manera que:
Donde Ai es cada una de las áreas regulares de esas superficies en las que se puede descomponer la forma de onda.
Valor eficaz, efectivo o RMS (Root Mean Square – raíz media cuadrática)
Es el valor equivalente de una fuente de corriente continua que produciría la misma cantidad de calor o energía (también podemos considerar potencia, dado que es por el mismo tiempo) sobre el ciclo completo de una señal dependiente del tiempo. En definitiva:
El valor RMS o valor eficaz es el valor del voltaje o corriente alterna que produce el mismo efecto de disipación de calor que su equivalente de voltaje o corriente, en corriente continua sobre una misma resistencia.
De esta definición podemos obtener la expresión para calcular el valor eficaz. La energía disipada en una resistencia de valor R ohmios es:
dw = P(t) * dt
Donde P(t) es la potencia instantánea.
La potencia la podemos expresar en función de la tensión (E) o la intensidad (I), ya que estas dos variables son linealmente dependientes con constante de proporcionalidad R:
En definitiva la energía disipada en forma de calor se puede expresar como:
Deduciremos el valor eficaz, primeramente, utilizando la tensión y posteriormente mediante la intensidad:
1.º Caso: Tensión
Energía en la resistencia en c.c.:
El subíndice efi es por la propia definición de valor eficaz.
Energía en la resistencia en c.a.:
Igualamos las dos expresiones e integramos a lo largo de un intervalo:
Simplificando el valor de R (es el mismo valor resistivo) y despejando el valor eficaz:
Si la integración se realiza a lo largo de un período por ser una forma de onda periódica tendremos (t1 = 0 y t2 = T):
1.º Caso: Intensidad
Energía en la resistencia en c.c.:
El subíndice efi es por la propia definición de valor eficaz.
Energía en la resistencia en c.a.:
dwCA = I2(t) * R * dt
Igualamos las dos expresiones e integramos a lo largo de un intervalo:
Simplificando el valor de R (es el mismo valor resistivo) y despejando el valor eficaz:
Si la integración se realiza a lo largo de un período por ser una forma de onda periódica tendremos (t1 = 0 y t2 = T):
Conclusión: En general para cualquier función dependiente del tiempo (y(t)) y que sea periódica, su valor eficaz se calculará:
Cálculo del valor eficaz mediante el momento de la figura
En el valor eficaz aparece la integral:
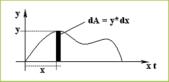
expresión que se corresponde con el momento estático o de primer orden de una figura plana, con respecto al eje x (figura 1). Si la forma de onda se puede descomponer en figuras o superficies más comunes, el cálculo del valor eficaz se puede realizar a partir de sus momentos estáticos.
Si no conocemos los momentos estáticos, una forma rápida de calcularlos es teniendo en cuenta el centroide ( y ) de las figuras planas que normalmente sí son conocidos:
quedando la expresión:
Donde Qi es el momento estático de cada una de las figuras regulares en las que se puede descomponer la función o forma de onda en cuestión e y1es el centroide de cada una de las figuras, junto con Ai que es el área de las figuras regulares. Este producto siempre es positivo, dado que si el área es negativa, el centroide también lo será, con lo cual, su producto es positivo como se ha dicho.
Resultados
1.º) Ejemplo de aplicación
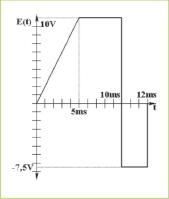
Determinar el valor medio y el valor eficaz de la siguiente forma de onda, en el intervalo indicado:
Solución:
Empezaremos calculando el valor medio de la forma de onda. Como no es una onda continua, la tendremos que definir a intervalos:
a) Método de integración:
Integrando y sustituyendo:
El valor medio es:
Emed = 5V
b) Método de las áreas:
La forma de onda se puede descomponer en tres áreas regulares de fácil cálculo: un triángulo y dos rectángulos.
a) El valor eficaz se calcula por integración como:
b) Método del momento de primer orden o momento estático:
Los momentos estáticos de las áreas que componen la forma de onda son los siguientes:
El momento estático total será:
QT = Qt + Qr1 + Qr2 = (500/3) + 500 + (225/2) = (4675/6)msV2
El resultado obtenido es:
Ejemplo de aplicación
Determinar el valor medio y el valor eficaz de un semiperíodo de una señal alterna senoidal.
Solución
a) Método de integración:
Si tenemos en cuenta que:
Sustituyendo valores:
b) Método de las áreas: Calcularemos el área del semiciclo:
falta ecuación 1
a) El valor eficaz de la señal senoidal por el método de integración es:
b) Método del momento de primer orden o momento estático:
falta ecuación 2
Necesitamos conocer el centroide del semiciclo senoidal:
Y por consiguiente:
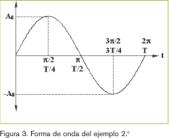
Ejemplo de aplicación
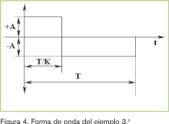
Determinar el valor medio y el valor eficaz de la siguiente forma de onda, en el intervalo indicado:
Solución
a) El valor medio por integración es:
b) El valor medio por el método de las áreas es:
El 1º semiperíodo tiene por duración: T/K y el 2º semiperíodo será:
Si tenemos en cuenta que las áreas de la forma de onda son de geometría cono cida, podremos determinar que:
El valor medio se puede calcular cuando las áreas son conocidas, como:
a) El valor eficaz por integración es:
b) El valor eficaz por el método de los momentos es:
Utilizando el método del momento estático o de primer orden, tendríamos:
Conclusiones
Como se desprende del presente artículo, el cálculo del valor eficaz de una forma de onda, de la cual se conoce su centroide, es sumamente más simple que el cálculo tradicional por integración, siendo necesarias menos operaciones y por consiguiente con menor posibilidad de error. Si las formas de onda complejas se pueden descomponer en otras más simples, el cálculo se reduce al utilizar una tabla que nos defina los centroides de las figuras simples más utilizadas o comunes. Este método permite abordar métodos numéricos simplificados para la determinación del valor medio y eficaz de una forma de onda.
Agradecimientos
A Marcelino Zazo Rodríguez y a D. José María Bernaldo de Quirós Sánchez, por sus inestimables aportaciones y correcciones a este artículo.
Bibliografía
Mecánica Técnica – W. G. McLean – McGraw-Hill
Cálculo Diferencial e Integral – Frank Ayres, JR. -McGraw-Hill
Circuitos Eléctricos – Joseph A. Edminister – McGraw-Hill
RESUMEN
En el presente artículo se expone el cálculo del valor medio y eficaz (valor cuadrático medio) de una forma de onda por el método tradicional de integración y por los métodos de áreas y momentos. Para ello, se realiza una revisión de estos conceptos y se aborda una forma simplificada del cálculo de dichos valores cuando se conoce el momento de primer orden, momento estático o centroide de las figuras que forman la onda en cuestión, valores que se pueden consultar en cualquier tabla de áreas, centroides, momentos estáticos y de inercia de Mecánica. Final-mente, se exponen tres ejemplos de aplicación del cálculo del valor medio y eficaz por los dos métodos.