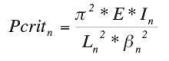Cálculo de la longitud de pandeo en pórticos

 

Para los ingenieros calculistas de estructuras, en este artículo se analiza el problema del cálculo de la longitud de pandeo en pórticos ortogonales y se propone un método para simplificar el proceso

La normativa española NBE-EA-95 y el Eurocódigo 3 (método incluido en el anexo E) incluyen tablas y nomogramas para la determinación del coeficiente de pandeo ß (el =ß*l) con el que se determina la longitud eficaz de pandeo de una columna de un entramado traslacional.

Ambos códigos proporcionan enfoques similares en el cálculo de la longitud eficaz de pandeo para miembros en compresión, la norma NBE-EA-95 está basada en los estudios de Julian y Lawrence¹ (1959) mientras que el procedimiento del Eurocódigo 3 se debe a los trabajos desarrollados por Wood² (1974) con resultados muy similares a los aportados por la ecuación trascendente propuesta por Julian y Lawrence.

En los casos referenciados de pórticos metálicos traslacionales articulados en la base, ambos códigos proporcionan similares resultados con errores que en algunos casos, donde no se cumplen las hipótesis con las cuales se han desarrollado los métodos indicados, pueden conducir a diseños del lado de la inseguridad.

Mediante el procedimiento presentado se propone modificar las longitudes de pandeo de forma que el factor de seguridad al pandeo en los pisos superiores sea consistente con el factor de seguridad de la columna de referencia (piso inferior).

Aunque el comportamiento real de los entramados metálicos es más complejo y las columnas de los pisos superiores transferirán parte de su rigidez para incrementar el coeficiente de seguridad al pandeo de los pisos inferiores, el procedimiento presentado es conservador.

Se han incluido una serie de ejemplos en los que claramente se muestra la ventaja de este método en contra del enfoque tradicional. La validación del mismo se realiza con los resultados obtenidos mediante un programa de elementos finitos con el módulo de pandeo global elástico.

El nomograma

Los nomogramas desarrollados por Julian/Lawrence y Wood están basados en el pandeo de un entramado reducido consistente en la columna en investigación y los elementos inmediatamente adyacentes (columna superior, inferior, vigas que acometen a la columna arriba y abajo). La ecuación trascendente que se obtiene como resultado de la solución de pandeo se representa gráficamente en el nomograma para pórticos traslacionales (la norma NBE-EA-95 apartado 3.2.4.4 incluye una fórmula aproximada en lugar del nomograma de Julian y Lawrence).

El nomograma está ampliamente aceptado como método para obtener los factores ß de pandeo que se utilizarán en el diseño de columnas. Sin embargo la obtención de este nomograma ha implicado una serie de hipótesis y simplificaciones las cuales si no se cumplen en la estructura en investigación pueden arrojar resultados imprecisos dando lugar a diseños inseguros.

Las hipótesis de partida para el desarrollo de los nomogramas son las siguientes:

1. El comportamiento del entramado es elástico.
   
2. 2. Todos los nudos son rígidos.
   
3. Todos los elementos son prismáticos de sección constante.
   
4. Todas las columnas del entramado pandean simultáneamente.
   
5. Las vigas carecen de fuerzas de compresión.
   
6. El parámetro de rigidez F= L debe ser igual para todas las columnas.
   
7. El grado de restricción en los nudos se distribuye en la columna superior e inferior al nudo en proporción a la rigidez de las dos columnas.
   
8. La rotación en los extremos de los elementos restringidos son iguales en magnitud y opuestos en signo para pórticos traslacionales, produciendo curvatura inversa.

Estas hipótesis están basadas en condiciones idealizadas, raramente existente en la práctica, el nomograma es aplicable a pórticos con simetría en cargas y geometría y proporciona buenos resultados cuando la rigidez es proporcional a las cargas.

Se han elaborado varios trabajos presentando alternativas al método del nomograma en aquellos casos en los cuales los resultados no son realistas, estos trabajos han sido desarrollados mayor-mente en Estados Unidos en cuyo código AISC tanto en la versión ASD (Diseño en tensiones admisibles) como en el LRFD (Diseño en estados límites) se presenta el nomograma de Julian y Lawrence como método de cálculo del factor de longitud efectiva.

Métodos de cálculo del factor de longitud efectiva ß

Seguidamente se exponen algunos de los métodos alternativos presentados en la literatura técnica para el cálculo del factor de longitud efectiva ß.

Método de LeMessurier³

Método más preciso que utilizando el nomograma, este método tiene en cuenta la restricción lateral ejercida entre columnas.

Las columnas en un nivel considerado pandearán simultáneamente, la columna mas rígida o la columna con poca carga de compresión arriostrará contra pandeo la columna menos rígida o la que tenga una mayor carga de compresión.

El factor de longitud efectiva (ß) de la columna ‘i’ será:

Método de Lui⁴

Este método tiene en cuenta tanto la inestabilidad de la columna (P-d), como la inestabilidad del pórtico (P-?). La fórmula propuesta es simple y necesita sola-mente de un análisis de primer orden, asimismo tampoco necesita acudir al nomograma u otros gráficos.

Método de Puwein-Sahmel⁵

El método se basa en la similitud de las deformaciones que se producen en un pórtico, cuando se excede la carga de pandeo en una pequeña cantidad y la que produce una carga horizontal unitaria en el dintel.

Una descripción y ejemplos de este método pueden encontrarse en la referencia⁶ indicada en la bibliografía.

Método de Pandeo Global Elástico

Es el método más exacto de todos los métodos de cálculo de factores de longitud de pandeo.

Los factores ß se obtienen tras el cálculo de la carga crítica de pandeo Pcrit = Crit. * P, e igualando esta carga crítica a la carga de pandeo de Euler.

La determinación del coeficiente crítico Crit. Se realiza con la ayuda del cálculo matricial.

El método indicado se detalla en la referencia⁷.

Este método tiene la gran ventaja de la versatilidad no estando limitado por las complejidades de geometría de los entramados ni por las condiciones de contorno.

Existen en el mercado numerosos programas de ordenador que incluyen módulos de cálculo de pandeo elástico. En la bibliografía se incluyen algunos de ellos^8,9, cabe destacar en este aspecto el libro presentado por el profesor R. Argüelles indicado en la referencia¹⁰, que sin duda recomiendan el autor como referencia obligada.

Cálculo de los factores ß por el método de las asimetrías

Los pórticos traslacionales articulados en la cimentación se utilizan con asiduidad en los diseños estructurales industriales y de edificación.

Las longitudes de pandeo de las columnas del pórtico se modificarán de forma que el factor de seguridad al pandeo en los pisos superiores sea consistente con el factor de seguridad de la columna de referencia con unión a la cimentación.

El método tiene en cuenta asimetrías de cargas y de inercias, siendo aplicable incluso a pórticos de una sola altura. El método presentado ha sido tratado en la referencia¹¹, en la cual se presenta el método con factores de corrección preliminares para la columna de referencia.

El autor ha modificado este método excluyendo la consideración de estas correcciones, las cuales tienen escasa influencia en el resultado final, teniendo en cuenta la comparación con el método de pandeo global que se considera como exacto.

Tal y como se observará de los ejemplos presentados el método es fácilmente codificable en hojas de cálculo y lenguajes de programación.

El método es de aplicación directa en los cálculos de pórticos donde todavía hoy en día la mayoría de los programas de cálculo carecen de módulos de pandeo lineal.

Las mayores diferencias encontradas entre el nomograma y el cálculo con pandeo global se encuentran en pórticos traslacionales con uniones articuladas a la cimentación, para estos casos la aproximación con el método propuesto justifica ampliamente su consideración a la hora de definir los coeficientes ßde pandeo.

No se incluyen en este artículo consideraciones de tipo anelástico, ya que si se utilizan los nomogramas para determinar los factores ß, implícitamente se asume que se realizará bajo un pandeo elástico del sistema.

El método se aplica a pórticos planos donde no se analiza el pandeo en el plano normal al del pórtico. En un diseño final el análisis del pandeo en ambos planos debe tenerse en cuenta.

Figura 1. Variación de los coeficientes ßpara pórticos de una altura y diferentes cargas de comprensión.

Procedimiento de cálculo

El procedimiento de cálculo requiere los siguientes pasos mínimos:

1. Datos iniciales: Dimensiones geométricas del entramado, momentos de inercia de las barras y cargas de compresión en las columnas. Todo en un sistema consistente de unidades.
   
2. Cálculo de los factores ßpara las columnas conforme a los códigos NBEEA-95 y Eurocódigo 3.
   
3. Cálculo de la carga de pandeo de Euler para todas las columnas del modelo.
   

4. Cálculo del factor de carga (LF) asociado a cada columna.

5. Selección del coeficiente crítico de pandeo:

   Ccrit =Min (LF _{column 1} ….LF_columnn)

   La columna asociada con este coeficiente crítico se denominará columna de referencia.
   

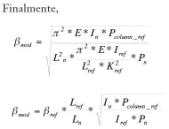
6. Cálculo del coeficiente ßmodificado para cada columna, aplicando la ecuación de pandeo de Euler y teniendo en consideración el coeficiente crítico determinado en el punto anterior:
   

En el gráfico de la figura 1, extraído de la referencia¹⁶, se comparan los resultados de cuatro de los procedimientos indicados en un pórtico de una altura, variando una de las cargas y para diferentes valores del coeficiente G = (Ic/Lc)/(Ib/Lb). Se observa la buena correlación del método de las asimetrías, comparado con el método de Lui y Lemessurier.

Seguidamente se incluyen varios ejemplos donde pueden apreciarse la aplicación del método expuesto y su comparación con los resultados ofrecidos por el programa de elementos finitos Marc Designer⁶ a través de su módulo de pandeo lineal.

El cálculo de la longitud de pandeo de pórticos ortogonales metálicos conforme a la normativa NBE-EA-95 y Eurocódigo 3 puede conducir a diseños inseguros, si no se cumplen las hipótesis de partida para la aplicación de los procedimientos incluidos en los códigos citados. En este artículo se incluye un método para calcular las longitudes de pandeo de las restantes barras del pórtico, basándose en la longitud de pandeo de la columna más cargada. El método propuesto se ilustra con ejemplos y se comparan los resultados obtenidos con la aplicación de la normativa existente y con el cálculo mediante un reconocido programa de elementos finitos que realiza análisis de pandeo global elástico.

Ejemplos

Ejemplo 1 (NBE-EA-95)

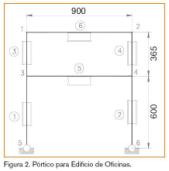
Pórtico para edificio de oficinas.

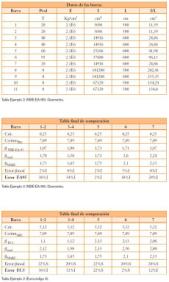
De este ejemplo se observa que el error, obtenido de la comparación con el cálculo matricial, en el factor (de la aplicación de la norma EA95 es un 74% del lado de la inseguridad frente a un error del 16% (del lado de la seguridad) del método propuesto.

Las diferencias tan apreciables con el cálculo tradicional se desprenden de dos factores ponderantes:

1. En el método matricial se analiza el pandeo global del pórtico. El método de Julian y Lawrence sólo tiene en cuenta el pandeo de un entramado reducido.

2. La diferencia de longitudes en las columnas 1-2 y 3-4 produce una solución no conservadora en el método utilizado por la NBE-EA-95. Esto es debido a que las columnas más cortas se hacen más rígidas a pandeo y las más largas se “apoyan” de éstas incrementando el factor ß de las columnas cortas.

Tabla Ejemplo 1 (NBE-EA-95). Geometría.

Figura 2. Pórtico para Edificio de Oficinas.

Existe por tanto una transferencia de rigidez de las columnas cortas a las inferiores para aumentar su resistencia a pandeo.

Aquí se observa un ejemplo donde factores ß elevados es significado de elementos de elevada rigidez en completa oposición al concepto tradicional.

Ejemplo 1 (Eurocódigo 3)

Cálculo de los factores ß según Eurocódigo 3.

Columna 1 y 2.

GA = 1; articulado en la cimentación.

Ic

GB = ^{? Lc} = ^{75,4 + 63,4} = 0,626

_? Ig _{+ ?} Ic 82,9 + 75,4 + 63,4 Lg Lc

Del nomograma del Eurocódigo 3 (traslacional): ß1 = ß2 = 2,83

Columnas 3 y 4.

GA == = 0,626

GB = == 0,74

Del nomograma del Eurocódigo 3 (traslacional): ß1 = ß2 = 1,90

El Eurocódigo 3 nos da errores conservadores de un 27% comparado con el resultado del cálculo matricial en las columnas 1-2 y errores del lado de la inseguridad del 70% en las columnas 3-4.

El método de las asimetrías nos da un error del 24% del lado de la seguridad.

Ejemplo 2 NBE-EA-95

Pórtico para edifico industrial.

1. Geometría.

Ejemplo 2 Eurocódigo 3

En este ejemplo se ha incluido una variación en las cargas e inercias, incumpliendo de esta forma la hipótesis del nomograma con el parámetro L*(P/I) ^0,5 idéntico para todas las columnas del mismo nivel, el método propuesto determina un factor ß (caso de la norma EA95) con una buena aproximación al valor determinado con el cálculo por pandeo global (< 5%).

Por otro lado, se observa que el EC3 da errores superiores en el factor ß modificado (aunque siempre conservadores) ya que el coeficiente crítico es menor en el EC3.

Conclusiones

El método de las asimetrías ofrece una aproximación conservadora para determinar los factores ß, corregidos de los calculados con los nomogramas propuestos por la normativa vigente.

En general el EC3 da unos valores más conservadores de los factores ß que la norma NBE-EA-95.

Para un cálculo más exacto se recomienda la aplicación de los métodos de pandeo global elástico debido a su aplicación a problemas complejos, sin limitaciones geométricas, de cargas, enlaces de barras y condiciones de contorno.

Como comentario final, indicar que los calculistas de estructuras deben reconocer que los modelos simplificados, para columnas aisladas y entramados reducidos no representan el comportamiento real del pandeo de pórticos y su visión tradicional de facto-res de pandeo, longitudes efectivas de pandeo y en algunos casos incluso la esbeltez de las barras (caso de discretización de una barra en múltiples elementos) debe cambiar.

Bibliografía

1. 1. Julian, O.G. , Lawrence, L.S. “Notes on J. and L. Nomograms for Determination of Effective Lengths”, 1959
   
2. Wood, R.H., Roberts, E.H. “A Graphical Method of Preventing Sidesway in the Design of Multi-Storey Buildings”, Proceedings of institution of Civil Engineer. London. 1975
   
3. LeMessurier, W.J., “A Practical Method of Second Order Analysis, Part 2-Rigid Frames” AISC Engineering Journal 2nd Qtr., 1977
   
4. Lui, E.M. “A Novel Approach for K Factor Determination” AISC Engineering Journal 4^th Qtr. 1992
   
5. Paul Sahmel, Duisburg-Neudorf, Der Stahlbau April 1955
   
6. Prontuario de Ensidesa, Tomo II* 1ªEd. 1977. Pág 207-209
   
7. Halldorsson, O.P. and Wang, C.K. “Stability Analysis of Frameworks by Matrix Methods” ASCE Journal of the Structural Division. Vol 94 July 1968
   
8. MARC Analysis Research Corporation-Europe. 2715CA Zoetermeer, The Netherlands. MARC Designer Software
   
9. Robot 97. RoboBAT . 25, Avenue du Garnier 38240. Meylan Zirst. France
   
10. Argüelles Álvarez R. y Argüelles Bustillo R. Análisis de Estructuras. Fundación Conde del Valle de Salazar. 1996
    
11. C.V.G. Siderurgica del Orinoco (Sidor) Manual de Proyectos de Estructuras de Acero. 1982
    
12. NBE-EA-95 . Estructuras de Acero en la Edificación. Ministerio de Fomento. Madrid 1998
    
13. CEN (1993) ENV 1993-1-1 Eurocode 3, Design of Steel Structures, European Committee for Standardization, Brussels.
    
14. American Institute of Steel Construction. “Specification for Structural Steel Buildings – Allowable Stress Design”. Chicago IL 1989
    
15. American Institute of Steel Construction, Load and Resistance Factor Design Specification for Steel Buildings, Chicago IL 1993
    
16. Shanmugam, N.E., Chen,W.F. “An Assessment of K Factor Formulas”, AISC Engineering Journal , First Quarter, 1995
    
17. Alarcón Alvarez y otros. “Cálculo de Estructuras”. Ed.Reverté, S.A. Barcelona 1986
    
18. Belluzzi, O, “Ciencia de la Construcción” (4 Tomos). Aguilar. Madrid 1967.