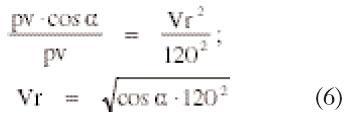Cálculo de apoyos en zona A para líneas aéreas de alta tensión
El autor propone reconsiderar los cálculos para los apoyos en ángulo y especiales de líneas aéreas de alta tensión en zona A, con altitudes de 0 a 500 metros
La isla de Tenerife es un buen taller de prácticas para proyectistas de líneas aéreas de A.T., ya que, con buena suerte, o no tan buena, te pueden encargar un proyecto que, en un trazado de 3 km atraviese las 3 zonas, A, B y C, pero, zonas que son muy peculiares: la zona A de la costa sur, siempre seca y soleada, tiene poco que ver con la zona A de la costa norte, a veces húmeda y salitrosa debido al “mar de nubes”, popularmente llamada: “panza burro”. Cuando asciendas a los 1000 metros, donde reglamentariamente tendrás que considerar hielo de zona C, ¡qué va!, éste no lo encontrarás hasta que subas otros 1000 aproximadamente, es decir, cuando estés a media altura entre el mar y la cumbre del omnipresente Teide. De alguna manera, el germen de la idea que desarrollo aquí pudo tener su origen en las conversaciones que mantuve con colegas de esa “Isla Afortunada”. A todos ellos les dedico este trabajo.
Apoyo de ángulo en zona A
La forma convencional de abordar este cálculo es considerar que el esfuerzo total transmitido al apoyo es la suma de la resultante de las tensiones de los conductores de los vanos adyacentes, más las proyecciones sobre esa resultante de los esfuerzos provocados por la presión del viento sobre los dos semivanos.
Resultante de las tensiones
Si las tensiones en el conductor son iguales a los dos lados del apoyo, que es lo normal, no hay desequilibrio, y su resultante coincidirá con la bisectriz del ángulo. En estas condiciones dicha resultante rT para un conductor vale:
rT = 2Tm × sen a (1)
Tm = tensión máxima del conductor a ambos lados del apoyo
a = mitad del ángulo (2a) de desviación de la traza de la línea
Resultante de la presión de viento
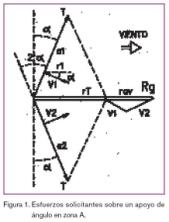
Se supone que la dirección del viento es la misma que la de la resultante rT (figura 1).
La fuerza originada por la presión del viento sobre el vano a1 es perpendicular a éste y por lo tanto forma un ángulo a con la dirección del viento. El apoyo recibe la presión de medio vano y la fuerza vale:
v1 = 0,5 a1 × pv × cos a (2) pv = presión de viento por metro
La proyección de esa fuerza sobre la resultante de las tensiones, en este caso la bisectriz, vale:
r1 = v1 × cos a y sustituyendo v1 por su valor en (2)
r1 = 0,5 a1 × pv × cos2 a (3)
Lo mismo ocurre con el vano a2
Teniendo en cuenta que la suma de los semivanos es el vano de viento
av = 0,5(a1 + a2)
La resultante de la presión de viento será:
rav = av × pv × cos2 a (4)
La resultante total de esfuerzos sobre el apoyo de ángulo con viento será:
Rg = 2T × sen a + av × pv × cos2 a (5)
En esta fórmula (5), sobre el sumando de viento (2º término), nada que objetar. En cuanto al sumando de tensiones parece necesario reconsiderarlo ya que la tensión máxima sólo se produce cuando la dirección del viento es perpendicular al vano y su velocidad es de 120 km/h. Cuando la dirección del viento y la transversal al vano forman un ángulo a, la presión de viento sobre medio vano es la de la fórmula (2) y la tensión del conductor en ese vano será menor que la tensión máxima.
Como la presión del viento sobre el conductor es directamente proporcional al cuadrado de la velocidad de ese viento; vamos a calcular qué velocidad reducida Vr correspondería a un viento que, actuando transversalmente sobre el vano a1, produjera el mismo efecto que un viento de 120 km/hora sobre ese vano desviado un ángulo a de la transversal. Proponemos la siguiente relación:

Ejemplo: conductor LA 56, tensión de rotura Tr = 1641 daN, tensión máxima de trabajo Tm = 520 daN (Cs = 3,15), presión del viento a 120 km/h, pv = 0,556 daN/m.
vanos: a1 =160 m; a2 = 140 m; av =150 m.
Con estos datos realizamos la tabla 1 para ángulos: a = 0 a 45º, que ilustramos con la figura 1.
Para una desviación de la traza de 90º (a = 45º), el esfuerzo solicitante para 3 conductores será:
Fórm. 5 para T´ reducida; Rg = 3 × 645,7 = 1.937 daN. Apoyo: C 2000 Fórm. 5 para T = 520 (const.); Rgk = 3 × 777,1 = 2.331. Apoyo: C 3000
Apoyo de derivación
El artículo 30.3 del RLAT dice: “En el caso de apoyos especiales se considerarán las distintas acciones definidas en los artículos 15 a 20, que pueden corresponderles de acuerdo con su función, combinadas en unas hipótesis acordes con las pautas generales seguidas en el establecimiento de las hipótesis nor-males”.
¿Nos permite este párrafo sumar car-gas de desequilibrio de la 3ª hipótesis (anormal), a otras hipótesis, especial-mente en caso de proyectos en los que esta 3ª debamos considerarla como normal para poder eludir la 4ª hipótesis (art. 30.3.b)? Creemos que sí, y así lo interpretaremos en el estudio del apoyo de derivación.
Derivación tensada en apoyo de alineación o de anclaje
En el cálculo de una derivación sobre apoyo de alineación o anclaje en zona A, teniendo en cuenta que, según hemos visto anteriormente, la tensión en un vano queda reducida si el viento no es transversal, resultará que en un apoyo de derivación habrá que buscar la dirección del viento que hace más desfavorable la carga total solicitante sobre todo el con-junto.
Supongamos un apoyo de alineación con los mismos datos de cable y vanos que la figura 1, con una derivación perpendicular del mismo cable y 145 m de vano. Si la dirección del viento es transversal a la línea de origen (paralelo a la derivación), tenemos que en la derivación, la presión de viento es cero, y la tensión T´ en ella pasa de valer 520 daN a 241,1 daN. La presión de viento sobre el vano de viento av es 83,4 daN cuando es paralelo a la derivación y cero si es transversal. La presión del viento sobre la derivación es cero en el primer caso y 40,3 daN en el segundo. En resumen, que la carga total será:
Viento paralelo a la derivación
Rgp = 83,4 + 241,1 = 324,5 daN
Viento transversal a la derivación:
Rgt = v(40,3 + 520,0) = 521,7 daN (son vectores perpendiculares)
De lo anterior se deduce que la dirección más desfavorable del viento, en términos generales, será la transversal a la derivación, y sólo en casos menos frecuentes, la dirección paralela provocará cargas mayores, cuando se trate de una línea de origen de mayor entidad; por ejemplo, una línea de doble circuito, cable LA 110 con vano de viento de 180 m que daría una resultante Rgp = 297 + 241 = 538 daN.
En resumen, que en el estudio de un apoyo de derivación en zona A, si se quiere hacer meticulosamente, hay que tener en cuenta las características de las dos líneas, además de la dirección más desfavorable del viento, su disposición geométrica de las trazas y la componente prevista por el desequilibrio de la tercera hipótesis.
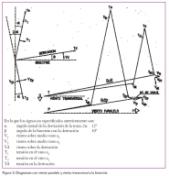
La figura 2 presenta el diagrama de fuerzas de un apoyo de derivación en el que las dos líneas tienen las características del supuesto anterior, matizadas aquí con la inclusión de un ángulo a = 24º que forma la línea de origen con la transversal a la derivación.
Viento transversal a la derivación
También se han señalado en la línea de origen, en la dirección que forma ángulo agudo con la línea derivada, dos vectores que corresponden a los desequilibrios considerados en la tercera hipótesis: Ta = 8 % de Tm, si el apoyo es de alineación o Tj = 50 % de Tm, si el apoyo es de anclaje.
La presión de viento en el vano de viento av vale: Va = pv × av × sen a y es perpendicular a la línea. La presión de viento transmitida al apoyo por medio vano de la derivación vale: Vd = 0,5 ad × pv y es perpendicular a la derivación.
Teniendo en cuenta lo anterior, y a la vista del diagrama, podemos establecer la fórmula para obtener analíticamente el valor de la resultante: Ra para alineación y Rj para anclaje.

Rj para apoyo de anclaje: similar a la anterior, sustituyendo Ta por Tj.
Aplicando a la fórmula (7) los valores de vanos y tensiones que venimos dando como ejemplo, resulta:
Apoyo de alineación:
Ra = v {5682 + (-18)2} = 569 daN
Apoyo suficiente: C-2000
Apoyo de anclaje:
Rj = v (6562 + 1772) = 679 daN
Apoyo necesario: C-3000
Siempre que señalemos apoyos de un esfuerzo determinado, nos estamos refiriendo a apoyos armados con crucetas situadas en el punto teórico de aplicación del esfuerzo útil del apoyo; por ejemplo: un C-2000 armado con cruceta recta en cogolla para el cual la relación carga solicitante/esfuerzo útil es la unidad: La situación de la cruceta por encima de este punto (bóveda), o por debajo (triángulo), con factores de carga mayores o menores que la unidad exigirá introducir correcciones al determinar el esfuerzo necesario.
Viento transversal a la línea de origen
La derivación recibe el viento con un ángulo de 24º y la presión por m será: 0,556 × sen 24 = 0,226 daN/m. Como la presión de viento es proporcional al cuadrado de su velocidad en km/h; podemos deducir una velocidad reducida de viento Vr que actuando sobre el vano de 145 produjera una presión de 0,226 daN/m:
Vr = v[(0,226/0,556) 1202] = 76,5 km/h.
Introducido este valor en un pro-grama que admita velocidades de viento a voluntad, a -5º de temperatura; viento 76,5 km/h; vano 145 m, EDS = 12,18 % (que es el que resulta al aplicar a un vano de 145 m, viento de 120 km/h y Tm = 520 daN), obtenemos una tensión Td = 332 daN.
En el diagrama anterior las presiones de viento serán ahora: Va = 150 × 0,556 = 83,4 daN; y Vd = 40,3 sen 24 = 16,4 daN. Aplicando estos valores a la ecuación anterior resulta.
Ra = v(4262 + (-12)2) = 427 daN
Rj = v(5132 + 1882) = 546 daN
Resulta pues, que con líneas iguales, la dirección más desfavorable del viento es la transversal a la derivación.
Zonas de hielo, B o C (viento en calma)
Si mantenemos la tensión máxima de 520 daN, los dos casos darán los mismos resultados porque sus diferencias están en las cargas verticales y en las flechas que no afectan aquí. Esta tensión máxima con hielo reduce la tensión con viento a 423 daN en zona B y a 249 daN en zona C, que darían valores inferiores a los que obtuvimos en zona A. La fórmula para el hielo será:

Para Rj: sustituir Ta por Tj. Y operando con los mismos valores del ejemplo:
En alineación
Ra = v(5372 + 382) = 539 daN
En anclaje
Rj = v(6262 + 2382) = 670 daN
Este apoyo de derivación está sometido a mayores cargas horizontales en zona A que en zonas B o C. Esto es debido a que para las dos hipótesis, hielo y viento, hemos elegido la misma tensión máxima: 520 daN. Si para viento hubiéramos reducido la tensión a unos 480 ÷500 daN, los esfuerzos no serían mayores que con hielo. Reducción que puede considerarse razonable, ya que las flechas obtenidas son menores que las producidas en zona B con tensión máxima de 520 daN.
Aunque los desequilibrios Ta y Tj, son de 3ª hipótesis anormal, sí se pueden sumar a las tensiones Td de 2ª hipótesis normal siempre que se quieran cumplir las condiciones necesarias para omitir la 4ª hipótesis (en cuyo caso la 3ª hipótesis pasa a ser normal), que es lo corriente en proyectos de líneas de 3ª y 2ª categoría.
Derivación en apoyos de ángulo
Cuando un proyectista tiene que estudiar una línea en derivación y encuentra que, en las proximidades del punto de arranque, la línea de origen tiene un apoyo de ángulo, sucederá que: si la derivación queda del lado convexo del ángulo, el proyectista tenderá a utilizar ese apoyo porque tiene la ventaja de que la resultante de las cargas solicitantes no aumentará sino que disminuirá; por el contrario, si la derivación queda del lado cóncavo tenderá a rehuirlo, lo que significa que, en la práctica se dará con mucha más frecuencia el primer caso que el segundo. Por otra parte, las empresas distribuidoras suelen preferir que las derivaciones se hagan destensadas instalando en la derivación, a pocos metros de la de origen, un apoyo fin de línea que libere a ésta de cargas que no le corresponde soportar. Estos argumentos harían casi impensable que hubiera que estudiar una derivación tensada por el lado cóncavo de un apoyo de ángulo. Sin embargo, como actualmente la elección del trazado viene impuesta generalmente por otras causas que las puramente técnicas como son: edificaciones, exigencias de la propiedad, razones de ecología o de impacto ambiental, apoyos ocupados por otras derivaciones, etc., pueden convertir en necesidad lo que hace un tiempo habría parecido un desatino: enganchar en un apoyo de ángulo en dirección de su bisectriz, y eso es lo que vamos a estudiar a continuación.
Derivación en un apoyo de ángulo cóncavo
Estudiemos los dos casos: que el viento sea paralelo a la bisectriz o que sea transversal a ésta.
La derivación puede NO coincidir con la bisectriz del ángulo, formando con ella un ángulo ß. El efecto del desequilibrio es como en alineación, Ta = 8 % de Tm.
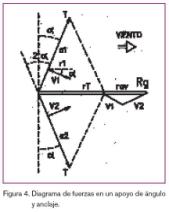
En la figura 3 representamos el diagrama de fuerzas compuesto por las tensiones en las dos líneas, la presión del viento sobre ellas y el desequilibrio del 8 %.
Los vanos y tensiones son los mismos que los del ejemplo que venimos analizando, situamos la bisectriz para obtener: a = 2a/2.
Consideramos dos direcciones de viento:
Dirección P, paralela a la bisectriz. Los signos anteriores llevan el subíndice p.
Dirección T, transversal a la bisectriz. Los signos anteriores llevan el subíndice t.
En los dos supuestos, el sentido de las fuerzas es el mismo, excepto V2t que es opuesto a V2p.
En la resultante Rdp no incluimos el vector Vdp que es absolutamente despreciable y nos complicaría innecesariamente la fórmula que desarrollamos después para obtener analíticamente esa resultante. Lo mismo hacemos con la resultante Rdt del diagrama T en el que despreciamos los vectores V1p y V1t que se contrarrestan y el Vdt cuyo sentido vertical descendente apenas influye sobre la resultante.
Si en los dos diagramas proyectamos sus vectores sobre los ejes de coordenadas (x, y) obtenemos las componentes Rx y Ry de las que podemos sacar las resultantes.
Rd = v(Rx2 + Ry (9)
Diagrama P (10)
Rxp = Tdp cos ß + (T1p + Ta +T2p) sen a + pv × av cos a
Ryp = Tdp sen ß + (T1p + Ta – T2p) cos a
Diagrama T (11)
Rxt = Tdt cos ß + (T1t + Ta +T2t) sen a Ryt = Tdt sen ß + (T1t + Ta – T2t) cos a
A los que, aplicando los valores del ejemplo:
Tdp = 262 Tdt = 515
T1p = T2p = 513,2 T1t = T2t = 270
Ta = 41,6 Ta = 41,6
a = 12º ß = 10º
sen a = 0,208 sen ß = 0,174
cos a = 0,978 cos ß = 0,985
Resulta:
Rdp = v(561,6+96,22) = 570 daN
Rdt = v(628,22 + 130,12) = 641 daN
apoyo C: 2000
El mayor esfuerzo se da en el diagrama T con viento transversal a la bisectriz, que será lo que ocurra siempre que la línea de origen y la derivación tengan el mismo conductor.
Con el método de cálculo convencional: T1 = T2 = Td = 520
Rdp = 829 apoyo C: 3000
Rdt = 749
En zonas de hielo B o C
Rd = 749 apoyo C: 3000
Sólo cuando el conductor de la línea de origen sea de mayor sección que el de la derivación, o sea una línea de doble circuito la primera y sencillo la segunda, en cuyo caso habrá que duplicar los vectores T1, T2 y V1, V2 será donde se dé la posibilidad de encontrar que Rdp > Rdt (sí la línea de origen fuese de doble circuito, del mismo conductor, se produciría ese cambio, las resultantes serían:
Rdt ? 950 daN y Rdp ? 1020 daN.
Apoyos de ángulo y anclaje
Para que un apoyo pueda llegar a cumplir las dos funciones a la vez deberá disponer del esfuerzo útil necesario para cubrir la carga solicitada por el ángulo más el 50 % de la tracción total de todos los conductores que le exige la tercera hipótesis (desequilibrio) en la función de anclaje.
Si las tracciones a ambos lados del apoyo son aproximadamente iguales, su resultante Rg coincidirá con la bisectriz. Sobre uno de los vanos señalamos la tracción Tj que requiere como anclaje. La suma geométrica de estas dos fuerzas (ley del coseno) nos dará el esfuerzo útil que debe proporcionar el apoyo; y teniendo en cuenta que cos (90 -a) = sen a, la fórmula a emplear será:

En el ejemplo: para a = 30º
Rg = 540,9 (tabla 1)
Tj = 520/2 = 260
Rgj = 708 daN apoyo C-3000
Conclusiones
Primera: demostrado que en los apoyos de ángulo es correcto introducir una reducción de tracciones porque el viento no puede ser transversal a las dos alineaciones, hay que decir en seguida que dicha reducción es poco significativa para desviaciones de la traza hasta 60º (a=30) y no merecen modificar el cálculo convencional que resultará con esfuerzos ligeramente sobredimensionados. A partir de los 60º ya puede reconsiderarse el cálculo, por si en algún caso fuera suficiente con un apoyo de esfuerzo inmediatamente inferior al calculado según costumbre. En la tabla 1 se puede observar que un apoyo de 90º de desviación (a=45) (a veces impuesto por el propietario) solicita 645,7 × 3 = 1937 daN, o bien 777,1 × 3 = 2331 daN; apoyo C-2000 ó C-3000, según la forma de cálculo.
Segunda: en los apoyos de derivación pueden ser tan diferentes las características de las dos líneas que será conveniente estudiarlas con las dos direcciones de viento, especialmente si el apoyo de la de origen forma ángulo, como hemos visto en 2.2.1.
Bibliografía
Del Manual técnico de Iberduero, S.A. “Instrucción Técnica AR-20” de 2/6/82, hoja 83, he tomado la fórmula (5) de este trabajo, ilustrada con una figura similar a la figura 1, que se analiza aquí.
Reglamento de líneas eléctricas aéreas de alta tensión: su artículo 30.3 me permite, creo yo, combinar en un apoyo especial, las acciones que corresponden a su función de alineación, anclaje o ángulo, con las que aporta una derivación tensada que engancha en ese apoyo.
Del programa Tense7 para calcular la tensión en un conductor sometido a un viento no transversal.