Avances en la simulación de la transferencia de calor mediante mecanismos de impacto de chorro
Advances in the simulation of heat transfer with impinging jet mechanism
Francisco-Javier Granados-Ortiz (1), Joaquín Ortega-Casanova (1)
Resumen
El uso de chorros para transferencia de calor es un mecanismo con multitud de aplicaciones en ámbitos industriales, como templado de cristales, enfriamiento de dispositivos electrónicos y procesos de mecanizado, entre otras muchas. A pesar de la vasta literatura existente y de ser un problema estudiado desde hace décadas, la gran complejidad de este mecanismo de transferencia de calor aún deja incógnitas no resueltas, como el origen de picos secundarios en la distribución de la transferencia de calor a ciertas separaciones entre chorro y placa y las enormes dificultades para modelar la turbulencia de este tipo de chorros en estudios numéricos. Tanto es así que a veces es más exacto el modelado con simulaciones RANS (Reynolds-Averaged Navier-Stokes) que las normalmente más precisas LES (Large Eddy Simulations). En el presente estudio se muestran los últimos avances logrados en este tipo de simulaciones por parte de los autores para diversas aplicaciones, desde el empleo de simulaciones acopladas hasta técnicas de modelado probabilístico de cuantificación de incertidumbre para obtener márgenes de fiabilidad de las simulaciones computacionales.
Palabras clave: Transferencia de calor, mecanismos de impacto de chorro, simulación numérica, CFD, turbulencia.
Abstract
The use of jets for heat transfer is a mechanism with plenty of applications in industrial areas, such as glass tempering, cooling of electronic devices and machining processes, among many others. Despite the vast existing literature and being a problem studied for decades, the great complexity of this heat transfer mechanism still leaves unresolved questions, such as the origin of secondary peaks in the distribution of heat transfer at certain separations between jet and plate, and the enormous difficulties in modeling the turbulence of this type of jets in numerical studies. Therefore, modeling with RANS (Reynolds-Averaged Navier-Stokes) simulations is sometimes more precise than the usually more accurate LES (Large Eddy Simulations). The present study shows the latest advances made in this type of simulation by the authors for various applications, from the use of coupled simulations to probabilistic uncertainty quantification modeling techniques to obtain reliability margins for computational simulations.
Keywords: Heat transfer, impinging jet mechanics, numerical simulation, CFD, turbulence
Recibido / received: 07/06/2021. Aceptado / accepted: 09/10/2021.
1 Departamento de Ingeniería Mecánica, Térmica y de Fluidos, Escuela de Ingenierías Industriales, Universidad de Málaga, e-mail: fjgranados@uma.es, jortega@uma.es
Doi: 10.23800/10.513
Introducción
Hay infinidad de problemas de ámbito industrial en los que la transferencia de calor es de extrema necesidad, como puede ser el templado de cristales, el enfriamiento de dispositivos electrónicos, procesos de mecanizado, turbinas de gas, intercambiadores de calor y sistemas antivaho de vehículos, entre otros muchos. Para todas estas aplicaciones existe la posibilidad de emplear un método muy eficiente de transferencia de calor: el uso de chorros para convección forzada. El análisis numérico de la transferencia de calor desde una superficie hacia un chorro no es algo nuevo. En numerosos artículos, como en Sagot et al [1], se estudia la incidencia de un chorro sin giro sobre una pared con temperatura constante y se obtienen similitudes entre experimento y simulación numérica mediante unos números de Reynolds turbulentos. Sus resultados numéricos corresponden estrechamente con los resultados experimentales obtenidos en Fenot et al [2], Lee D et al [3] y Baughn et al [4], lo cual le da validez a los modelos numéricos que Sagot et al [1] utilizan para su estudio, y que serán similares a los que se mostrarán en este trabajo. En el presente artículo, además, se discutirán ciertas mejoras realizadas en simulaciones de trabajos anteriores, tanto para aumentar la fiabilidad de la simulación como para mejorar el proceso de transferencia de calor mediante elementos mecánicos, eléctricos o usando fluidos con propiedades termofísicas especiales.
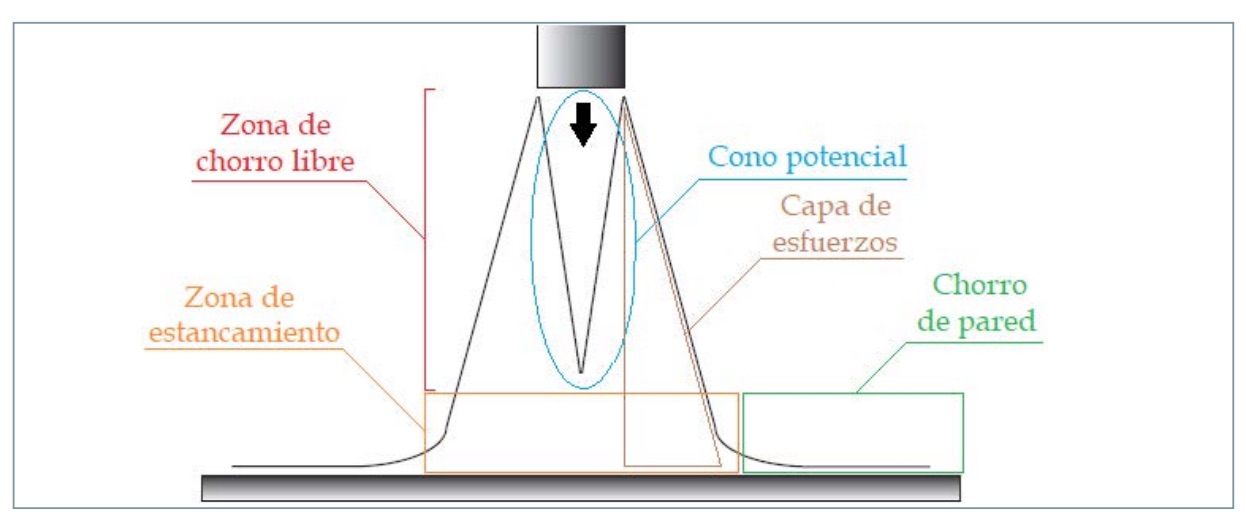
Un ejemplo de chorro de impacto se muestra en la figura 1. La mecánica de este tipo de chorros permite diferenciar varias zonas en su comportamiento. Cuando el chorro sale de la boquilla, se produce en su parte exterior el desarrollo de una capa denominada capa de esfuerzos (shear layer), alrededor de una región de velocidad casi uniforme que se denomina cono o núcleo potencial (potential core), debido a la diferencia entre las velocidades relativas del chorro y el fluido ambiente. La zona inmediatamente debajo de la boquilla y donde incide perpendicularmente el chorro se denomina región de estancamiento. Esta zona se caracteriza por tener el fluido una velocidad nula (realmente ocurre en el punto de estancamiento, que es el punto central de la región), debido al impacto. A partir de ese punto, el flujo cambia su dirección y empieza a moverse perpendicular a la placa. Este flujo es el que se conoce como chorro de pared (wall jet).
Este tipo de mecanismo es óptimo para lograr un enfriado/calentamiento rápido y a un coste relativamente bajo, pues en principio no necesita de mecanismos sofisticados, se pueden utilizar fluidos económicos y no suele necesitar elevadas potencias de trabajo. Dependiendo del problema, nos interesarán unas características concretas. Por ejemplo, si se quiere enfriar un punto muy localizado, nos interesará que se produzca un alto intercambio de calor entre chorro y superficie en el punto o región de estancamiento (punto de impacto). Esta situación puede darse, por ejemplo, en procesos de mecanizado en los que el láser o herramienta de trabajo está aumentando la temperatura en una región muy localizada. Si, además, nos interesa que la transferencia de calor sea global, a lo largo de la superficie sobre la que fluye el fluido, estaríamos buscando un alto valor de la transferencia de calor en valor promedio. Finalmente, hay procesos en los que nuestro interés se halla mucho más enfocado a que la transferencia de calor sea uniforme a lo largo de toda la superficie. Esto es de vital importancia en procesos como el templado de cristales para evitar imperfecciones en su proceso de fabricación.
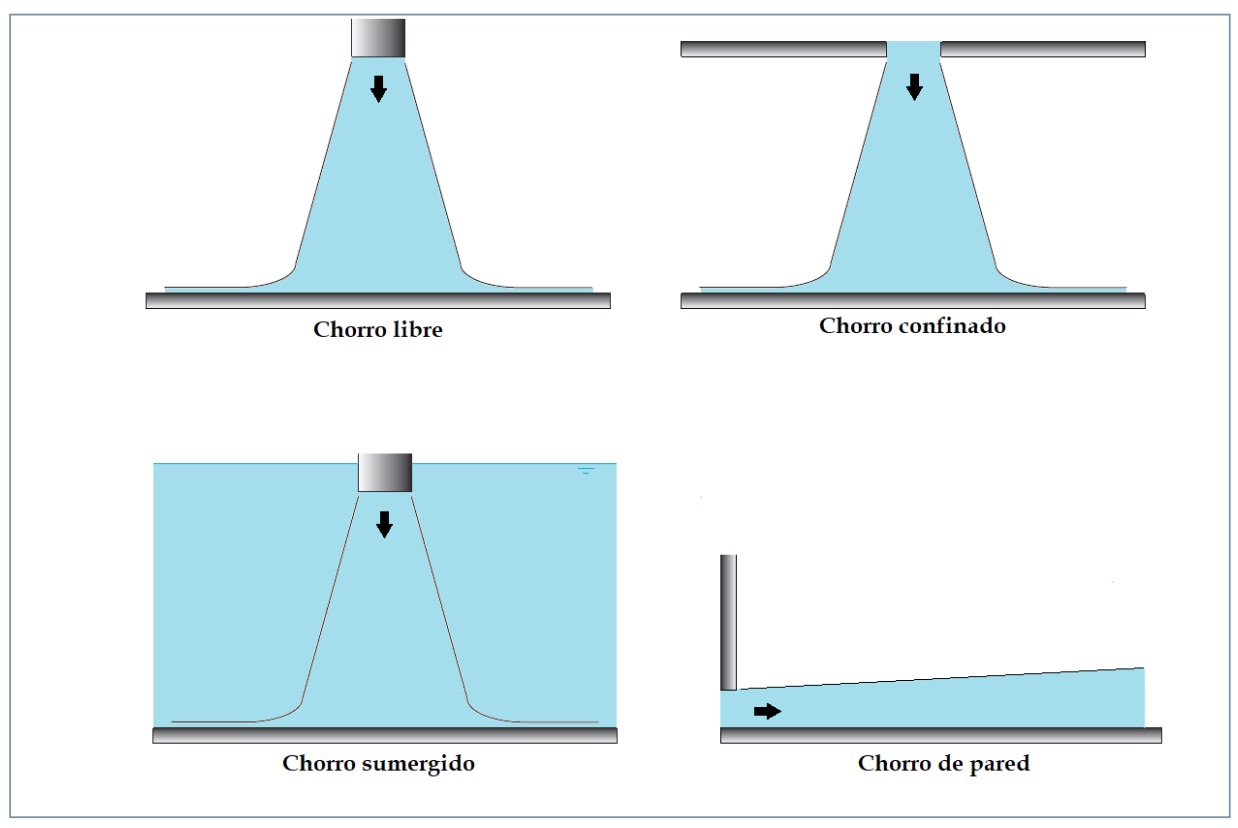
La geometría del problema varía en función de cada aplicación. En la figura 2 se muestran los tipos de chorro que pueden encontrarse en aplicaciones industriales. Cuando no hay ningún tipo de restricción en el dominio más que la superficie de impacto, se denomina chorro de impacto libre. En esta situación, el fluido ambiente, diferente del del chorro, interactúa con total libertad y a presión atmosférica en la mayoría de los casos. Por el contrario, cuando el chorro es de tipo confinado, hay una pared sólida en la parte superior que delimita el dominio (aunque los laterales pueden seguir libres de restricción). Esta situación cambia en cierta medida la distribución de la presión en el dominio. A estos dos tipos de chorro se les puede añadir otro matiz interesante, que es rellenar el dominio a través del que se desarrolla el chorro con el mismo fluido empleado como fluido de trabajo. Un ejemplo sencillo de esta situación sería utilizar un chorro de agua a presión incidiendo sobre una superficie sumergida en un estanque de agua. También existe la opción de utilizar el denominado chorro de pared (wall jet), que consiste en un flujo paralelo a la superficie. Este tipo de chorro se desarrolla también en la lejanía de la zona de impacto para el chorro perpendicular. Aunque no son motivo del presente estudio, el cual se va a centrar en chorros a una velocidad relativamente alta, está la posibilidad de experimentar fenómenos de compresibilidad como ondas de choque, para chorros cuya velocidad sea superior a la del sonido [5]. También es interesante puntualizar que se puede utilizar más de un chorro a la vez, lo que da lugar a los denominados arrays de chorros.
El modelado numérico de chorros incidiendo sobre superficies es un desafío aún abierto. A todo lo añadido anteriormente a la morfología y tipos de chorro habrá que añadir el efecto de la turbulencia. El flujo de un chorro puede ser laminar o turbulento; dicho estado viene determinado por su número de Reynolds. A partir de un determinado valor, el flujo laminar pasa a ser turbulento y aparecen regiones caóticas con fluctuaciones en la velocidad del fluido, a diferencia del comportamiento laminar, en el que todo el flujo se comporta de la misma forma. El modelado de la turbulencia es, a día de hoy, uno de los grandes retos de la física y de las matemáticas, pues aún no se ha logrado resolver analíticamente las ecuaciones de Navier-Stokes, las cuales rigen el movimiento de los fluidos.
Aunque las ecuaciones de Navier-Stokes se pueden resolver numéricamente (v. epígrafe siguiente) con alta precisión para flujos laminares, la turbulencia sigue siendo un problema difícil de simular. Para ello, se utilizan normalmente modelos turbulentos [6]. A pesar de que las simulaciones LES (Large Eddy Simulations) son, tras las prohibitivas computacionalmente pero muy precisas DNS (Direct Numerical Simulations), el método más empleado en el entorno académico para simular con alta precisión el movimiento de flujos turbulentos, existen varios trabajos en los que su predicción en chorros por impacto no es del todo fiable [7-9]. Por otra parte, las simulaciones RANS (Reynolds-Averaged Navier Stokes) representan una opción normalmente menos precisa para modelar la turbulencia, debido a las grandes asunciones que hacen sobre el movimiento turbulento y el uso de modelos configurados en una fuerte base empírica. A pesar de su supuesta menor precisión a la hora de modelar flujos turbulentos, este tipo de simulación ha demostrado en diversos trabajos una muy buena predicción, y ha llegado a capturar el controvertido pico secundario que aparece en ciertas configuraciones de transferencia de calor mediante chorros [10, 11].
Las simulaciones RANS son las más utilizadas en el mundo académico y, sobre todo, industrial. El motivo es que tienen una relativamente alta precisión a la hora de predecir el comportamiento de un amplio rango de aplicaciones en fluidomecánica, a la vez que sus tiempos de simulación son muchísimo menores que con las técnicas LES y DNS, las cuales son más precisas generalmente. Por tanto, es de una suma importancia lograr proporcionar más información sobre la fiabilidad de las RANS. Esto tiene mucha relevancia en entornos industriales, donde se pretende lograr un prototipo en el menor tiempo posible, pero, a la vez, con una técnica que permita tener fiabilidad o confianza en el comportamiento del diseño final. Por este motivo, las técnicas de cuantificación de incertidumbre (UQ, del inglés Uncertainty Quantification) [12] están tomando un papel relevante en el campo de la fluidomecánica computacional (abreviada habitualmente como CFD, de Computational Fluid Dynamics) desde principios de este siglo XXI, aunque el número de aplicaciones de esta técnica es aún demasiado bajo y no muy desarrollado en CFD.
La UQ hace referencia a una cuantificación de cómo la variabilidad de unos parámetros de entrada afecta a la variabilidad de la salida [13]. Esta variabilidad es inherente, por ejemplo, a situaciones físicas reales en las que vibraciones, perturbaciones o defectos geométricos en un diseño tienden a aparecer. La utilización de unas técnicas concretas nos permite reproducir el comportamiento estocástico de un sistema bajo incertidumbre, y así lograr en una simulación una reproducción más fiable del comportamiento del diseño en el mundo real. Estas técnicas pueden tratarse de métodos no probabilísticos o probabilísticos (estos últimos son más exactos y detallados al contener un análisis estadístico), así como intrusivos (requieren modificar el código CFD) o no intrusivos (utilizan como entrada simulaciones deterministas). La importancia de incluir una cuantificación de incertidumbre en la simulación CFD es importante desde dos puntos de vista: el aleatorio y el epistémico. Por una parte, esta permite incluir los efectos de aleatoriedad inherente al comportamiento físico real del sistema (incertidumbre aleatoria o estadística). Esto sucede, por ejemplo, cuando se pretende simular el viento alrededor de las palas de un aerogenerador, el cual puede tener ciertas variaciones debido a condiciones atmosféricas, las cuales seguirán una función probabilística. Otro tipo de incertidumbre es la epistémica. Este tipo de inexactitud se debe a una falta de conocimiento dentro del modelo en sí. Este tipo de incertidumbre se considera reducible, ya que puede aumentarse el conocimiento o sofisticación dentro de un modelo numérico y disminuir esa incertidumbre. Un ejemplo es el uso de modelos para modelar la turbulencia. Cada modelo posee unas características concretas que hacen que haya una incertidumbre epistémica asociada a dicho modelado.
Ambos tipos de incertidumbre se han estudiado clásicamente por separado. Sin embargo, muy recientemente los autores del presente artículo han llevado a cabo un estudio que permite relacionar el impacto de ambos tipos de incertidumbre en simulaciones CFD con turbulencia [14]. Es importante destacar que la interacción de ambas no tiene por qué ser aditiva o lineal, y las interacciones no lineales pueden determinar una cuantificación mucho más realista. La inclusión de técnicas de UQ en simulaciones numéricas de chorros por impacto ha sido ignorada hasta hace poco. Debido a la gran complejidad de la mecánica detrás de este tipo de aplicación, es importante llegar a cuantificar los márgenes de fiabilidad de dichas simulaciones, para así determinar en qué rangos se puede esperar que varíe el comportamiento final de la aplicación final en ingeniería. Esto se verá en detalle a continuación.
En esta investigación se muestran los últimos avances logrados en la simulación de chorros para diversas aplicaciones. Destaca desde el uso de simulaciones acopladas hasta técnicas de modelado probabilístico de cuantificación de incertidumbre, para obtener márgenes de fiabilidad realistas que permitan aumentar la confianza en estas simulaciones computacionales.
El presente artículo se divide en varias secciones. En primer lugar, en el siguiente epígrafe se dan los detalles teóricos y numéricos de la simulación numérica del chorro por impacto. En dicha sección se discute también la precisión esperada con cada método numérico empleado, así como de qué manera se han obtenido márgenes de fiabilidad con las RANS. En el siguiente epígrafe se comentan los últimos avances llevados a cabo para mejorar la transferencia de calor mediante elementos mecánicos, eléctricos o uso de fluidos con características termofísicas especiales utilizando simulaciones numéricas. Finalmente, el último epígrafe se dedica a las conclusiones de este artículo.
Ecuaciones, geometría y problema numérico
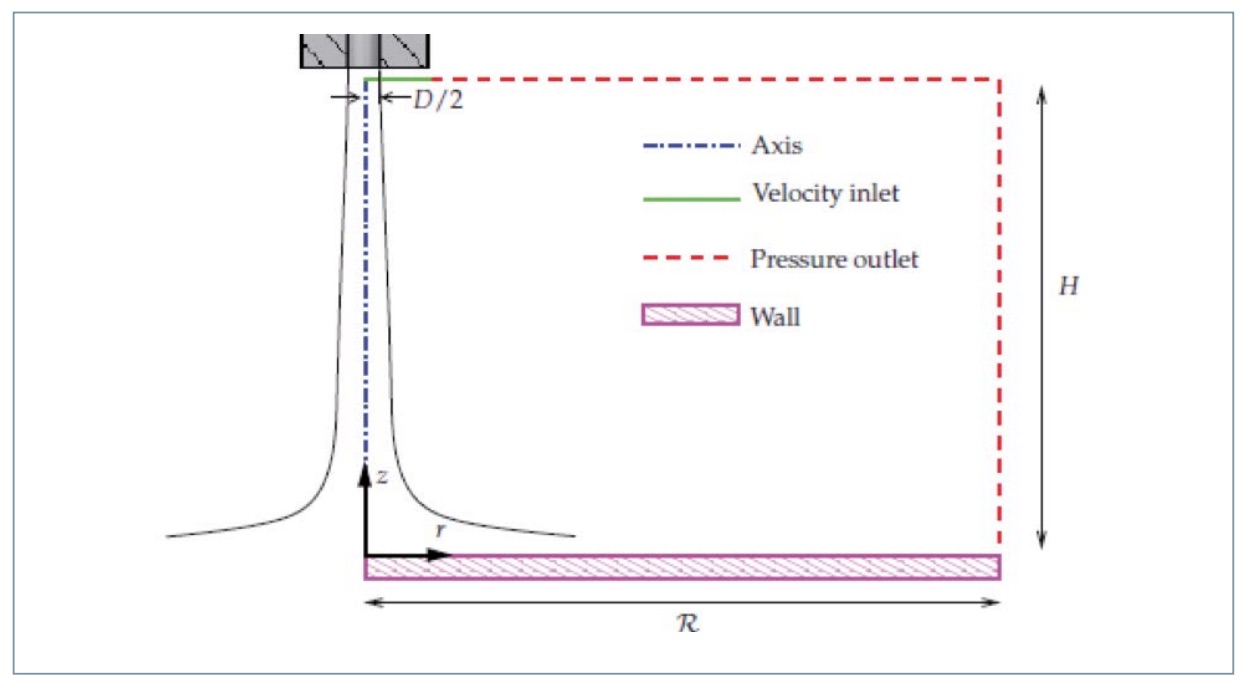
En primer lugar, se va a mostrar la geometría que se empleará en los resultados mostrados en este artículo. El dominio será como se muestra en la figura 3. En dicho dominio se puede encontrar la boquilla del chorro de diámetro , la cual está separada una distancia de la placa. El chorro es libre (no confinado) en esta representación. Así quedaría, por ejemplo, rodeado por el mismo fluido a temperatura y presión atmosféricas si se tratase de aire. Cabe destacar que, bajo los números de Reynolds considerados, el fluido de trabajo se comportará siempre como un flujo incompresible. Siempre que el número de Reynolds y Prandtl sean los mismos (se definen estos números más adelante), dará igual si se considera, por ejemplo, agua o aire. El problema se abarcará bidimensionalmente y, al tratarse de un problema totalmente simétrico, esta gometría bidimensional puede revolucionarse 360 grados alrededor de su eje de simetría y considerarse, por tanto, axilsimétrico. Axis, Velocity inlet, Pressure outlet y Wall son las condiciones de contorno impuestas en FLUENT para resolver el problema numérico, las cuales se explicarán a continuación junto con la descripción teórica del problema.
Para estudiar el régimen del chorro se utilizará el número adimensional de Reynolds, que se define como
donde p es la densidad del fluido, U es la velocidad media del chorro al salir de la boquilla, el diámetro D se ha tomado como longitud característica para este número adimensional por ser lo más común en la literatura y es la viscosidad dinámica.
En primer lugar, se va a describir la transferencia de calor por convección y conducción. Respecto a la convección, esta se rige mediante la ley de enfriamiento de Newton junto con las ecuaciones de Navier-Stokes. La ley de enfriamiento de Newton establece que el flujo de calor entre un fluido y un sólido o entre dos fluidos se puede obtener como
donde
En cambio, la mecánica de fluidos se rige por las ecuaciones de Navier-Stokes, las cuales permiten resolver los campos de velocidad v, temperatura T, presión p y densidad p. Las ecuaciones para el caso de un fluido newtoniano son:
Ecuación de continuidad:
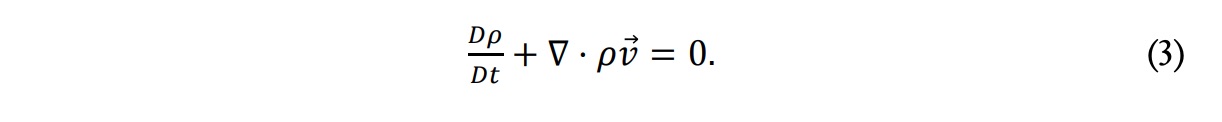Ecuación de cantidad de movimiento:
donde t es el tensor de esfuerzos de Reynolds y pfm son las fuerzas másicas.
Ecuación de energía:
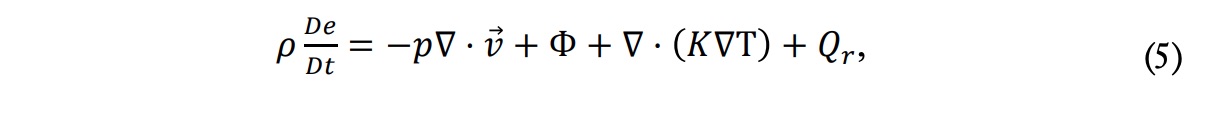donde ? es la función de disipación viscosa de Rayleigh y Qr, es el calor aportado al fluido por unidad de tiempo y volumen. La relevancia de KVT se comenta a continuación. Se han utilizado las derivadas sustanciales D/Dt para considerar que las magnitudes fluidas varían con el tiempo no solo por el movimiento no estacionario, sino porque también cambiará al pasar de un punto espacial a otro.
La transferencia de calor por conducción se rige por la ley de Fourier, la cual indica que existe una relación lineal entre el vector flujo de calor y el gradiente de temperatura tal que:
siendo K la conductividad térmica del fluido. Una vez descrita la transferencia de calor por conducción y convección, se va a proceder a cuantificar la transferencia de calor adimensionalmente. Para ello se va a utilizar el número de Nusselt. Este número cuantifica la transferencia de calor por convección frente la transferencia de calor por conducción. De forma general, el número de Nusselt se define como:
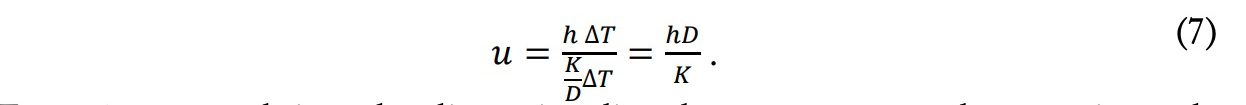Este número se obtiene de adimensionalizar la temperatura en las ecuaciones de Navier-Stokes, y permite cuantificar de manera adimensional la evolución de la transferencia de calor a lo largo de las placas sobre las que incide el chorro mediante el Nusselt local (Nu) y, globalmente, entre todas las placas mediante el , el Nusselt promedio (Nu), siendo ambos Nu = f(r,Re,Pr) y Nu = f(Re,Pr) . Pr es el número de Prandtl, el cual es una propiedad física del fluido (no depende de depende de geome ía ni velocidad) y geometría ni velocidad) y nos sirve para cuantificar la difusión de la cantidad de movimiento frente a la difusión del calor:
donde ? es la difusividad térmica y ? la viscosidad cinemática. Por tanto, hablar del aumento del número de Nusselt, equivaldrá a hablar de aumento de la transferencia de calor. A nivel práctico, el número de Nusselt proporciona una idea de si predomina la transferencia de calor por conducción o por convección; pero como se ha dicho, la conductividad térmica del fluido es una propiedad únicamente de dicho fluido y, por tanto, lo único que variará es el coeficiente de película del numerador del número de Nusselt de la ecuación (7)
Modelado de la turbulencia: El problema del pico secundario en la distribución del Nusselt
Por un lado, como utilizamos un fluido incompresible y Re >> 1, se puede despreciar la variación de la densidad y la disipación viscosa, ya que las fuerzas viscosas son despreciables frente a la convección de la cantidad de movimiento. Por otro lado, en nuestra simulación el régimen del fluido va a ser considerado turbulento y estacionario. Por ello, las ecuaciones RANS de continuidad y cantidad de movimiento escritas en notación tensorial compacta quedarán de la forma:
Ecuación de continuidad:
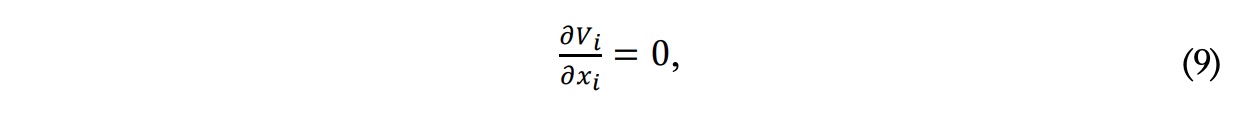Ecuación de cantidad de movimiento:
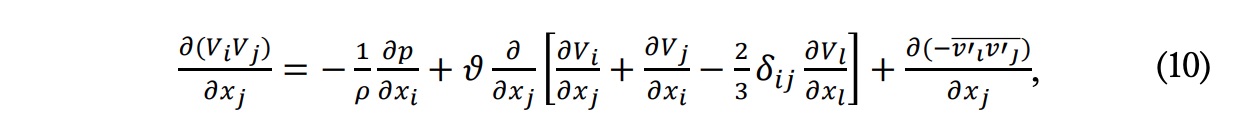Ecuación de la energía:
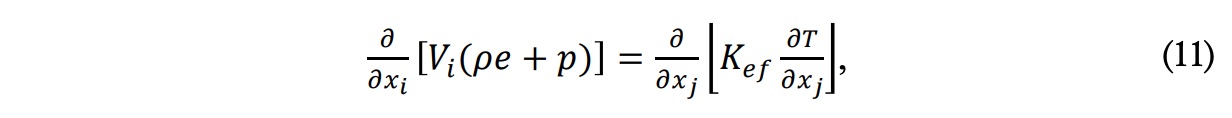donde
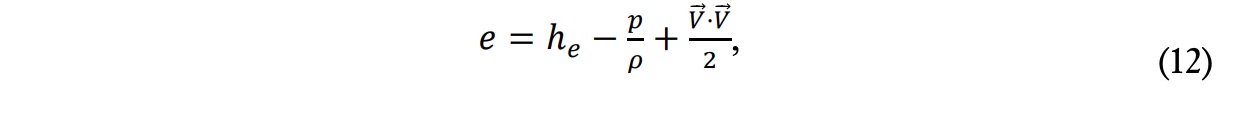donde Vk es la velocidad promedio en la coordenada k (siendo k una notación generalista para cualquiera de las coordenadas en cuestión), V’k las fluctuaciones de la velocidad, e la energía interna, he la entalpía y Kef es la conductividad térmica efectiva, la cual tiene en cuenta la conductividad térmica y la conductividad térmica turbulenta:
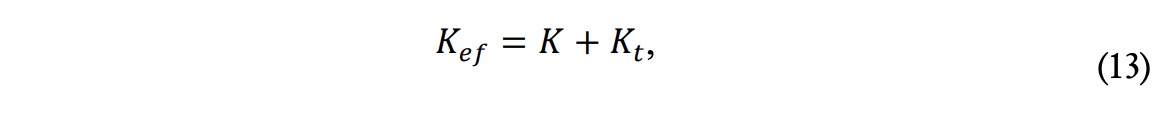siendo
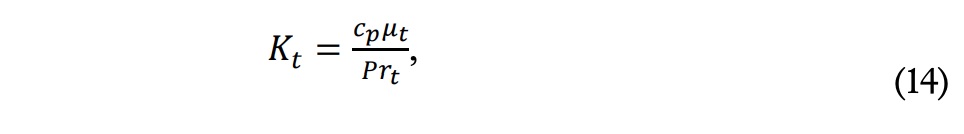y donde cp representa el calor específico, mt, la viscosidad dinámica turbulenta y prt el número de Prandtl turbulento. Para resolver las ecuaciones numéricamente, debemos indicar también las condiciones de contorno del problema. Estas se han mostrado anteriormente en la figura 3, de acuerdo con las opciones que aparecen en FLUENT. Las condiciones son:
- Wall (pared) para la superficie plana de impacto. La placa tiene un flujo constante de calor (de valor arbitrario) y condición de no deslizamiento (no-slip condition).
- Axis (simetría). Como han demostrado varios autores (véase, por ejemplo Petera et al [15], donde simulan el flujo 2D y 3D sin apenas diferencias entre ambos) este tipo de chorro tiene simetría axial. La condición axis impone que los flujos a lo largo del eje sean nulos para todas las variables.
- Inlet para la boquilla eyectora. Esta condición consiste en imponer la velocidad y la turbulencia del flujo que entrará en el dominio y se desarrollará como un chorro.
- Pressure outlet para el dominio libre. Esta condición impone la presión en los límites del dominio y controla la dirección de salida del flujo del dominio.
Para más detalles numéricos sobre estas condiciones, se recomienda ver la documentación de FLUENT [16].
En la ecuación (10), V’k representa, como se ha dicho con anterioridad, las fluctuaciones de la velocidad, las cuales hacen referencia a la turbulencia y son, a priori, desconocidas. Esto hace necesario utilizar modelos turbulentos en las ecuaciones RANS. Respecto al modelo turbulento empleado, se describirá el modelo k-? y en particular, su versión SST (Shear-Stress Transport). Se pondrá mayor énfasis en este modelo turbulento en el presente artículo por ser el utilizado en la mayoría de los trabajos RANS de la literatura y ser, por tanto, el método más recomendado [10, 11, 14]. El modelo SST k-? fue desarrollado aunando de manera efectiva la formulación sólida y precisa del modelo k-? en la región próxima a la pared con la independencia de libre flujo del modelo k-? [16]. Para lograr esto, el modelo k-? se convierte en una formulación del modelo k-?. El modelo SST k-? es similar al modelo k-?, pero incluyendo las ciertas mejoras, como dependencias con el esfuerzo cortante turbulento o términos para la amortiguación de la difusión en la ecuación de ? [16]. Estas características hacen al modelo SST k-? más preciso y fiable para una clase más amplia de flujos (en especial para nuestro caso, el cual posee una zona de estancamiento) que el modelo k-? estándar.
Por tanto, en el estudio de CFD que se aborda aquí se va a tener que resolver, además de las ecuaciones de continuidad, cantidad de movimiento y energía, dos ecuaciones adicionales para modelar la turbulencia con k-?. Las ecuaciones del modelo k-? que gobiernan el modelo son, para estado estacionario y fluido incompresible, las que exponemos a continuación. Para la energía cinética turbulenta (k):
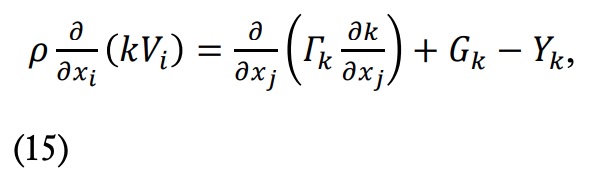y para la disipación específica turbulenta (?):
donde ?_? y ?_k son las difusividades efectivas de k y ?; G_k y G_? son la generación de k y ?, debido a los gradientes de velocidad media, e Y_k y Y_? son la disipación de k y ?. Estos parámetros tienen un tratamiento especial para transformar el modelo k-? en SST k-?, de acuerdo a lo comentado anteriormente. Para no sobrecargar esta sección de fórmulas se recomienda consultar estos detalles en ANSYS [16].
Finalmente, hay que destacar que el impacto de chorros produce un cambio de velocidad brusco en el flujo, el cual conlleva valores altos en la tasa de esfuerzos de cizalladura (shear strain rate, S_ij), y que deriva en una sobreproducción de energía cinética turbulenta que aleja los resultados de la realidad. Para solventar esto, se debe controlar la producción de k. Kato [17] sugiere recurrir a la vorticidad ?_ij en el término de producción de la energía cinética turbulenta, pasando de modelarlo como P_k=?_t S_ij S_ij a P_k=?_t S_ij ?_ij.
Como el flujo en torno a un punto de estancamiento (zona de impacto) es casi irrotacional (?_ij?0), la producción de energía cinética turbulenta queda muy controlada. La utilización de esta corrección (Kato-Launder option o Kato-Launder modification) ha demostrado en la literatura un aumento considerable en la precisión de las simulaciones RANS [11, 15] (Fig. 4).
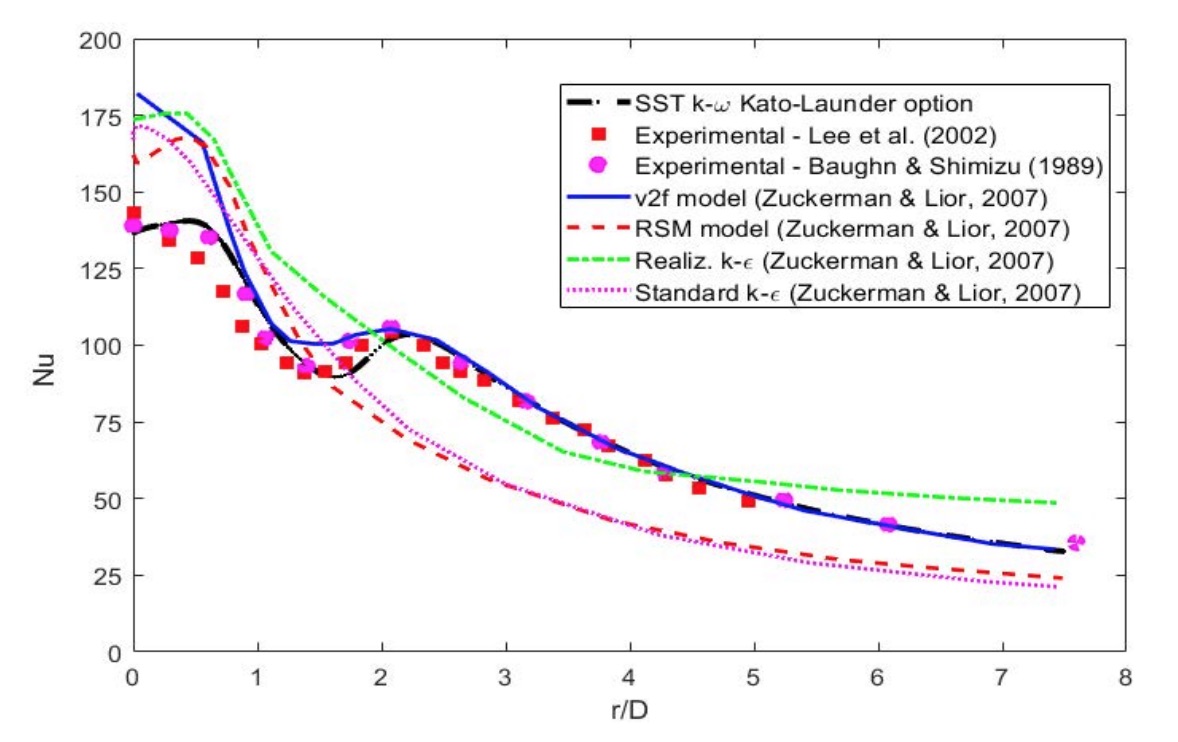
Uno de los hechos más remarcables del uso de un correcto modelo turbulento, como se ha observado con SST k-?, es que se puede lograr reproducir un aspecto importante de la mecánica de la transferencia de calor de este tipo de chorros: el pico secundario de la distribución del número de Nusselt. En la figura 4 se puede observar dicho pico localizado a una distancia de, aproximadamente, 2D del punto de estancamiento, r/D = 0. Este fenómeno no tiene lugar para cualquier configuración geométrica del chorro, sino que aparece cuando la distancia entre boquilla y superficie de impacto es relativamente cercana. Hoogendoorn [19] ratifica esta característica, y se encuentra que no solo es relevante en la aparición del pico secundario, sino que el nivel de turbulencia que presenta el chorro también. Respecto a esta característica tan peculiar, a pesar de que el enfriamiento mediante chorros en aplicaciones ingenieriles ha sido estudiado desde hace varias décadas, tanto experimental como numéricamente, no existe aún un consenso científico común sobre el origen físico de este pico. A pesar de esto, un gran número de autores lo achacan a una transición de laminar a turbulenta de la placa límite [20, 21] o a un aumento repentino de la intensidad turbulenta [22, 23]. Hay también ciertos autores [24] que relacionan que el nucleo o cono potencial (potential core) interactúa con la superficie de impacto y genera esa forma del Nusselt si la distancia es lo suficientemente cercana como para que la placa llegue a modificar el libre desarrollo del cono potencial. Kataoka et al. [25] sugieren que el impacto de los vórtices de mayor tamaño contra la placa produce una variación en las capas adyacentes a la superficie debido al efecto de “renovación” por ese continuo impacto. Finalmente, otros autores atribuyen este fenómeno a la desaparición del gradiente de presión producido en la región de impacto y que afecta a la estabilidad del flujo del chorro, así como a un aumento repentino de la intensidad turbulenta [26].
Si la naturaleza física del pico secundario no está aún clara, conseguir capturarlo numéricamente entraña aún más incógnitas. Una serie de trabajos utilizan simulaciones LES para modelar computacionalmente el comportamiento de la transferencia de calor por impacto de chorro. Sin embargo, a pesar de la amplia literatura científica que respalda la mayor precisión de las simulaciones LES en comparación con las RANS, en la gran mayoría de estos trabajos el pico secundario del Nusselt no ha sido capturado correctamente en estas simulaciones, bien por reproducirlo pero no reproducir fielmente la distribución global del Nusselt [8], bien por simularlo a una localización alejada de la real [7] o bien directamente por no ser reproducido en absoluto [9]. Recientemente, algunos autores han logrado reproducir la distribución del Nusselt y su pico secundario mediante simulaciones LES con cierta precisión [27], aunque con mucha menor semejanza que las RANS mostradas en el presente artículo (v. Fig. 4). Uno de los motivos que se dan en el trabajo numérico en [27] acerca de la presencia del pico secundario es que la aceleración del flujo en la zona de desarrollo de la capa límite está íntimamente ligada al pico secundario, así como una extraordinaria sensibilidad de la simulación respecto al refinamiento del mallado. Esto podría indicar que, al existir una menor sensibilidad de las simulaciones RANS al mallado, al no llegar a simular vórtices a tan pequeña escala, podría contener menor “ruido” numérico (turbulencia de pequeña escala) y permitir capturar mejor el impacto de los vórtices de mayor escala en la transferencia de calor.
Esta enorme sensibilidad de la evolución del Nusselt respecto a la geometría y régimen del chorro refleja una incertidumbre considerable respecto a la fiabilidad de las simulaciones de este tipo. Hay que recordar que si la simulación no nos parece fiable, no tiene mucho sentido su utilización para diseño de mecanismos eficientes de transferencia de calor en aplicaciones reales en ingeniería mecánica. Esto nos lleva a intentar dotar a estas simulaciones de ciertos márgenes de confianza que nos garanticen, al menos, una franja de actuación realista del prototipo. Aquí entra la cuantificación de incertidumbre, UQ (Uncertatinty Quantification).
Inclusión de márgenes de fiabilidad para simulaciones de alta complejidad: cuantificación de incertidumbre (UQ)
Como se ha comentado en el epígrafe anterior, la simulación numérica de este tipo de problemas que presentan pico secundario da lugar a resultados cuya fiabilidad puede ser reducida. En términos generales, la fiabilidad en una simulación tiene un gran impacto en las decisiones en ingeniería, pues la imprecisión de un resultado numérico puede traducirse en encontrar un diseño óptimo computacionalmente que no corresponda con el diseño óptimo real, así como el no detectar situaciones de riesgo para un prototipo (por ejemplo, generación de vibraciones que limiten la vida útil del elemento). Por este motivo, proporcionar márgenes de fiabilidad es de gran importancia.
Para el caso de la simulación de transferencia de calor mediante un chorro, el aspecto que genera más incertidumbre es la presencia del pico secundario. Como se ha visto, no hay aún consenso en la comunidad científica acerca de su origen, pero en lo que sí está de acuerdo la mayoría es en que la turbulencia desempeña un papel importante. Por tanto, el comprobar cómo la incertidumbre en el modelo turbulento afecta al comportamiento de la simulación nos puede dar una referencia acerca de la fiabilidad muy útil. Este tipo de incertidumbre entraría dentro de la de tipo epistémico. Como se ha comentado en el primer epígrafe, la incertidumbre epistémica se asocia a una falta de conocimiento de un modelo, en este caso turbulento, la cual podría eliminarse si se lograra un modelo matemático para la turbulencia más completo, pero que podría suponer recursos computacionales prohibitivos. A pesar de no haber ningún estudio de este tipo de incertidumbre en chorros de impacto, los hay sobre chorros libres que indican la enorme importancia de cuantificar estas imprecisiones [28, 29]. Al dar lugar el impacto a cambios bruscos en velocidad y líneas de corriente, se espera un papel aún más relevante en la presente aplicación.
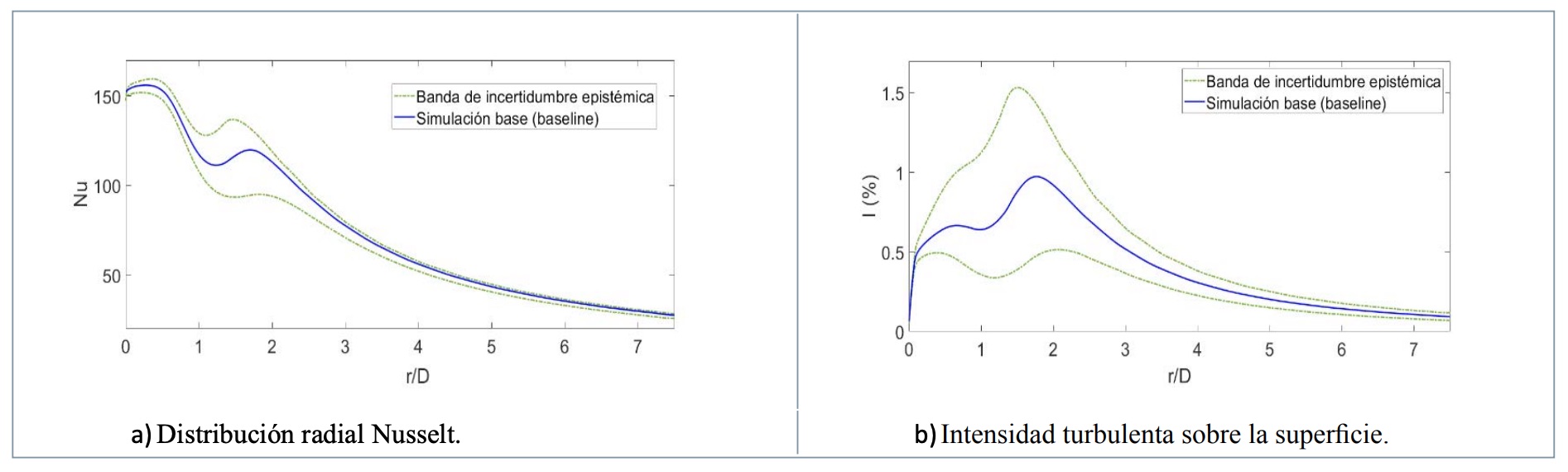
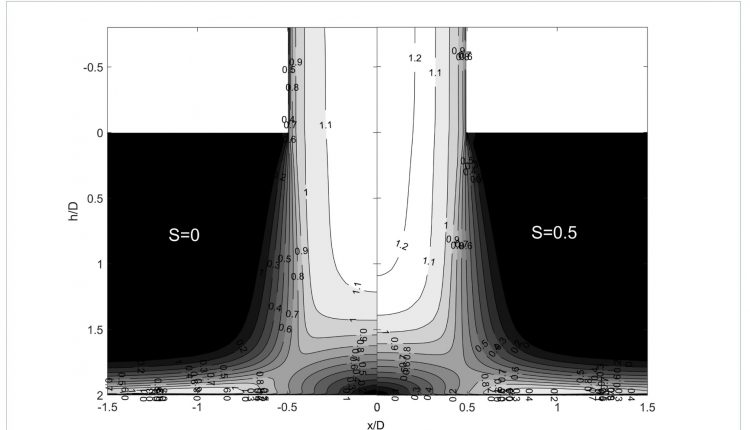
En la figura 5 se muestra un ejemplo de cuantificación de incertidumbre epistémica sobre la simulación de un chorro sumergido a Re=23000, H/ D=2, y con intensidad de giro S=?D/ (2U)=0.5, con la velocidad angular del tubo que genera ese giro en el chorro (estudiado computacionalmente en [11]). El método que se ha empleado para generar las bandas de incertidumbre epistémica es el Eigenspace Perturbation Method [29], método pionero desarrollado por la Universidad de Stanford (EE UU). Este método permite simular los casos más extremos mediante variaciones en el tensor de esfuerzos de Reynolds, el cual contiene las fluctuaciones de velocidad que modelan la turbulencia, por lo que se logra computar una banda con la situaciónes más extremas, pero físicamente realistas. Se puede observar en la figura 5 que, a pesar de que la intensidad turbulenta posee un margen bastante amplio en el pico secundario (una variación, ni más ni menos que del 50%, aproximadamente) y el Nusselt también posee una importante incertidumbre, el modelo turbulento elegido (SST k-?) sería bastante preciso incluso en caso extremo. Como era de esperar, la zona de mayor incertidumbre era el pico secundario, lo cual refleja lo adecuado que resulta simular estas bandas de incertidumbre para conseguir unos márgenes de confianza en la simulación.
Además de la incertidumbre epistémica, de índole principalmente computacional, un mecanismo empleado para una aplicación en ingeniería está sometido a efectos de variabilidad de su entorno. Estos factores pueden ser vibraciones, pequeños errores en la velocidad real de rotación del motor que hace girar al tubo, pérdidas de carga no predichas, deformaciones debidas a montaje-desmontaje de equipos, deterioro en la sensibilidad de las válvulas por su uso continuado, etc. Incluso la tolerancia del aparato con el que se mide está introduciendo incertidumbre a nuestro conocimiento de la situación real. Estos factores normalmente están presentes y se intentan reflejar en los estudios experimentales, por ejemplo, mediante barras de error. Sin embargo, prácticamente nunca se encuentra un estudio de incertidumbre en la simulación computacional en industria. Esto es así porque las técnicas que permiten reconstruir los datos probabilísticos, clásicamente las simulaciones de Monte-Carlo, son extremadamente costosas (puede requerir en torno a miles de simulaciones CFD, lo cual no es permisible en simulaciones de aplicaciones reales). No obstante, la situación ha empezado a cambiar recientemente y técnicas de colocación o de respuesta de superficie [12] han sido utilizadas en algunas simulaciones CFD de chorros libres por los autores con resultados muy precisos y a mucho menor coste. En cuanto a simulaciones de transferencia de calor por impacto de chorros, no hay ningún resultado en la bibliografía, aparte de los realizados por los autores de este artículo [30].
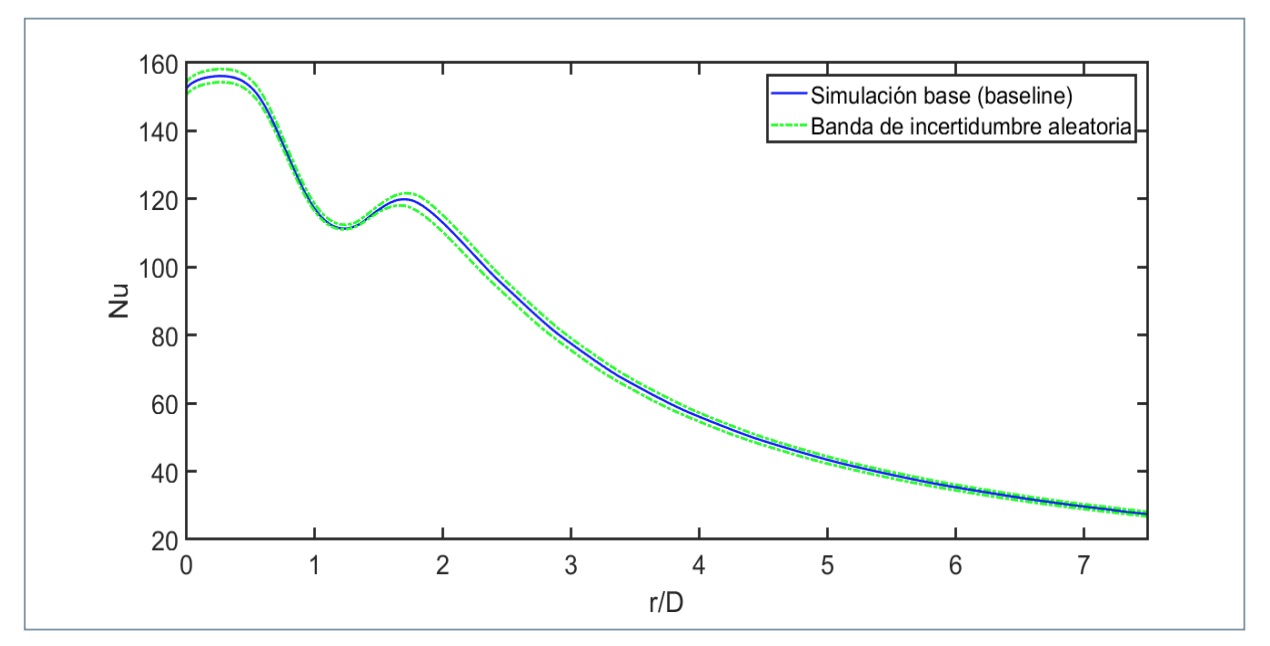
Un hecho, por consiguiente de relevancia, será el tener en consideración también el impacto de la incertidumbre aleatoria. Los autores [30] sugerimos un procedimiento a seguir para poder cuantificar la incertidumbre experimental, que consiste en usar el Método de Colocacion Estocástica. La aplicación del método propuesto en ese trabajo es muy adecuada, pues con muy pocas simulaciones CFD se logran reconstruir los momentos estadísticos de interés. En la figura 6 se muestra cómo quedarían esos resultados aplicados de nuevo en la simulación del chorro a Re=23000, H/D=2 y S=0.5, cuando los parámetros de incertidumbre de entrada son el caudal con un 5% de varianza y la velocidad de giro con un 0,5% de varianza. Estas varianzas se han basado en estudios experimentales del laboratorio de Mecánica de Fluidos de la Universidad de Málaga, una revisión de valores experimentales de la literatura y conversaciones con experimentalistas del Von Kármán Institute for Fluid Dynamics (Bélgica). La gráfica de la distribución del Nusselt muestra que, de nuevo, la parte más sensible a la incertidumbre es el pico secundario. La otra región sensible sería la región de estancamiento, con un impacto muy similar. Esto no ocurría para el caso epistémico. Se concluye, por tanto, que globalmente el pico secundario es la zona más afectada y que incluir márgenes de confianza es necesario para tener una visión más realista sobre el comportamiento del dispositivo en la aplicación en el mundo real.
Estudio de mecanismos de mejora en la transferencia de calor con chorros de impacto mediante simulaciones computacionales
Como se ha comentado a lo largo del presente artículo, el uso de chorros para transferencia de calor por impacto ha sido estudiado durante décadas. No obstante, debido a la alta complejidad en la mecánica de este tipo de chorros, aún hoy se avanza consiguiendo mejorar el proceso en ciertas aplicaciones industriales gracias al uso de CFD. De acuerdo con los resultados que se presentan en este artículo y la revisión bibliográfica que se mostrará en este epígrafe, se podría decir que la inmensa mayoría de estas mejoras se han producido en los últimos 15-20 años, mayormente gracias a los avances en potencia de computación y conocimiento físico del problema. En este apartado se van a clasificar las mejoras en tres partes en función de la naturaleza de los elementos empleados, quedando diferenciadas en mejora mediante i) uso de elementos mecánicos, ii) uso de elementos eléctricos/electrónicos y iii) uso de fluidos con características especiales. Se va a obviar la naturaleza de la clasificación del chorro (libre, confinado, sumergido, en array, etc.) al ser independiente del mecanismo de mejora; y no se van a considerar chorros paralelos a la superficie, pues este tipo de chorro tiene unas características diferentes y está, a su vez, presente en los chorros por impacto una vez que se desarrolla el flujo aguas abajo.
Uso de elementos mecánicos para aumentar la transferencia de calor mediante chorros
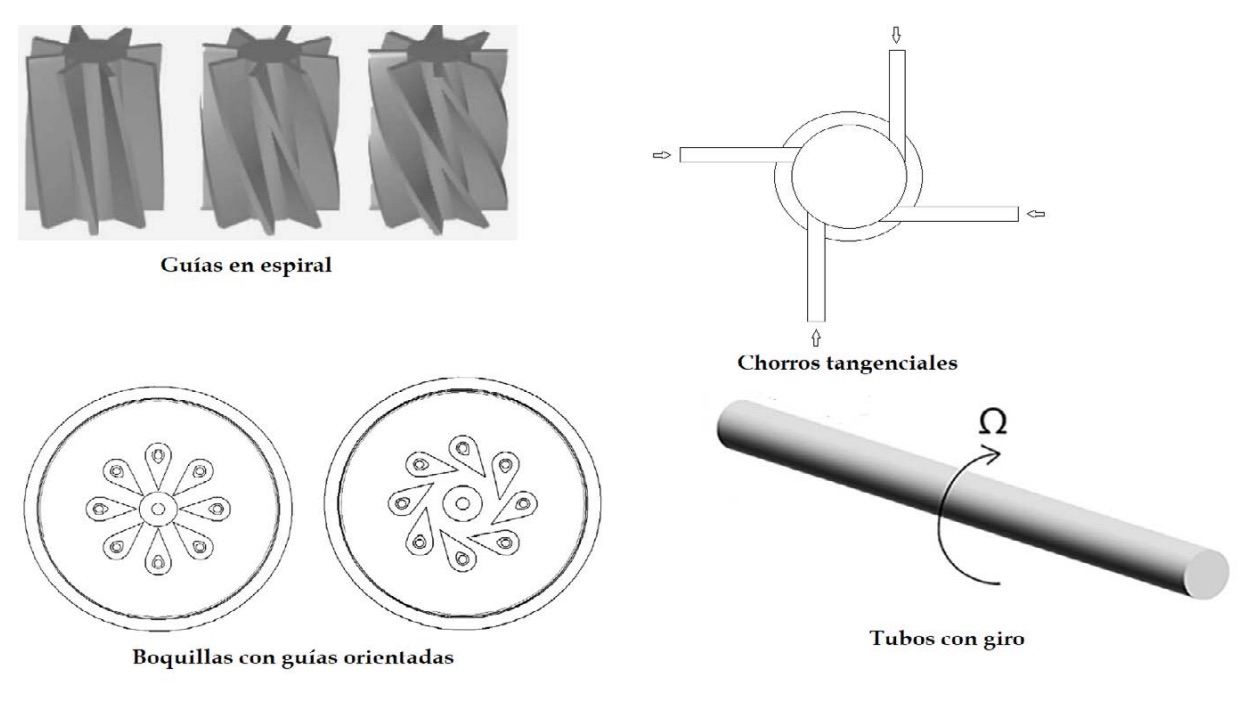
Una de las opciones que existen y que gozan de gran popularidad para aumentar la transferencia de calor mediante impacto de chorros es la generación de giro. Hay numerosos trabajos que demuestran que, para configuraciones concretas (normalmente cuando la boquilla está relativamente cerca de la placa), aumentar el giro aumenta la transferencia de calor [11, 31]. Aunque esto ha sido estudiado desde hace bastante tiempo, la novedad radica en la forma en la que se genera el giro. Dicho giro se puede inducir mediante conductos con guías longitudinales espirales [3], chorros tangenciales [32], boquillas con guías orientadas [10] o tubos sometidos a rotación [11] (Fig. 7), entre otras. Cuando se pretende simular numéricamente uno de estos fluidos, se suele imponer en la condición de contorno de entrada (inlet, en el ejemplo de FLUENT mostrado en la figura 3), el perfil de velocidades. Esto ha permitido a Ortega-Casanova et al [33] el poder simular el comportamiento que tendría un chorro con giro modelado mediante el vórtice de Burger (Burger’s vortex), el cual posee cierta dificultad en el montaje para su generación experimental [34, 35], por lo que la computación numérica es una ventaja en su estudio. En dicho estudio se observó que si el tamaño del núcleo del vórtice (potential core) y la intensidad de giro son pequeñas, se puede lograr una mejora en la transferencia de calor del punto de estancamiento.
Según el mecanismo empleado para proporcionar rotación al chorro, debido a que cada método produce una estructura diferente en él, la distribución del Nusselt a lo largo de la placa es diferente. Se recomienda ver Granados-Ortiz et al. [11], donde se discute esta cuestión y se comparan resultados de diferentes mecanismos de giro. Debido a que en la simulación ha de imponerse un perfil para la velocidad axial, radial y acimutal, una opción sería usar datos experimentales, si existen. Por ejemplo, en Ortega-Casanova et al [10] los autores del presente artículo han caracterizado experimentalmente los perfiles de velocidad a la salida de un chorro con giro inducido mediante guías orientadas y han impuesto esos perfiles en la condición de contorno inlet de la simulación de un chorro sobre diversas superficies. Sin embargo, esto no siempre es posible, pues podría buscarse probar diferentes condiciones (variar el Reynolds o añadir giro si no hubiese, por ejemplo) o fluidos. En esta situación, habría que generar una simulación del flujo que saldría por la boquilla. Por este motivo, en Granados-Ortiz et al. [11] se ha realizado un acoplamiento entre las dos simulaciones (tubo con rotación para generar el flujo con giro y simulación del chorro por impacto). El motivo de acoplar estas dos simulaciones es que: i) para que el flujo esté completamente desarrollado el tubo debe ser muy largo, y ii) los modelos turbulentos óptimos para el tubo y para el chorro impactando no son los mismos. Por tanto, usar simulaciones acopladas dota de enorme flexibilidad: la simulación del tubo con giro se puede reducir a una porción pequeña con condiciones de contorno periódicas y se puede usar un modelo turbulento más preciso, por ser una geometría pequeña y simple.
Respecto al mecanismo de generación de giro, una mención especial merece el hecho de la expansión del chorro a la salida de la boquilla. Para mejorar la transferencia de calor en la zona de estancamiento se prefiere un mecanismo que reduzca la expansión. Por este motivo, Bakirci et al [36] añaden al elemento helicoidal de generación de giro una punta cónica (conical tip), la cual reduce la expansión (probablemente debido al efecto Coanda).
En las simulaciones realizadas por Granados-Ortiz et al. [11] también se observa que usando un tubo con rotación la expansión es mucho menor que cuando se usa otro tipo de generador de giro.
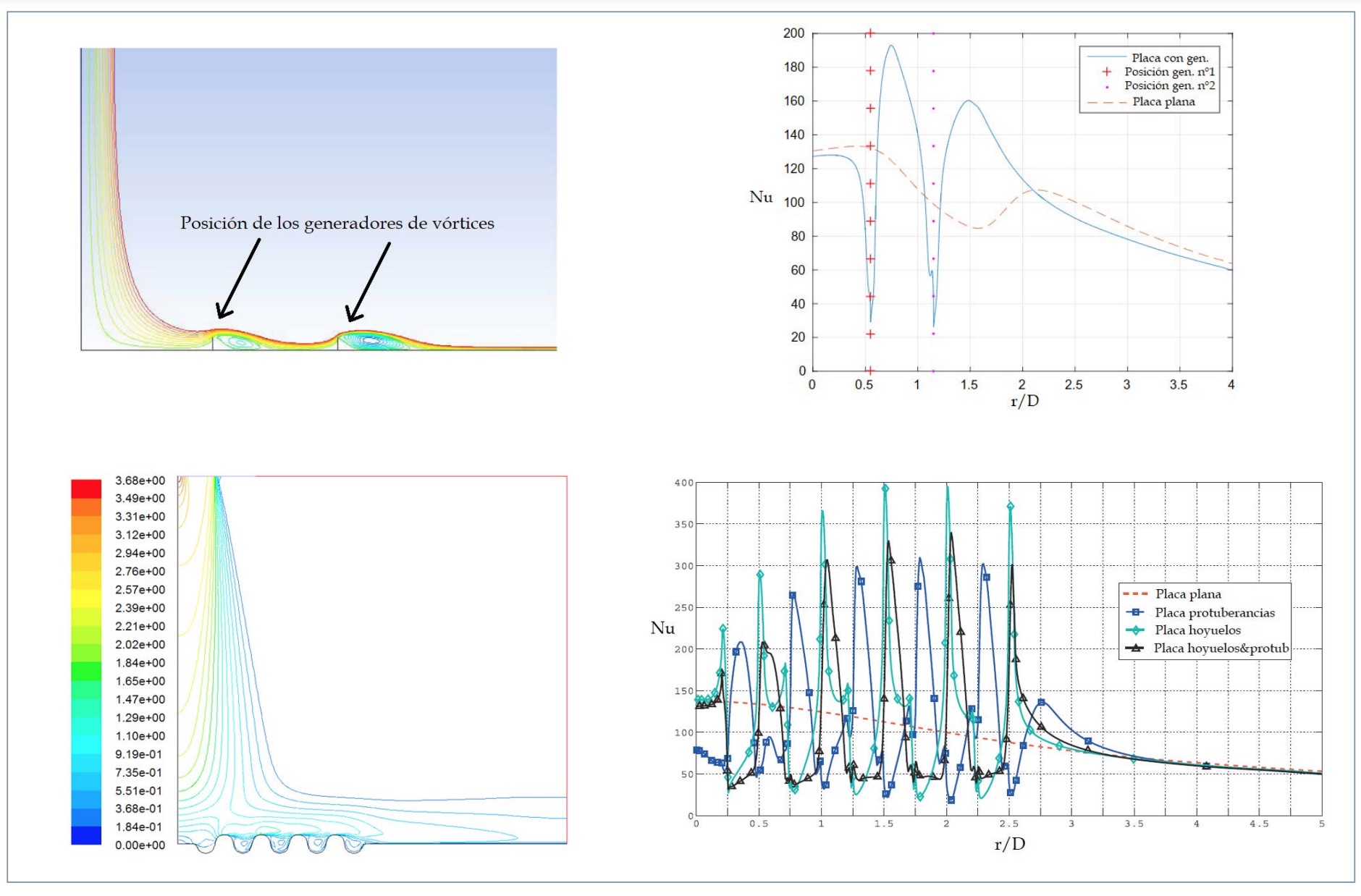
Otra forma de lograr aumentar el intercambio de calor entre placa y flujo sería modificar la geometría de la superficie de impacto. Esto se puede lograr, por ejemplo, pasando de una placa plana a una con hoyuelos, protuberancias o ambas. Estas modificaciones de la geometría tienen dos efectos claramente diferenciados: por un lado, el aumento de la superficie aumenta la transferencia de calor (efecto aleta) y, por otro, el impacto contra los obstáculos de un chorro desarrollado sobre la pared (wall jet) a una velocidad determinada produce un aumento de la vorticidad y creación de recirculaciones que mejoran el fenómeno de intercambio de calor. Por este motivo, en algunos trabajos también se ha optado por simular numéricamente el efecto de la colocación de generadores de vorticidad consistentes en pequeñas aletas verticales [37], cuyo comportamiento se encontró relativamente similar al de las protuberancias, ya que en síntesis ambos son generadores de vorticidad. La ventaja de usar estos elementos es que se producen importantes picos en el Nusselt al pasar estas geometrías, que aumentan así la transferencia de calor localmente, pero también en valor promedio en ciertas configuraciones. En la figura 8 se muestra el comportamiento del chorro para ambas situaciones.
Uso de elementos alimentados por energía eléctrica para aumentar la transferencia de calor mediante chorros
Respecto al uso de elementos eléctricos o electrónicos en el impacto de chorros sobre superficies, en la bibliografía se han encontrado muy pocas novedades al respecto, tanto en resultados experimentales como numéricos. Actualmente no tienen un papel muy relevante en ingeniería térmica ni mecánica. La opción que está tomando más relevancia en la actualidad es el uso de chorros sintéticos o pulsados (synthetic o pulsed jets). Este tipo de chorro se genera de manera discontinua, mediante un pistón o diafragma, que lanza “balas de aire” de mayor proporción que si se usara un ventilador o bomba [38] (Fig. 9). Este tipo de chorros tienen la característica de que conforme se aumenta la separación boquilla-placa pierde compacidad, debido a los vórtices en anillo que se producen por la interacción brusca con el fluido de ambiente y que expanden el flujo [38]. Para más detalles sobre el criterio de formación de este tipo de chorros y su descripción teórica, se recomienda ver Holman et al. [39].
Aunque este tipo de chorros se generan de manera más compleja que los continuos, su modelado computacional es posible, aplicando como condición de contorno una velocidad periódica. Poh et al. [40] simulan en FLUENT un chorro laminar pulsado (Re?1000) para la transferencia de calor. Para las distancias entre boquilla y placa analizadas (H/D=4,5,7,9) para la mayor de ellas se logra, sorprendentemente, un Nusselt local mayor relativamente cerca de la zona de impacto. Sin embargo, se produce una caída muy pronunciada al alejarnos de dicha zona, lo que no pasa con otras distancias. Este estudio, no obstante, carece de comparación con datos experimentales o teóricos para su validación. Alimohammadi et al. [41] demuestran que un diseño con un chorro sintético de impacto pulsado a Re=6000 logra mejorar significativamente la transferencia de calor de un chorro continuo de manera muy significativa si dicho chorro posee una frecuencia elevada y se coloca lejos de la placa. Xu et al. [42] simulan un chorro turbulento confinado cuya generación se produce mediante encendido-apagado intermitente. De nuevo, una elevada frecuencia beneficia y se observa que este pulsado intermitente puede producir un aumento de turbulencia, tamaño de vórtice e inestabilidades en la capa de esfuerzos, así como disminuir la capa límite térmica e hidrodinámica.
Uso de fluidos con características especiales para aumentar la transferencia de calor mediante chorros
Por último, se van a describir aplicaciones de éxito recientes en la simulación de chorros con fluidos de características especiales. Un claro ejemplo de aplicación cada vez más popular en transferencia de calor en termofluidodinámica industrial es el uso de nanofluidos. Como comentan Sheikholeslami et al [43], “los nanofluidos son un nuevo tipo de fluido para transferencia de calor que contiene un número pequeño de partículas de nanotamaño, uniforme y establemente suspendidas en un líquido”. Este tipo de fluidos posee unas características termofísicas muy particulares, ya que el uso de nanopartículas logra aumentar la conductividad térmica de un fluido base y, por consiguiente, mejora la disipación de calor. Sin embargo, el uso de este tipo de fluidos presenta dos problemas: i) a nivel experimental puede no resultar sencillo lograr un nanofluido de trabajo totalmente homogéneo (sin clustering de nanopartículas, propiedades termofísicas constantes, etc.), y ii) a nivel computacional su modelado puede resultar extremadamente complejo. Aún hoy no existe consenso acerca de la mejor manera de simular nanofluidos en CFD. La dificultad en la simulación de nanofluidos radica en que las partículas en el seno del fluido tienen un movimiento complejo, siguiendo un movimiento browniano, cuyo coste de computación es altísimo. A modo de simplificación, muchos investigadores han recurrido a simular el nanofluido como un fluido monofase [44]. Esto permite estimar los valores termofísicos promedio. Sin embargo, varios estudios claman que usar simulaciones multifase es más acertado para ciertas aplicaciones [45]. El problema de las simulaciones multifase es que este tipo de simulación es mucho más costosa computacionalmente hablando. Para lograr reducir los costes, hay una solución intermedia: el modelado mixto (mixture model) [46]. Este tipo de modelado combina las bondades de monofase y del multifase, de manera que se considera que tanto las nanopartículas como el fluido siguen el mismo camino en el flujo. Además, se estima una fracción másica en cada volumen de control asociada a cada fase, y el flujo se resuelve mediante las ecuaciones de continuidad, momento y energía utilizando los valores termofísicos de la mezcla, en lugar de los de cada fase de manera independiente. También hay aplicaciones en las que el nanofluido se ha modelado como fluido no newtoniano, con resultados muy satisfactorios [47].
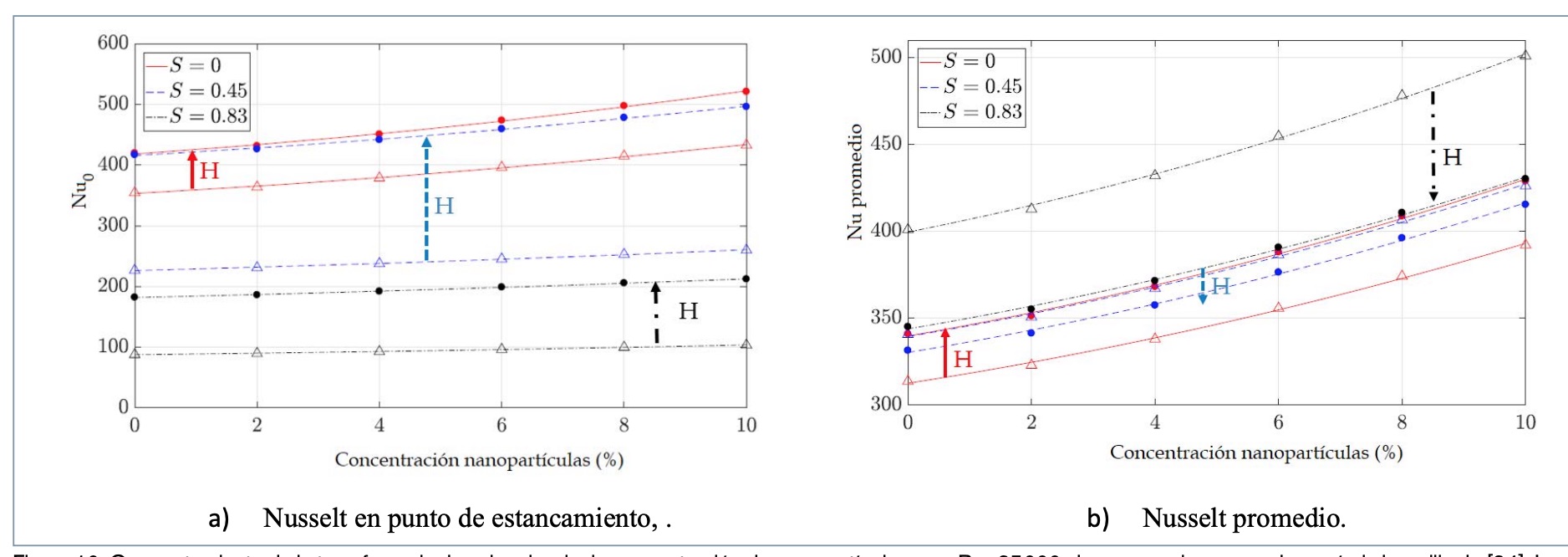
En cuanto a su aplicación en transferencia de calor con chorros, hay bastantes aplicaciones en la literatura, tanto experimentales como numéricas. Sin embargo, la gran mayoría de estos trabajos versan sobre chorros laminares. En la tesis de León-Prieto [48] dirigida por los autores se ha simulado por primera vez en la literatura un chorro turbulento (con y sin giro) para mejorar la transferencia de calor. El modelo utilizado es monofásico, ya que como indican Kilic et al. [49], cuando se trata de un flujo muy turbulento, el movimiento browniano deja de ser significativo, y es más notable en flujos a bajo Reynolds. Los resultados computacionales reflejan que cuantas más partículas de Al2O3 contenga el chorro, mejores resultados de transferencia de calor se logran, como se muestra en la figura 10. Aunque esto parezca una obviedad, en ciertos trabajos se ha detectado que el aumento de la concentración de las nanopartículas a partir de un determinado valor pueden causar un empeoramiento [50].
Un tipo de fluido menos popular en la literatura ingenieril es el no newtoniano. Este fluido posee unas propiedades reológicas muy interesantes, ya que al aumentar los esfuerzos que se le aplican, varía su viscosidad. Esto da lugar a fluidos con un comportamiento shear-thinning (disminuyen su viscosidad) o shear-thickening (aumentan su viscosidad). Ejemplos de este tipo de fluidos son la maicena, el ketchup e incluso la sangre. La ventaja que poseen estos fluidos en su simulación, a diferencia de los nanofluidos, es que esa viscosidad dependiente de los esfuerzos y la temperatura puede modelarse con relativa sencillez, e incluso algunos códigos CFD ya llevan incorporada esa opción. Los modelos más típicos en la literatura son el power-law [48], Carreau [51] y Cross-Power [52], aunque hay más posibilidades [52]. De entre estos, el más común en aplicaciones en ingeniería es posiblemente el power-law, dada su simplicidad y comportamiento preciso para un gran rango de fluidos.
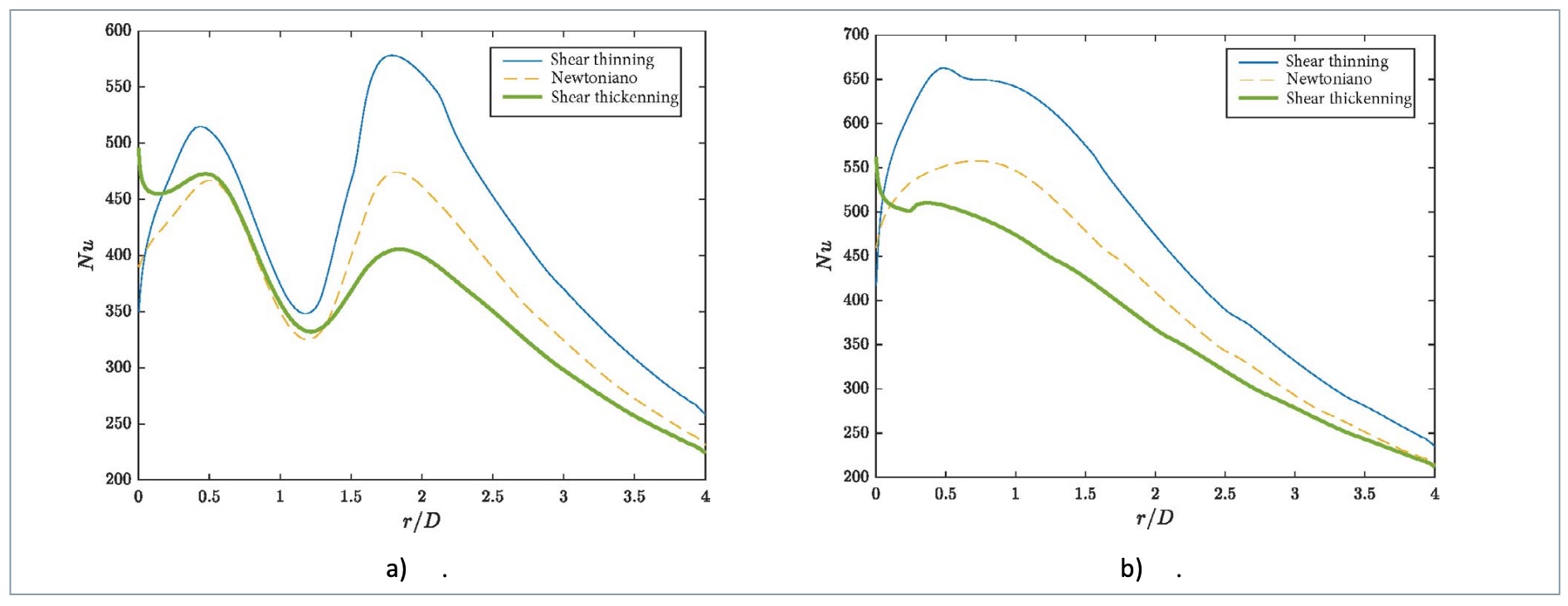
El uso de fluidos no newtonianos para transferencia de calor mediante chorros es un campo no muy investigado en ingeniería mecánica. Todos los artículos en la literatura, tanto en el ámbito experimental como en el computacional, hacen referencia a estudios de chorros laminares (véase, por ejemplo, Chatterjee et al.[51]), a excepción del trabajo [53], que se comentará más adelante. Por tanto, los chorros analizados en la literatura de transferencia de calor están a Reynolds bastante bajos. Ejemplos de aplicaciones de éxito de los modelos de fluido no newtoniano en este tipo de problema a régimen laminar serían Chatterjee et al. [51], que utilizan el modelo de Carreau para chorros confinados cerca de la placa, o Poh et al. [54], que usan la power-law para distancias chorro-placa mayores. Qiang et al. [55] también utilizan el modelo power-law, estudiando un chorro laminar confinado, al cual se le varía el índice de comportamiento del powerlaw y la conductividad térmica del fluido, por lo que se logra una importante mejora en la transferencia de calor entre chorro y placa. Ortega-Casanova et al. [56] simulan un chorro laminar a bajo Reynolds (entre 50 y 200), a diferentes distancias boquilla-superficie e índices del modelo power-law. En este trabajo se observó que el aumento en la distancia boquilla-superficie perjudica a la transferencia de calor y momento, tanto para fluidos shear thickening como shear thinning. Finalmente, en la tesis de Jiménez-Salas [53] dirigida por los autores se ha desarrollado recientemente el primer estudio de chorros turbulentos con fluidos no newtonianos para transferencia de calor, simulando dichos chorros a un Reynolds de 35000 (muy superior a los existentes en la literatura), así como modelarlo también con giro (hasta una intensidad de giro S=0.45). En dicho estudio se observaron varios hechos interesantes. Como se comentó anteriormente, para H/ D=2 los chorros a alto número de Reynolds daban lugar a un pico secundario en la distribución del Nusselt sobre la placa. Al utilizar fluidos no newtonianos en la simulación, cuando los fluidos eran shear thinning, se observó que el pico secundario lograba un valor más alto que la transferencia de calor producida en la zona de impacto (zona de estancamiento). Por otro lado, los fluidos shear thickening presentaban, justo en el punto de estancamiento, un repunte significativo que le daba una estructura inusual a la distribución del Nusselt. En dicho artículo se corroboró que ese repunte se debía a la estrecha relación con la velocidad axial, como ya observaron otros autores en casos de bajo Reynolds [51]. Cuando se le aplica giro al chorro, se observa un cambio radical en la estructura del Nusselt, con la aparición de pequeños picos irrelevantes en los flujos no newtonianos. Se muestra un ejemplo de este comportamiento en la figura 11, para la power-law con índices de comportamiento n=0.8 y n=1.2. Se observa claramente que usar fluidos de tipo shear thinning aumentan significativamente la transferencia de calor global sobre la superficie de impacto.
Conclusiones
La transferencia de calor mediante chorros por impacto es un problema de gran complejidad física que hace que los estudios numéricos sean de gran complejidad. En el presente artículo se han detallado los últimos avances más significativos en la simulación computacional de transferencia de calor mediante este mecanismo, especialmente por parte de los autores del presente artículo, así como algunas discusiones y aplicaciones presentes en la literatura más reciente. Los avances mencionados incluyen un procedimiento a seguir para lograr capturar el pico secundario de la distribución de la transferencia de calor sobre una placa mediante simulaciones RANS, el uso de técnicas de cuantificación de incertidumbre experimental en modelos numéricos, cuantificación de incertidumbre epistémica debido a modelos turbulentos, generación de giro por imposición de velocidad o acoplamiento de simulaciones, aumento de vorticidad, uso de chorros pulsados, nanofluidos y fluidos no newtonianos. Todas estas características se han analizado desde un punto de vista numérico.
Los resultados mostrados permiten lograr un importante aumento en la fiabilidad de estas simulaciones por diversos motivos. Las simulaciones RANS han demostrado ser más precisas que las LES si se utilizan ciertas correcciones, como la modificación de Kato-Launder. Asimismo, se recomienda complementar este tipo de simulación con técnicas de cuantificación de incertidumbre aleatoria, pues se ha logrado replicar el comportamiento probabilístico del sistema en simulaciones CFD gracias a técnicas de colocación estocástica. Por último, se recomienda el complementar el estudio CFD con una cuantificación de la incertidumbre epistémica mediante técnicas como el Eigenspace Perturbation Method. Idealmente, la cuantificación de incertidumbre aleatoria y epistémica debe ser combinada, para lograr simular las interacciones existentes entre ambas, pues se ha demostrado que no son totalmente independientes.
Agradecimientos
Los autores agradecen la financiación recibida a través de los fondos UMA18-FEDERJA-184 y las ayudas para contratación de personal investigador doctor del Plan Andaluz de Investigación, Desarrollo e Innovación de la Junta de Andalucía. Asimismo, agradecen el código UDF para cuantificación de incertidumbre epistémica proporcionado por el Centre of Turbulent Research de la Universidad de Stanford (EE UU).
Los autores también agradecen la supervisión en la consecución de algunos de los resultados por parte del Prof. C. H. Lai de la University of Greenwich (Reino Unido) y al Dr. D. Guariglia & Prof. C. Schram del Von Karman Institute for Fluid Dynamics (Bélgica) por las sugerencias en las incertidumbres experimentales en instalaciones de chorros, así como el trabajo realizado por Manuel Jiménez y Lucía León en sus respectivas tesis de fin de grado.
Referencias
[1] Sagot B., Antonini G., Christgen A., Buron F. “Jet impingement heat transfer on a flat plate at a constant wall temperature”, International Journal of Thermal Sciences 47, 1610-1619 (2008).
[2] Fenot M., Vullierme J. J., Dorignac E. “Local heat transfer due to several configurations of circular air jets impinging on a flat plate with and without semi-confinement”, International Journal of Thermal Sciences 44, 665-675 (2005).
[3] Lee D. H., Won S. Y., Kim Y. T., Chung Y.S. “Turbulent heat transfer from a flat surface to a swirling round impinging jet”, International Journal of Heat and Mass Transfer 45, 223-227 (2002).
[4] Baughn J.W., Hechanova A. E., Yan X. “An experimental study of entrainment effect on the heat transfer from a flat surface to a heated circular impinging jet”, Journal of Heat Transfer 113, 1023-1025 (1991).
[5] Chin C., et al. “Investigation of the flow structures in supersonic free and impinging jet flows”, Journal of Fluids Engineering 135 (3), (2013).
[6] Celik I. “RANS/LES/DES/DNS: The future prospects of turbulence modeling”, Journal of Fluids Engineering 127 (5), 829-830 (2005).
[7] Shum-Kivan F., Duchaine F., Gicquel L. “Largeeddy simulation and conjugate heat transfer in a round impinging jet”, ASME Turbo Expo 2014: Turbine Technical Conference and Exposition (2014).
[8] Uddin, N. “Turbulence modeling of complex flows in CFD”, Tesis Doctoral, University of Stuttgart, Stuttgart (2008).
[9] Hällqvist, T. “Large eddy simulation of impinging jets with heat transfer”, Tesis Doctoral, Royal Institute of Technology, Stockholm (2006).
[10] Ortega-Casanova J., Granados-Ortiz F.-J. “Numerical simulation of the heat transfer from a heated plate with surface variations to an impinging jet”, International Journal of Heat and Mass Transfer 76, 128-143 (2014).
[11] Granados-Ortiz F.-J., Ortega-Casanova J., Lai C.-H. “Two-step numerical simulation of the heat transfer from a flat plate to a swirling jet flow from a rotating pipe”, International Journal of Numerical Methods for Heat & Fluid Flow 30 (1), 143-175 (2019).
[12] Granados-Ortiz F.-J., et al. “On the influence of uncertainty in computational simulations of a high-speed jet flow from an aircraft exhaust”, Computers & Fluids 180, 139-158 (2019).
[13] Saltelli A., Tarantola S., Campolongo F., Ratto M., Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models, John Wiley & Sons Ltd. (2004).
[14] Granados-Ortiz F.-J., Ortega-Casanova J. “Quantifying & Analysing Mixed Aleatoric and Structural Uncertainty in Complex Turbulent Flow Simulations”, International Journal of Mechanical Sciences 188, 105953 (2020).
[15] Petera K., Dostál M. “Heat transfer measurements and CFD simulations of an impinging jet”, EPJ web of conferences 114, 02091 EDP Sciences (2016).
[16] ANSYS. “Fluent 6.3 User’s Guide”, Fluent Incorporated, Lebanon (2005).
[17] Kato, M. “The modelling of turbulent flow around stationary and vibrating square cylinders”, Turbulent Shear Flow 1, 10-4 (1993).
[18] Zuckerman N., Lior N. “Radial slot jet impingement flow and heat transfer on a cylindrical target”, Journal of Thermophysics and Heat Transfer 21 (3), 548-561 (2007).
[19] Hoogendoorn C. J. “The effect of turbulence on heat transfer at a stagnation point”, International Journal of Heat and Mass Transfer 20 (12), 1333- 1338 (1977).
[20] Gardon R., Akfirat J.C. “The role of turbulence in determining the heat-transfer characteristics of impinging jets”, International Journal of Heat and Mass Transfer 8 (10), 1261-1272 (1965).
[21] Lee J. and Lee S.-J. “The effect of nozzle configuration on stagnation region heat transfer enhancement of axisymmetric jet impingement”, International Journal of Heat and Mass Transfer 43 (18), 3497-3509 (2000).
[22] Ahmed Z. U., Al-Abdeli Y. M., Guzzomi F. G. “Flow field and thermal behaviour in swirling and nonswirling turbulent impinging jets”, International Journal of Thermal Sciences 114, 241-256 (2017).
[23] O’Donovan T. S., Murray D. B. “Jet impingement heat transfer. Part II: A temporal investigation of heat transfer and local fluid velocities”, International Journal of Heat and Mass Transfer 50 (17-18), 3302-3314 (2007).
[24] Ashforth-Frost S., Jambunathan K., Whitney C. “Velocity and turbulence characteristics of a semiconfined orthogonally impinging slot jet”, Experimental Thermal and Fluid Science 14 (1), 60-67 (1997).
[25] Kataoka K., Suguro M., Degawa H., Maruo K., Mihata I. “The effect of surface renewal due to large-scale eddies on jet impingement heat transfer”, International Journal of Heat and Mass Transfer 30 (3), 559-567 (1987).
[26] Kestin J., Maeder P. F., Wang H. E. “Influence of turbulence on the transfer of heat from plates with and without a pressure gradient”, International Journal of Heat and Mass Transfer 3 (2), 133-154 (1961).
[27] Uddin N., Neumann S. O., Weigand B. “LES simulations of an impinging jet: On the origin of the second peak in the Nusselt number distribution”, International Journal of Heat and Mass Transfer 57 (1), 356-368 (2013).
[28] Mishra A., Iaccarino G. “Uncertainty estimation for Reynolds-Averaged Navier–Stokes predictions of high-speed aircraft nozzle jets”, AIAA Journal, 3999-4004 (2017).
[29] Mishra A., Mukhopadhaya J., Iaccarino G., Alonso J. “Uncertainty estimation module for turbulence model predictions in SU2”, AIAA Journal 57 (3), 1066-1077 (2019).
[30] Granados-Ortiz F. J., Ortega-Casanova J., Lai, C. H. “Propagation of Uncertainty in a Rotating Pipe Mechanism to Generate an Impinging Swirling Jet Flow for Heat Transfer from a Flat Plate”, Engineering with Computers 1-30 (2020).
[31] Rose W. “A swirling round turbulent jet: Part 1. mean-flow measurements”, Journal of Applied Mechanics 29 (4), 615-625 (1962).
[32] Yan, X., Saniei, N. “Heat transfer measurements from a flat plate to a swirling impinging jet”, International Heat Transfer Conference August 23-28 5, 497-502, Kyongiu (1998).
[33] Ortega-Casanova J., Castillo-Sanchez S. I. “On using axisymmetric turbulent impinging jets swirling as Burger’s vortex for heat transfer applications. Single and multi-objective vortex parameters optimization”, Applied Thermal Engineering 121, 103-114 (2017).
[34] Ahmed Z. U., Al-Abdeli Y. M., Guzzomi F. G. “Impingement pressure characteristics of swirling and non-swirling turbulent jets”, Experimental Thermal and Fluid Science 68, 722-732 (2015).
[35] Ahmed Z. U., Al-Abdeli Y. M., Guzzomi F. G. “Heat transfer characteristics of swirling and nonswirling impinging turbulent jets”, International Journal of Heat and Mass Transfer 102, 991- 1003 (2016).
[36] Bakirci K., Bilen K. “Visualization of heat transfer for impinging swirl flow”, Experimental thermal and fluid science 32 (1), 182-191 (2007).
[37] Ortega-Casanova J., Molina-Gonzalez F. “Axisymmetric numerical investigation of the heat transfer enhancement from a heated plate to an impinging turbulent axial jet via small vortex generators”, International Journal of Heat and Mass Transfer 106, 183-194 (2017).
[38] Remsburg R., Lucas T., Binshtok R. J. “Practical CFD modeling of synthetic air jets for thermal management of electronics”, 26th Annual IEEE Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), February 18-28 (2010).
[39] Holman, R., et al. “Formation criterion for synthetic jets.” AIAA journal 43 (10), 2110-2116 (2005).
[40] Poh, H. J., Kumar, K., Mujumdar, A. S. “Heat transfer from a pulsed laminar impinging jet”, International Communications in Heat and Mass Transfer 32 (10), 1317-1324 (2005).
[41] Alimohammadi, S., Persoons, T., Murray, D. B. “A numerical-experimental study of heat transfer enhancement using unconfined steady and pulsating turbulent air jet impingement”, International Heat Transfer Conference Digital Library, Begel House Inc. (2014).
[42] Xu P., Yu B., Qiu S., Poh H. J., Mujumdar A. S. “Turbulent impinging jet heat transfer enhancement due to intermittent pulsation”, International Journal of Thermal Sciences 49 (7), 1247-1252 (2010).
[43] Sheikholeslami, M., Ganji, D. D. “Chapter 3–Nanofluid Flow and Heat Transfer in an Enclosure”, Hydrotherm. Anal. Eng. Control Volume Finite Elem. Method 1, 31-76 (2015).
[44] Islami S. B., Dastvareh B., Gharraei R. “Numerical study of hydrodynamic and heat transfer of nano
[45] fluid flow in microchannels containing micromixer”, International Communications in Heat and Mass Transfer 43, 146-154 (2013).
[46] Peng W., Jizu L., Minli B., Yuyan W., Chengzhi H. “A numerical investigation of impinging jet cooling with nanoflids”, Nanoscale and Microscale Thermophysical Engineering 18 (4), 329-353 (2014).
[47] Saberi M., Kalbasi M., Alipourzade A. “Numerical study of forced convective heat transfer of nanofluids inside a vertical tube”, International Journal of Thermal Technology 3 (1), 10-15 (2013).
[48] Kamali R., Binesh A. R. “Numerical investigation of heat transfer enhancement using carbon nanotube-based non-Newtonian nanofluids”, International Communications in Heat and Mass Transfer 37 (8), 1153-1157 (2010).
[49] León-Prieto L. “Estudio numérico axilsimétrico a alto número de Reynolds de la transferencia de calor entre una placa plana y un chorro de un nanofluido que impacta sobre ella”, Tesis de Fin de Grado, Universidad de Málaga, Málaga (2019).
[50] Kilic M., Ali H. M. “Numerical investigation of combined effect of nanofluids and multiple impinging jets on heat transfer”, Thermal Science 23 (5 Part B), 3165-3173 (2019).
[51] Nguyen C. T. Galanis N., Polidori G., Fohanno S., Popa C. V., Le Bechec, A., “An experimental study of a confined and submerged impinging jet heat transfer using Al2O3-water nanofluid”, International Journal of Thermal Sciences 48 (2), 401-411 (2009).
[52] Chatterjee A., Dhingra S., Kapur S. S. “Laminar impinging jet heat transfer with a purely viscous inelastic fluid”, Numerical Heat Transfer: Part A: Applications 42 (1-2), 193-213 (2002).
[53] Karimi S., Dabagh M., Vasava P., Dadvar M., Dabir B., Jalali P. “Effect of rheological models on the hemodynamics within human aorta: CFD study on CT image-based geometry”, Journal of NonNewtonian Fluid Mechanics 207, 42-52 (2014).
[54] Jiménez-Salas M. “Estudio CFD axilsimétrico a alto número de Reynolds de la transferencia de calor entre una placa plana y un chorro de fluido newtoniano y no-newtoniano que impacta sobre ella”, Tesis de Fin de Grado, Universidad de Málaga, Málaga (2019).
[55] Poh H. J., Kumar K., Chiang H. S., Mujumdar A. S. “Heat transfer from a laminar impinging jet of a power law fluid”, International Communications in Heat and Mass Transfer 31 (2), 241-249 (2004).
[56] Qiang Y., Wei L., Luo X., Jian H., Wang W., Li F. “Heat Transfer and Flow Structures of Laminar Confined Slot Impingement Jet with Power-Law Non-Newtonian Fluid”, Entropy 20 (10), 800 (2018).
[57] Ortega-Casanova J., Jimenez-Canet M., GalindoRosales F. J. “Numerical study of the heat and momentum transfer between a flat plate and an impinging jet of power law fluids”, International Journal of Heat and Mass Transfer 141, 102-111 (2019).
