Ajuste empírico de reguladores PID en cadena cerrada con Matlab

La obtención de los parámetros de un regulador PID se puede conseguir eficazmente con el método de Ziegler-Nichols.
Introducción
Son múltiples las técnicas de control existentes para los procesos en el ámbito de la industria. Pero, a pesar de ello, la inmensa mayoría en su implementación emplea controladores PID (Proporcional, Integral y Derivativo); algunos autores elevan el porcentaje de utilización a un 90%. Por tanto, pese a los numerosos estudios llevados a cabo en el ámbito de la regulación, incluso introduciendo la utilización de la inteligencia artificial en este terreno, se denota que el empleo de este controlador sigue siendo masivo por diversas razones, como: robustez, fiabilidad, relativa simplicidad, tolerancia a fallos, etc.
Desde su descubrimiento por parte de Nicholas Minorsky en el 1922 que formula la ley de control de los reguladores PID hasta la actualidad, son muchos los estudios llevados a cabo sobre este regulador. En el presente texto se aborda el método de ajuste empírico para cadena cerrada conocido como el método de Ziegler-Nichols. Se emplearán diferentes funciones de transferencia para observar sus resultados en cada caso.
Para el estudio, en este documento se utiliza Matlab, pero su implementación podría ser llevada a cabo en cualquier lenguaje de programación. Se emplea Matlab, sobretodo, por la facilidad de implementación de los sistemas de control en este entorno, así como de mostrar los resultados obtenidos, y, por último, también porque es el más empleado en el estudio de estos sistemas.
El regulador PID
La denominada versión de “libro de texto” para la definición del controlador PID viene dada por la ecuación:
u(t) = K [e(t) +1 te(t)dt + Tdde(t) ] (1)
Ti o dt
donde u es la variable de control y e es el error de control dado por e = ySP – y (diferencia entre la referencia especificada por la entrada y la salida medida del proceso). De este modo, la variable de control es una suma de tres términos: el término P, que es proporcional al error; el término I, que es proporcional a la integral del error; y el término D, que es proporcional a la derivada del error. Los parámetros del controlador son: la ganancia proporcional K, el tiempo integral Ti y el tiempo derivativo Td.
Existen múltiples formas para la representación de un regulador PID, pero para la implementación del regulador PID utilizada definida en la fórmula anterior y más comúnmente conocida como forma paralela, mostrada en representación de bloques se expone a continuación (figura 1).
La fórmula del controlador para este gráfico viene dada por la siguiente expresión:
GC(S) = k +Ki / S+ S · kd (2)
Los términos de esta expresión se corresponden de la siguiente manera con los de la ecuación (1):
k = K
ki = K / Ti
kd = K.Td
La forma de la expresión (2) es muy útil para la realización de los cálculos, ya que los parámetros aparecen de forma lineal, además de poder conseguir acciones proporcionales, integrales y derivativas puras con parámetros finitos.
Fórmulas de sintonía en lazo cerrado
Un método fundamental en la sintonía de reguladores PID, es el método en lazo cerrado propuesto por Ziegler y Nichols en el año 1942, cuyo nombre más conocido es el método de la oscilación sos-tenida. Es un algoritmo basado en la respuesta en frecuencia del proceso. Las características a determinar son:
- Ganancia proporcional crítica (Kc). Es la ganancia de un controlador solo proporcional, que provoca que el sistema sea oscilatorio (críticamente estable).
- Período de oscilación sostenida (Tc).- Es el período de oscilación que se consigue con la ganancia crítica. Las fórmulas de Ziegler y Nichols poseen reglas heurísticas, que son las siguientes:
- Las constantes de tiempo integral y derivativa se fijan en función del período de la oscilación mantenida.
- La ganancia proporcional se fija en función de la ganancia crítica.
- La constante de tiempo derivativa es igual a un cuarto de la constante de tiempo integral.
En base a ellas, las expresiones de sintonía para un regulador PID propuestas por Ziegler y Nichols se muestran en la siguiente tabla, y son función de la ganancia proporcional crítica (Kc) y del período de oscilación sostenida (Tc) del sistema en cuestión:
K = 0,6 × Kc
Ti = 0,5 × Tc
Td = 0,125 × Tc
Implementación en Matlab del método
Edición del programa
En este apartado se pretende mostrar de forma detallada un procedimiento a seguir para implementar en Matlab el método de Ziegler-Nichols en cadena cerrada para la obtención de los parámetros de un regulador PID. Para ello, se va a programar un fichero *.m, característico de este entorno, y con el cual automatizamos en la medida de lo posible las diferentes pruebas a llevar a cabo en lo sucesivo, hasta alcanzar los diferentes resultados que se pretende. El listado es el siguiente:
ng=[1];
dg=[1 6 5 0];
G=tf(ng,dg);
clf,rlocus(G);
[km,pole]=rlocfind(G)
wm=max(imag(pole));
kp=0.6*km;
kd=(kp*pi)/(4*wm);
ki=(kp*wm)/pi;
nk=[kd kp ki];
dk=[1 0];
gc=tf(nk,dk)
gd=series(G,gc)
GT=feedback(gd,1)
step(GT,’r’) %Escalón rojo para la función de transferencia con el regulador hold on
GS=feedback(G,1)
step(GS,’g’) %Escalón Verde para lafunción de transferencia sola
En la primera parte, se define la función de transferencia de la planta a la cual se le desea realizar la regulación. El siguiente grupo de instrucciones sirve para dibujar el lugar de las raíces de dicho sistema, localizando con el puntero del ratón en el (rlocfind) el punto de corte del mismo con el eje imaginario, y obteniendo en consecuencia km y wm. En el siguiente grupo se realizan las operaciones necesarias para conseguir los parámetros del regulador en la forma de la ecuación 2. Con ellos se confecciona seguidamente la función de transferencia del controlador, que se pone en serie ya con la planta, y se obtiene el sistema resultante ya con el regulador incluido. En la parte final de este script, se trazan las respuestas del sistema sin regular (en verde) y del regulado (en rojo) simultáneamente, para poder contrastar los resultados obtenidos de una forma u otra.
Ejecución del código
En este punto se muestra de forma clara la manera en la que se ha de proceder para ejecutar el código explicado en el anterior apartado, de forma que se llegue al resultado final de la presentación de la respuesta ante entrada escalón del sistema regulado, y de el sin regular.
Tras la ejecución aparecerá una figura, en la que se representa el lugar de las raíces del sistema sin controlar que se indicó al escribir el programa, tal y como se muestra en la figura 2.
Seguidamente, se lleva el puntero del ratón hasta el punto de corte del lugar de las raíces con el eje imaginario, procurando la mejor precisión posible, para lo cual se dispone de un cursor, como se ve en la figura 3. En ese punto se realizará un clic con el botón izquierdo del ratón.
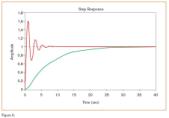
Se localizará de este modo el valor de km y de wm, con lo cual se puede obtener ya la función de transferencia del regulador, y tras lo cual se mostrará de inmediato las salidas del sistema sin controlar y controlado simultáneamente, tal y como se puede observar en la figura 4.
Ante esta respuesta se puede ver que ha cambiado notablemente con la introducción del regulador PID. Así pues, especificaciones como el tiempo de respuesta o el tiempo de establecimiento se han visto mejoradas notablemente tras la inserción del controlador. Se ve, además, que ahora existe una sobreoscilación considerable que no aparecía en el sistema inicial.
Aplicación del método para diferentes sistemas
Este método es lógicamente aplicable cuando el lugar de las raíces del sistema de partida corta al eje imaginario en algún lugar. De este modo, los sistemas que aquí se presentan cumplen esta condición.
Sistema 1
El primer sistema posee la siguiente función de transferencia:
G(S) =1 / S3+ 3S2+ 3 S + 2
Si se ejecuta el programa y se indica el punto de corte del lugar de las raíces con el eje imaginario, el resultado es el de la figura 5.
La respuesta en este caso mejora bastante, ya que las especificaciones de tiempo de pico, tiempo de respuesta y tiempo de establecimiento se ven mejoradas, eliminándose, además, el error de posición que el sistema posee en régimen permanente.
Sistema 2
Para el segundo sistema se ha seleccionado la siguiente función de transferencia:
G(S) = 1 / 0,5S3+ 6S2+ 8S
El resultado que se obtiene para este caso es el de la figura 6.
Con la salvedad del error de posición en régimen permanente que poseía el caso anterior, las especificaciones que mejoran son las mismas. En este caso el sistema regulado posee una sobreoscilación considerable.
Sistema 3
En este tercer sistema se ha seleccionado la siguiente función de transferencia:
G(S) =S + 1 / 2S3+ 3S2+ 2S + 4
El resultado que se obtiene para este caso es el de la figura 7.
En cuanto a este sistema, simplemente destacar que pasa de ser inestable a ser estable, lo cual supone una gran mejora.
Sistema 4
La función de transferencia del cuarto sistema seleccionado es la siguiente:
G(S) = 1 / S3+ 3S2+ 3S + 3
El resultado obtenido es el de la figura 8.
La respuesta obtenida no difiere mucho de ejemplos anteriores, pero en este ejemplo la sobreoscilación del sistema regulado no es tan pronunciada como en ellos.
Sistema 5
Este quinto sistema posee la siguiente función de transferencia:
G(S) = 1 / 5S + 0,5
y se le añade en serie para introducir un retardo de 0,5 segundos la siguiente función:
G(S) = –4S + 24 / S2+ 8S + 24
El resultado obtenido es el de la figura 9.
En este caso mejoran también todas las especificaciones salvo la introducción de la sobreoscilación con la adición del controlador.
Sistema 6
Este sexto sistema posee la siguiente función de transferencia:
G(S) = 25 / S4+ 5S3+ 18S2 + 13S + 1
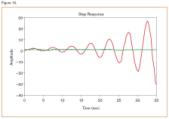
El resultado que se obtiene es el de la figura 10.
En este ejemplo la introducción del regulador PID no mejora las especificaciones del sistema, sino todo lo contrario, lo lleva a la inestabilidad. Se muestra, de este modo, que el método de obtención de los parámetros, a pesar de que el lugar de las raíces corta el eje imaginario, no obtiene buenos resultados.
Conclusión
El método de Ziegler-Nichols en cadena cerrada permite obtener los parámetros de un regulador PID con resultados muy satisfactorios en la mayoría de los casos en los que es aplicable.
Existen casos físicos en los que la aplicación de este método no es factible, debido a que es necesario llevar el sistema a la oscilación. Pero en aquellos casos en los que se pueda emplear, es muy aconsejable.
La obtención de estos parámetros para sistemas cuya función de transferencia se conoce es muy sencilla y un buen punto de partida para un posterior ajuste más fino.
Bibliografía
Ziegler, J; Nichols, N. Optimum settings for automatic controllers, Transactions of ASME, 64:759-768, 1942
Astrom, K.J.; Hagglund, T. PID controllers: Theory, Desing and Tuning ISA 2ª ed. Research Triangle Park. Améstegui Moreno, M. Apuntes de control PID. Universidad Mayor de San Andrés. La Paz (Bolivia).