Aplicación de la normativa de construcción sismorresistente

Proceso de aplicación, a través de un ejemplo de cálculo, y otras cuestiones de interés de la norma de construcción sismorresistente NCSE-02, en la actualidad vigente en España










El ámbito de aplicación de la Norma de Construcción Sismorresistente NCSE-02, así como los métodos de cálculo que indica, se refieren a estructuras de edificación.
Esta norma establece el análisis de la estructura mediante espectros de respuesta como método de referencia para el cálculo sísmico (apartado 3.6.2 de la norma), y requiere la combinación ponderada de las solicitaciones provenientes de cada modo de vibración de la construcción. También se permite el estudio dinámico por integración de los registros de aceleración (apartado 3.6.1 de la normativa).
El estudio dinámico, realizado en el dominio del tiempo o de la frecuencia, debe hacerse a partir de acelerogramas representativos del movimiento del suelo. Para ello, se requiere escalar convenientemente los acelerogramas elegidos –en el tiempo y en amplitudes– de forma que sean compatibles con la información sísmica del capítulo 2 de la norma NCSE02; en concreto lo ha de ser con el espectro de respuesta elástica y con la aceleración sísmica de cálculo. Pueden realizarse tanto acelerogramas reales modulados como artificiales, justificando en todo caso su estructura en el dominio del tiempo, su contenido en frecuencias y su duración, de acuerdo con las características del sismo de cálculo.
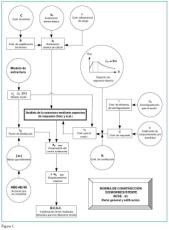
En el caso de que el técnico se decante por la primera opción, por el análisis de la estructura mediante espectros de respuesta, la secuencia de pasos que es necesario efectuar a lo largo de la aplicación de la citada normativa se indica en la figura 1. Así mismo, la aplicación de la misma se ilustra mediante el siguiente ejemplo de cálculo.
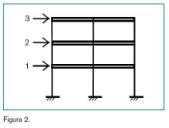
Considérese una estructura como la que se muestra en la figura 2 construida en hormigón armado, muy compartimentada, con dos ejes de simetría en planta ortogonales y con excentricidad de masas respecto al centro de torsión, inferior al 10% de la dimensión en planta. Para el citado edificio sometido a una aceleración sísmica a(t), cuyo espectro sísmico de respuesta corresponde al de la normativa española, se requiere calcular el desplazamiento máximo en cada grado de libertad.
El modelo de vibración en cada una de las dimensiones principales puede analizarse mediante dos modelos planos ortogonales independientes –y en este caso iguales– reduciendo el movimiento horizontal a un solo grado de libertad por planta (apartado 3.6.2.1 de la norma y figura 2).
La construcción se va a realizar en la ciudad de Cádiz, por lo que en función de su ubicación en el mapa de peligrosidad sísmica le corresponde (anejo 1 de la normativa) una aceleración sísmica básica ab =0.07 / g (valor característico de la aceleración horizontal en la superficie del terreno) y un coeficiente de contribución K =1.3 (coeficiente que tiene en cuenta la influencia de los distintos tipos de terremotos esperados en la peligrosidad sísmica de cada punto); para construcciones de importancia normal el coeficiente adimensional de riesgo adopta un valor unidad ?=1 (coeficiente función de la probabilidad aceptable de que se exceda la aceleración sísmica de cálculo aC en el periodo de vida para el que se proyecta la construcción).
Como se acaba de mencionar, la aceleración sísmica de diseño está dada por un mapa de peligrosidad sísmica y por una lista de poblaciones incluidas en la normativa. Su valor máximo es de 0.25 g, un valor relativamente bajo en comparación con otras regiones del globo. Sin embargo debe recordarse que el daño potencial de un sismo no solo es función de la aceleración máxima del mismo, tal como es evidente observando el tremendo daño material y humano ocasionado por el terremoto de México en 1984, con solamente una aceleración máxima del suelo de 0.2 g en la ciudad de México.
Se considera un terreno de tipo II al cual corresponde un coeficiente de suelo C =1.3 (ver apartado 2.4 y tabla 2.1 de la normativa) este coeficiente es función de la velocidad de propagación de las ondas elásticas transversales o de cizalla y pone de manifiesto la influencia de los 30 primeros metros de terreno bajo la superficie.
Para el caso en el que ?ab =0.1 g, el coeficiente de amplificación del terreno de toma el valor: 
con lo que la aceleración sísmica de cálculo alcanza la magnitud de: 
Al objeto de simplificar el análisis, se adopta para la estructura un modelo edificio simple o edificio de cortante (figura 3), con tres grados de libertad, uno por cada planta. De esta forma, las matrices de masa y rigidez son: 
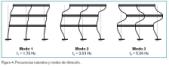
la resolución del problema característico asociado, muestra los autovalores (cuadrados de las frecuencias naturales) y autovectores (modos de vibración) correspondientes al mismo. Las frecuencias naturales (circulares o angulares) toman los valores de: 
y la representación gráfica de los mismos, se puede ver en la figura 4.
Se considera un amortiguamiento del 6.5% con respecto al crítico en cada uno de los tres modos, es decir ?1 =?2 =?3 = 0.065; ahora bien, la normativa NCSE-02 establece un espectro normalizado de respuesta elástica en la superficie libre del terreno (apartado 2.3 de la misma), para aceleraciones horizontales, correspondientes a un oscilador lineal son amortiguamiento de referencia del 5% con respecto al crítico, por lo que los valores del espectro de respuesta elástica deben de ser modificados en función del amortiguamiento.
Los periodos característicos del espectro de respuesta adoptan los valores de 
Al encontrarse todos los periodos naturales de la construcción, comprendidos entre los periodos característicos, el valor del espectro normalizado de respuesta elástica adopta el mismo valor para todos ellos (apartado 2.3 de la norma), es decir como TA =T =TB ?a(T) =2.5. Así mismo, como el periodo de cada modo es mayor que el periodo característico TA del espectro de respuesta, el valor del espectro normalizado de respuesta elástica a(T) debe multiplicarse por el factor (apartado 2.5 de la normativa)
ecuacion v=
donde ? es el amortiguamiento de la estructura expresado como porcentaje del crítico; por lo que
Modo 1
ecuacion T1=
Modo 2
ecuacion T2=
Modo 3
ecuacion T3=
Se considera que la estructura se clasifica como de ductilidad baja, por lo que el coeficiente de comportamiento por ductilidad µadopta un valor de 2. En el apartado 3.7.3.1 de la norma se recogen valores de µcorrespondientes a casos típicos.
Con los datos precedentes para ?y µ, el coeficiente de respuesta ßvale
ecuacion B=
El apartado 3.6.2.2 de la norma NCSE02 define unos coeficientes para cada modo, función de la ordenada del espectro a(T)para el periodo de cada modo considerado, del coeficiente de respuesta ßy del periodo característico del espectro de respuesta TA.
En el caso del ejemplo que se sigue, como los tres periodos naturales son mayores que TA, el coeficiente a1 adopta la misma expresión. Es decir, como
ecuacion T1 T2 T3=
utilizando esta última expresión, y teniendo en cuenta el factor de corrección ?para la ordenada espectral a(T), se obtiene para cada uno de los modos
Modo 1
ecuacion a1=
Modo 2
ecuacion a2=
Modo 3
ecuacion a3=
El factor de distribución ?ij correspondiente a la planta j en el modo de vibración i, responde a la expresión
ecuacion nij=
siendo (ver figura 2): n: número de grados de libertad (plantas).
mj: masa de la planta j que interviene en el cálculo (definida en el apartado 3.2 de la normativa).
Fij: componente del modo de vibración i en el grado de libertad (planta) j. de esta forma, para el modo 1 y el grado de libertad (planta) 1, el factor de distribución vale
ecuacion n11=
En la tabla 1 se muestra el resumen del cálculo de los factores de distribución.
Como se ha mencionado, la normativa NCSE-02 utiliza la definición de la acción mediante espectros sísmicos de respuesta y proporciona como resultado del cálculo únicamente la respuesta máxima de la estructura. Las componentes del vector aceleración asociado al modo de vibración i, correspondiente al grado de libertad j, vienen dados por
ecuacion aijmax=
con las definiciones que han sido ya vistas para cada uno de los parámetros que intervienen. Los resultados que se obtienen para cada modo son los siguientes:
Modo 1
ecuacion a1max=
Modo 2
ecuacion a2max=

Para cada dirección en que se considere la acción sísmica, los desplazamientos máximos equivalentes uijmax para el modo de vibración i, correspondiente a cada grado de libertad j, supuesto en el modelo lineal equivalente de la estructura, vienen dados por: 
siendo ?2i el autovalor (cuadrado de la frecuencia circular o angular) correspondiente al modo i. Los resultados que se obtienen para cada uno de los modos, se muestran a continuación: 
El desplazamiento modal máximo, para cada modo y cada grado de libertad (planta), se determina multiplicando el desplazamiento máximo equivalente –calculado por el procedimiento anterior– por el coeficiente de comportamiento por ductilidad µ(apartado 3.6.2.2).
La norma NCSE-02 utiliza el método de la raíz cuadrada de la suma de los cuadrados de las contribuciones modales (RCSC) para estimar la respuesta total en base a los valores modales máximos, que puede expresarse en general como 
donde S es la estimación de la respuesta (desplazamiento, fuerza, tensión, etc.) en una coordenada nodal específica, Sies la respuesta máxima correspondiente al modo i en esa coordenada y r es el número de modos que suponen una contribución significativa al resultado. 
La construcción debe resistir la acción horizontal del sismo en todas las direcciones, lo que obliga a analizarla en más de una dirección. En general basta hacerlo en dos direcciones ortogonales en planta; en este caso, las solicitaciones obtenidas de los resultados del análisis en cada dirección se combinarán con el 30% de los de la otra (apartado 3.4 de la norma NCSE-02).
La aplicación del método RCSC para combinar las respuestas modales general-mente proporciona una estimación aceptable de la respuesta máxima. Sin embargo, cuando algunos de los modos están muy próximos, el uso del método RCSC puede resultar en una substancial subestimación o sobreestimación de la respuesta máxima. En particular, se han observado mayores errores en el análisis de estructuras tridimensionales, en las cuales los efectos torsionales son significativos. El término “muy próximos” podría definirse arbitrariamente para el caso en que la diferencia entre dos frecuencias naturales sea menor que un 10% de la menor de las dos frecuencias.
Si existiesen modos de vibración cuyos periodos difieren menos del 10%, la norma NCSE-02 permite aplicar la regla anterior agrupando en una única variable Sj la suma de los valores absolutos de las variables Si que difieren entre sí menos del 10%.
Otra alternativa es recurrir al método de la combinación cuadrática completa (CCC), más preciso que el RCSC, puede considerarse como una extensión del mismo, está basado en la teoría de la vibración aleatoria y ha sido propuesto por Kiureghian (1980) y por Wilson et al. (1981).
Algunas cuestiones de especial interés
•Evidentemente, hay que considerar todos los modos que suponen una contribución significativa al resultado, y en especial todos los de periodo superior a TA (apartado 3.6.2.3.1 de la normativa).•El desplazamiento máximo para cada modo y cada planta, se calcula multiplicando el desplazamiento máximo equivalente uijmax por el coeficiente de comportamiento por ductilidad µ, es decir, el desplazamiento final de cálculo es directamente proporcional a este último, que a su vez puede adoptar alguno de los valores enteros: 1, 2, 3 o 4. Debido a la gran diferencia de resultados que se obtienen tras adoptar uno u otro, la elección del coeficiente de comportamiento por ductilidad µno es una cuestión baladí, sino que se realizará para cada modelo de cálculo (en la dirección o en el elemento analizado) dentro de las limitaciones que se establecen en el apartado 3.7.3.1 de la norma, en función de la organización estructural y de los materiales empleados, y dispondrá los detalles estructurales establecidos en el capítulo 4 de la NCSE-02 que garanticen la ductilidad adoptada.
•En lo relativo a movimientos verticales:
-Para la evaluación de la componente vertical de la acción sísmica se adoptará un coeficiente de comportamiento por ductilidad µ=1, salvo que se justifique un valor superior mediante el correspondiente análisis (apartado 3.7.3.1).
-Cuando sea preciso considerar movimientos verticales, se adoptará un espectro de respuesta elástica cuyas ordenadas espectrales sean el 70% de los valores correspondientes a las del espectro para movimientos horizontales definido en el apartado 2.3 de la norma NCSE-02. Dado que la dirección de ocurrencia de un terremoto puede ser totalmente arbitraria con respecto a la estructura, al objeto de estudiar sus efectos, normalmente la aceleración del terreno a(t) se descompone en sus componentes ax(t), ay(t) y az(t) (es decir, dos direcciones horizontales ortogonales entre sí y una tercera vertical perpendicular a las anteriores). Hasta la fecha, generalmente se ha venido prescindiendo de las acciones provocadas por las fuerzas sísmicas verticales (sin lugar a dudas debido a su desconocimiento, ya que si la magnitud de la componente vertical del sismo tiene un valor apreciable puede generar esfuerzos verticales notables), a no ser –para el caso que nos ocupa– en vigas de grandes luces y vigas ménsula. El daño observado en terremotos californianos recientes como el de Loma Prieta en 1986 y, más claramente, el de Northridge en 1994 indica que la componente vertical de los terremotos no puede ignorarse. Durante el terremoto de Northridge se midieron aceleraciones verticales mayores a la gravedad y, en general, de magnitud similar a la magnitud de las componentes horizontales. Estas observaciones seguramente modificarán la normativas de diseño americanas, por lo menos con respecto a puentes y a voladizos, donde la importancia de la componente vertical es mayor.
•En lo concerniente a las uniones:
–Cuando en el proyecto de la estructura se utilicen valores del coeficiente de comportamiento por ductilidad µ superiores a 2, las uniones se proyectarán como de resistencia total, asumiendo una sobrerresistencia de 1.2 (la capacidad de la unión será, como mínimo, 1.2 veces la de las barras unidas).
–Cuando en el proyecto de la estructura se utilicen valores del coeficiente de comportamiento por ductilidad iguales o superiores a 2, no se admitirán soldaduras de penetración parcial entre elementos críticos pertenecientes al esquema resistente a sismo. Las uniones atornilladas se proyectarán, en este caso, en forma tal que el fallo no se produzca por rotura de los tornillos.
Bibliografía
E. Balmes, Structural Dynamics Toolbox, User´s Guide (Version 3), 1997.
A. H. Barbat, J. M. Canet, Estructuras sometidas a acciones sísmicas. Cálculo por ordenador, 2a edición. Centro Internacional de Métodos Numéricos en Ingeniería, 1994.
E. Car, F. López Almansa, S. Oller, Estructuras sometidas a acciones dinámicas. Centro Internacional de Métodos Numéricos en Ingeniería, 2000.
A.K.Chopra, Dynamics of Strutures. Prentice Hall, 1995.
R.W. Clough, J. Penzien, Dynamics of Structures. Mc-Graw-Hill, 1993.
D.J. Ewins, Modal Testing: Theory and Practice. Research Studies Press Ltd., 1991.
M.A. Hacar, E. Alarcón, Elementos de dinámica aplicada a las estructuras. Edix, 1971.
A.D. Kiureghian, A response spectrum method for random vibration. Report No. UC-B/EERC-80/15, Earthquake Engineering Research Center, University of California, Berkeley, CA., 1980.
J. Moehle, Preliminary Report on the Seismological and Engineering Aspects of the January 17, 1994 North-ridge Earthquake. Earthquake Engineering Research Center, University of California, Berkeley, UCB/EERC 94/01, 1994.
M. Paz, Dinámica estructural teoría y cálculo. Reverté, 1992.
L. M. Villa García, Diseño sísmico conceptual de estructuras porticadas. Técnica Industrial, no 247, 2002.
Wilson, E. L., Der Kiureghian, A., and Bayo, E. P., A replacement for the SRSS method in seismic analysis. Int. J. Earthquake Eng. Struct. Dyn., 9, 187-194, 1981.
RESUMEN
Además de presentar la vigente normativa sismorresistente española en el campo de la edificación –a través de un ejemplo ilustrativo– el presente trabajo tiene un doble objetivo: por una parte, ayudar a los estudiantes de estructuras y construcción a vincular sus conocimientos de dinámica con la aplicación de una normativa sismorresistente, y por otra, colaborar en las necesidades de reciclaje tecnológico, de todos aquellos compañeros que, por su profesión se encuentran involucrados en el fascinante campo, del diseño y análisis dinámico de estructuras.
Luis Manuel Villa García.
villa@uniovi.es / luisma@correo.uniovi.es www.epsig.uniovi.es Técnico auxiliar – F.P. I en construcciones metálicas y técnico especialista – F.P. II en calderería en chapa estructural, ambas por la Fundación RevillaGigedo de Gijón. Ingeniero técnico industrial en Estructuras e Instalaciones Industriales por la E.U.I.T.I. de Gijón e ingeniero industrial en Construcción por la E.T.S.I.I. de Gijón. Durante algunos años desarrolla su actividad profesional en empresas dedicadas a la fabricación de transformados metálicos, bienes de equipo y montajes. Actualmente es profesor del departamento de Construcción e Ingeniería de Fabricación de la Universidad de Oviedo y participa en diversos proyectos de investigación relativos al análisis dinámico de estructuras.