Teorías de daño acumulativo en la fatiga
Diversas teorías explican el daño acumulativo en la fatiga de materiales, un fenómeno que es responsable de un 90% de los fallos de componentes metálicos de las máquinas
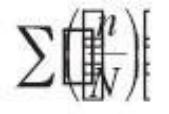
Al someter a un conjunto de probetas a solicitaciones de fatiga hasta el fallo, variando el valor de la amplitud de tensión obteníamos representando en una gráfica cuyos ejes se corresponden con la amplitud de tensión y con el número de ciclos soportados, una serie de puntos de fallo cuya curva ajustada a ellos denominábamos “Curva de Wöhler.”
La transformación de esta curva a ejes logarítmicos nos daba otra curva asimilable a dos rectas, que generalmente se denominan curvas de fatiga o popularmente cur-vas S-N , o diagramas S-N (figura 1).
Para la elaboración de estas curvas se parte de probetas sometidas a fatiga de amplitud de tensión constante. En cada ciclo completo de carga soportado por la pieza se consume parte de la vida su vida útil, cuya duración hasta su fallo es la que se pretende estimar.
En la vida real de los componentes de las máquinas la fatiga es la principal solicitación, pero estas solicitaciones no siempre son de amplitud constante, como generalmente se somete a las probetas en los laboratorios de ensayos, sino que mas bien se tratará de un espectro de cargas compuesto por la repetición de varios tipos de ciclos de carga, bien especificados en el mejor de los casos o desconocidos y aleatorios en otra gran mayoría de casos.
Aunque el concepto de daño por fatiga es fácil de comprender, su evaluación no es tan fácil, y es por lo que muchos investigadores han elaborado sus teorías cuyo objeto es evaluar el daño acumulado, según la aplicación de los ciclos de carga.
A continuación se muestran algunas de las mas significativas, sin entrar el proceso seguido por sus autores en su obtención, ya que esto sería muy extenso saliéndose del objetivo de este artículo.
Teoría de Daño Lineal o de Palmgren-Miner
Ésta fue la primera teoría de daño acumulativo. Fue propuesta por Palmgren en 1924 y desarrollada posteriormente por Miner en 1945. Conocida como Regla de Miner o Regla de Daño Lineal, es la más difundida de las teorías de fallo acumulativo, y por su sencillez es la que figura hoy en día en todos los textos de diseño de máquinas.
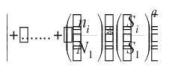
El fallo operando bajo un estado de car-gas de amplitud S1, se produce cuando se alcanzan N1 ciclos. Si el n.º de ciclos operando bajo ese estado de cargas es n1 < N1, no se producirá el fallo sino una “fracción de daño” D1.
Si se trata de un espectro de diferentes niveles de carga, se produce una fracción de daño Di, por cada uno de los diferentes niveles de tensión del espectro. El fallo de la pieza se producirá cuando se produzca el 100% de daño, es decir:
D1 + D2 + D3 +…….+DI = 1 (1)
siendo la fracción de daño:
Falta ecuacion 2
la razón entre el n.º de ciclos realizados a un determinado nivel, y el n.º de ciclos que produciría el fallo a ese mismo nivel de tensiones.
Substituyendo (2) en (1):
Falta ecuacion 1+2
Es decir:
Falta ecuacion 3
Pros: su gran sencillez, lo que explica su gran utilización.
Contras: no tiene en cuenta el orden de aplicación de los niveles de carga.
En la práctica no es independiente, pues los resultados experimentales indican que el orden en el que se aplican los distintos niveles de carga tienen una influencia significativa, y que la razón de daño a un determinado nivel de tensiones puede ser función del historial de tensiones recibido previamente.
Si se realizan pruebas en laboratorio empleando probetas sometidas a tensiones cíclicas de niveles S1 > S2 a dos grupos diferentes de forma que a uno de los grupos se le somete primero durante una relación de ciclos dada al nivel S1 y a continuación el resto de ciclos hasta el fallo al nivel S2 , los resultados de las sumas de Miner son diferentes a los obtenidos con el otro grupo de probetas en el que el orden es a la inversa.
Si primero aplicamos el nivel de tensiones S1 y seguido el nivel de tensiones S2, el resultado de las sumas de Miner:
Falta ecuacion ?
es inferior a la unidad. Si el proceso es a la inversa el resultado de las sumas es superior a la unidad. Los resultados pueden oscilar de 1/4 hasta valores de 4. Si los niveles de tensión son aleatorios, los resultados oscilan entre 0,6 y 1,6 dando entonces unos resultados aceptables. Existen varias explicaciones al respecto aunque no han sido claramente demostradas. Incluso un solo ciclo a un nivel muy alto de tensión puede tener una gran influencia en el fallo por fatiga.
Si dibujamos la fracción de daño en función de la relación del n.º de ciclos n/N, según esta teoría de P-M, nos dará una recta 2, según la figura 2.
Si nos basamos en resultados experimentales, vemos que aparecen “no linealidades” como indican las curvas 3 y 1. La curva 1, si los niveles de amplitud son mayores y la curva nº 3 si los niveles de amplitud son inferiores.
Por ejemplo: Una relación de daño D = 0,4 se obtendría según P-M con la relación de ciclos n/N = 0,4. Esta relación de ciclos produciría una fracción de daño de 0,78 bajo las condiciones de carga de la curva 1 y una fracción de daño de 0,08 bajo las condiciones de carga de la curva 3.
Varias teorías se han propuesto para aproximar la no linealidad en la relación entre “fracción de daño” y “relación de ciclos”. Se enuncian algunas a continuación:
Teoría de Marco-Starkey
Una de las primeras teorías no lineales de daño acumulado fue propuesta por Marco y Starkey en el año 1954. Una teoría similar fue propuesta por Richart y Newmark.
La teoría de Marco-Starkey se basa en tres postulados:
1.º Las curvas de daños para cada nivel de tensiones sinusoidales completamente alternadas viene definido por:
mi: es una función del nivel de tensiones.
2.º El fallo se producirá cuando D = 1.
3.º El fallo o daño 100% se alcanzará cuando
sea igual a un valor crítico,que se obtiene mediante una expresión compleja de datos experimentales.
Con la figura anterior podemos ilustrar esta teoría que relaciona la razón de daño (D) con la relación de ciclos (n/N) para tres niveles diferentes de tensiones.
Consideramos dos secuencias de tensiones s1 y s3.
1ª secuencia: Aplicamos primero s1 con una relación (n/N) = 0,5 y después aplicamos s3 hasta D = 1 (fallo).
2ª secuencia: Aplicamos primero s3 hasta una relación (n/N) = 0,5 y después s1 hasta que D = 1 (fallo).
En la primera secuencia cuyo camino seguido es OMNF (figura 3):
En la segunda secuencia cuyo camino es OABF:
Observamos que la relación de ciclos es inferior a la unidad, cuando la carga mayor se aplica primero y viceversa, estando de acuerdo con los valores experimentales de laboratorio.
Primeramente se deben dibujar las cur-vas de daño con respecto a la relación de ciclos, como se ve en la figura 4, cuya relación empírica se da en (4). Después se establece la secuencia de operación y se lleva a la gráfica con líneas de cambio horizontal (daño cte.) hasta alcanzar la fracción de daño unidad.
Teoría de Henry
Fue desarrollada por Henry en el año 1955 y se basa en el concepto de que la curva SN debe ajustarse como daño por fatiga acumulado y que el daño por fatiga debe definirse como la relación entre la reducción en el límite de fatiga respecto al límite de fatiga original o de la pieza virgen, es decir:
D : daño
E0 : límite de fatiga original
E : límite de fatiga después del daño.
Henry asume además que la curva S-N del material virgen podría representarse por la ecuación de un hipérbola equilátera referida al eje de tensiones y una línea pasando a través de Eo paralela al eje de ciclos como asíntota de la hiperbola.
Entonces la ecuación asumida tiene la forma:
N : nº de ciclos
S : amplitud de las tensiones aplicadas completamente invertidas
K0 : cte de material
E0 : límite de fatiga original
Este desarrollo implica que no hay acumulación de daño por operar a niveles de tensiones cíclicas bajo el límite de fatiga.
Henry asume además que la curva S-N después del daño pudiera también representarse por otra hipérbola equilátera:
Nr : n.º de ciclos remanentes hasta el fallo a tensiones de amplitud S
S : amplitud de tensiones completamente invertidas
K : cte de material
E : límite de fatiga acumulada (reducida desde E0)
Examinando datos y haciendo algunos argumentos heurísticos Henry afirmó que es aproximadamente cierto que:
Si n ciclos de tensiones de amplitud S se aplican a una muestra, la vida remanente es Nr = N-n , siendo N, el n.º de ciclos requeridos para producir el fallo del material virgen cuando esta sujeto a amplitudes de tensión S.
Sustituyendo en (7) tendremos:
Dividiendo por N y sustituyendo por su valor de (6)
Expresión que nos da el valor actual del límite de fatiga tras n ciclos aplicados de tensión completamente invertida S, si el n.º total de ciclos para el fallo era original-mente N al nivel de tensiones S y el límite de fatiga original fuera E0.
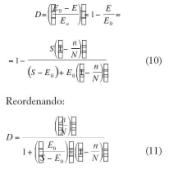
Esta expresión puede convertirse en ecuación de daño sustituyendo este valor nuevo de E en la expresión (5) :
S: amplitud de tensiones aplicadas.
n: n.º de ciclos aplicados a la amplitud de tensión S.
D: fracción de daño.
Esta teoría puede extenderse a una secuencia de diferentes niveles de tensión aplicando las expresiones (10) u (11) sucesivamente en el mismo orden que las tensiones. El valor E0 deberá ser actualizado después de cada aplicación de cada amplitud de cargas E0 , E1 , E2 ,…
E0 : límite de fatiga original.
E1 : límite de fatiga tras aplicar el primer nivel de tensiones S1 durante n1 ciclos.
E2 : límite de fatiga tras aplicar el segundo nivel de tensiones S2 durante n2 ciclos.
etc….
Una modificación usual de la Teoría de Henry implica que pasen todas las curvas S-N a través de (Su, para 1 ciclo) y conectando este punto con el valor E obtenido en (9) para 106 ciclos, por una línea recta en escala semilogarítmica (S-logN) para obtener la curva S-N completa a cada nivel de daño.
Teoría de Corten-Dolan
Esta teoría se basa en 6 suposiciones que al menos cualitativamente están contrastadas por datos. Estos supuestos son:
1.º Para iniciar el daño permanente a fatiga se requiere un período de nucleación, (generalmente un pequeño número de ciclos).
2.º El número de núcleos dañados (vacíos submicroscópicos) que aparecen en todo el elemento se incrementa igual que se incrementa la tensión.
3.º El daño para una amplitud de tensiones dada, se propaga con una razón incremental a como lo hace el nº de ciclos.
4.º La relación de daño por ciclo aumenta como aumentan las tensiones.
5.º El daño total que constituye el fallo en una pieza determinada es una constante, para todos los posibles historiales de tensión que pudieran ser aplicados.
6.º El daño continuará propagándose a niveles de tensión inferiores al mínimo requerido para iniciar el daño.
Para simplificar el desarrollo Corten y Dolan asumieron que inicialmente el periodo de nucleación fuera cero. (N´ = 0) donde N´ es el número de ciclos bajo tensión S que se requiere para nuclear el daño.
Se asumió una ley para relacionar el daño por núcleo con los ciclos aplicados:
D´ = r · Nª
D´: daño por núcleo
r: coefte de propagación de daño en función del nivel de tensión
a: exponente de propagación del daño
m: n.º total de núcleos dañados.
N: n.º de ciclos de tensión correspondientes al daño.
Para ilustrar esta teoría suponemos un historial de 2 niveles de tensión en bloques de ciclos como se indica en la figura 5.
S1 : amplitud de mayor valor
S2 : amplitud de menor valor
nr : n.º total de ciclos en cada bloque de repetición
a: fracción de los nr ciclos correspondiente al nivel superior S1
Corten y Dolan desarrollaron una expresión basándose en las 6 suposiciones prescritas para estimar el n.º de ciclos hasta el fallo, para bloques repetidos de diferentes niveles de tensión.
(Ng)f: n.º total de ciclos hasta el fallo
d: constante de material
N1: Ciclos hasta el fallo para el nivel alto de tensiones S1
a1, a2, .. ai: fracción de ciclos impuestos a los niveles de tensión S1, S2,..Si
El valor de “d” debe obtenerse experimentalmente, para cada material de interés . Corten y Dolan obtuvieron para alambre de acero aleado de 1/20” de diámetro un valor medio de d = 6,57 estando los valores extremos entre 6,2 y 6,9. El valor medio para el aluminio aleado 7075-T6 fue de d = 6,0.
Dibujando el daño respecto al número de ciclos aplicados para los dos niveles de tensión según la teoría de Corten-Dolan,se representa en la figura 6:
A efecto de comparación con la teoría posterior de Marín, la expresión puede transformarse teniendo en cuenta que:
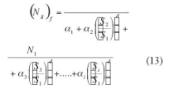
a1nr + a1nr + a1nr + …. + a1nr = nr
si “g” es el n.º de veces de repetición del bloque: g*nr = Ng n.º total de ciclos en todo el historial impuesto. Multiplicando por “g” en ambos miembros:
que es lo mismo que poner la suma de la totalidad de ciclos de cada nivel:
n1 + n2 + n3 + … + n1 + = Ng
Si dividimos (13) en ambos miembros porNg
Teoría de Marín
La teoría de Marín se basa en considerar la relación entre el daño como función de la relación de ciclos, y los cambios de la curva S-N debido a la acumulación de daño.
Si graficamos las curvas de daño obtenidas experimentalmente para varios niveles de tensión como se muestra en la figura 7, podemos seleccionar una línea de daño constante p.ej.: D = 0,4 cada punto (1,2,…..7) se corresponde con ese nivel de daño para las 7 curvas de diferentes niveles de tensión dibujados (S1,S2,…..S7 )
El concepto de curvas S-N de daño constante como se muestra en la figura 8, nos lleva a la observación que el daño producido a ni ciclos de operación a cualquier nivel de tensiones Si es exactamente equivalente a n1 ciclos de nivel de tensión S1 donde n1, n2 ….ni son todos puntos de la curva de daño constante.
Es posible por tanto encontrar un n.º equivalente de ciclos a un nivel de referencia que produzca el mismo daño que ni ciclos de operación al actual nivel de tensión Si .
Usando este concepto y seleccionando como nivel de tensiones de referencia el mayor (S1) Marín desarrolló la expresión:
que coincide con la desarrollada por Corten y Dolan si el exponente “y” de Marin se hace igual a exponente “d” de Corten-Dolan.
La expresión de Marín fue aún más desarrollada, asumiendo que las curvas S-N podrían representarse aproximadamente con la expresión:
haciendo lo mismo con todos los niveles y llevando cada uno a su correspondiente sumando de la ecuación (15), nos da:
donde q = y – x
se hace notar que si y = x, q se hace cero, coincidiendo entonces la teoría de P-M.
Con la expresión (16) podemos predecir el fallo bajo condiciones de espectros de carga si conocemos la constante del material “q” y la curva S-N del material virgen.
Si estamos interesados en la vida remanente a un nivel de tensiones Si, después de haber operado bajo algún espectro conocido de cargas, podemos obtenerla despejando de la ecuación anterior:
donde :
nir: es la vida remanente en ciclos al nivel de tensiones Si después de haber aplicado n1 ciclos a la tensión S1, n2 ciclos a la tensión S2 ,…. ni-1 ciclos a Si-1.
Basándose en datos experimentales de muchos materiales diferentes estableció el valor p = 0,6. Para espectros de dos niveles de tensión el coeficiente de propagación encontrado experimentalmente fue P = 14.
Experimentación adicional condujo a Manson a restringir estas ecuaciones a un rango de tensiones Nf superior de los 730 ciclos, puesto que en períodos de vida inferiores a este número de ciclos parecía ocurrir que la formación de la grieta se producía en el primer ciclo de tensiones, puesto que la vida total Nf estaba justamente asociada con la fase de propagación. Por tanto:
Con estas expresiones empíricas aplicamos la regla de fallo lineal a cada fase individualmente para predecir la iniciación y el fallo.
El tamaño crítico del núcleo de fatiga se inicia cuando:
y la grieta se propaga hasta el fallo si el tamaño crítico de la grieta ha sido iniciado antes, y entonces:
n: n.º de ciclos aplicados al nivel i-ésimo o j-ésimo de tensiones.
Debemos aplicar (21) hasta que sea iniciada una grieta crítica y después aplicar (22) hasta que se preduce el fallo.
El uso de esta regla bilineal de daño parece dar buenos resultados con las pruebas llevadas a cabo con dos niveles de tensión y con varios materiales.
Las siguientes gráficas de la figura 9 muestran los resultados experimentales de las pruebas hechas con acero SAE-4130 comparando las hipótesis de Man-son con las de Palmgren-Miner para diferentes espectros de dos niveles de tensión.
Sus recientes esfuerzos ahora están basados en definir mas concretamente el comportamiento durante los ciclos de iniciación y propagación N´ y Np respectivamente llamándose también fases I y II, y desarrollando una curva expresada como “curva ajustada al doble daño”.
Ejemplo
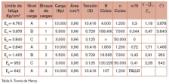
Se desea determinar el área de la sección circular de una barra de Acero AISI-4340 tratado hasta una dureza de 35 Rockwell-C, para soportar cargas axiales cíclicas total-mente invertidas, cuyo espectro es:
PA= 10.000 Kp durante 1.200 ciclos
PB= 5.500 Kp durante 7.000 ciclos
PC= 3.000 Kp durante 50.000 ciclos
El espectro de cargas deberá repetirse 3 veces durante la vida de la barra.
Calcular para una probabilidad de supervivencia de 99% empleando las teorías de fatiga acumulada.
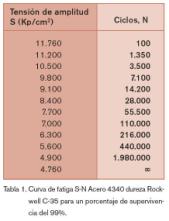
La curva S-N de fatiga para este acero sometido a cargas cíclicas totalmente invertidas se da en la tabla 1:
Sy : 11.060 Kp/cm2 ; Su = 11.760 Kp/cm2
Partimos de una sección transversal supuesta de 1,30 cm2.
El valor de las tensiones máximas para cada uno de los tres niveles:
Teoría de Palmgren-Miner
1ª Iteración. A=1,3 cm2 (figura 10)
2ª Iteración. A=1 cm2
3ª Iteración. A=0.96 cm2
Teoría de Henry
Partiremos del área obtenida por Palmgren- Miner A = 0,96 cm2 y mediante la ecuación:
obtenemos la tabla 5:
El fallo se ha producido en el primer nivel de cargas del tercer bloque, por realizar sólo 107 ciclos de los 1.200 que debería hacer. Lógicamente habría que aumentar el área para que en el nivel de carga C del tercer bloque, N valga 50.000 que son los ciclos que tendría que realizar dando n/N = 1
Teoría de Corten-Dolan
La expresión utilizada es:
alcanzando el fallo cuando D = 1
Considerando el mismo área A = 0,96 cm2 y una constante de material media d = 6,57 tenemos para la 1ª iteración:
Lo cual nos hace ver que justamente fallaría al aplicar el último nivel del tercer ciclo, aunque para tener la certeza de que lo supera, deberíamos aumentar muy ligeramente el área.
Teoría de Marín
Se basa en la ecuación:
Siendo la constante del material : q = y – x
El valor de “y” coincide con el valor “d” de Corten-Dolan: y = 6,57
El valor de “x” lo debemos sacar por la tangente de la recta S-N en ejes logarítmicos.(Figura 11)
Asumimos el área A= 0,96 cm2
Al igual que la teoría anterior el fallo ocurrirá justamente al final de la aplicación del tercer bloque de cargas, por lo que el área de la barra debería ser ligeramente incrementado.
Teoría bilineal de Manson
Las ecuaciones empleadas por Manson son:
El tamaño crítico de la grieta del núcleo de fatiga se ha alcanzado, (es decir la grieta ya se ha formado o incubado) si
y el tamaño de la grieta se propaga hasta el fallo si se ha producido el tamaño crítico de núcleo y se produce
Asumimos el área A=0,96 cm2
Observamos que para el nivel mas alto de tensiones (10.416 Kp/cm2) del espectro, la curva S-N del material nos la da Nf = 4.000 > 730 ciclos, por lo que empleamos las 1ras ecuaciones. Idénticamente para los otros dos niveles de carga (tabla 6).
Observamos que bajo el Nivel de car-gas A, serían necesarios 4.000 ciclos para alcanzar el fallo, de los cuales 2.030 serían de propagación de grieta, por lo que para incubarse la grieta hubieran sido necesarios 4.000-2.030 = 1.970 ciclos. Como bajo este estado de carga inicialmente sólo debe realizar 1.200 ciclos quiere decir que empezará con el segundo nivel de cargas sin haberse incubado la grieta.
Para el segundo nivel de carga se necesitarían 398.000 ciclos para el fallo, de los cuales se emplearían 365.933 ciclos de incubación y el resto, 32.066 ciclos de propagación hasta la rotura.
En el tercer nivel de carga, al estar sometido a un estado tensional inferior al límite de fatiga, nunca se incubaría una grieta y por tanto tampoco se propagaría.
Calculamos ahora, cuándo se produce el tamaño crítico de grieta o “microfisura”.
1ª Iteración de formación de grieta (tabla 7):
Vemos que el núcleo de grieta o microfisura se ha creado durante el 1er nivel de carga (A) del 2do bloque en que S(n/N) ha sobrepasado la unidad.
Para determinar exactamente en qué ciclo del nivel A del bloque 2 se ha iniciado la grieta:
luego quedan 1.200 – 733 = 467 ciclos de ese nivel en el que la grieta se propaga.
1ª Iteración de propagación de grieta (tabla 8):
Vemos que el fallo se ha producido en el nivel A del tercer bloque de cargas, por lo que el área debería aumentarse.
Para determinar en qué ciclo del nivel A se ha producido el fallo:
Conclusiones
En la mayor parte de los casos se sigue empleando la teoría lineal de Palmgren-Miner, limitándose el empleo de las demás, fundamentalmente a laboratorios especializados y de investigación.
En la actualidad se sigue investigando, en cada una de las cinco etapas en que se ha establecido el fallo por fatiga, de las cuales las tres primeras corresponderían a la llamada Fase-I o de creación de grieta referida antes (la velocidad de propagación es muy lenta) y las dos últimas a las Fases-II y III respectivamente, de propagación apreciable de la grieta, a saber:
1. Etapa de nucleación: aparición de una microfisura.
2. Etapa de propagación de las microgrietas hasta el tamaño del nivel del grano. (en esta propagación no sirve la teoría de mecánica de la fractura, sino otras teorías de tipo metalúrgico).
3. Etapa de crecimiento de las microgrietas hasta grietas cortas (se emplearían teorías elastoplásticas, por ser así la zona donde se produce este crecimiento).
4. Etapa de crecimiento de grietas largas. (aplicación de las teorías de mecánica de la fractura conocidas). El crecimiento se ajusta en la mayoría de los casos a la denominada Ley de Paris:
da/dN = C(?K)n
donde ?K representa el rango del factor de intensidad de tensiones da/dN la velocidad de propagación de grieta por ciclo y C y n son constantes características del material
5. Etapa de propagación inestable. La velocidad de propagación aumenta rápidamente y tras sobrepasar un tamaño crítico, se entra en proceso de crecimiento repentino y descontrolado.
Podemos destacar que en componentes pequeños y con materiales tenaces, antes de alcanzarse esta condición, la sección remanente puede presentar el colapso plástico, en cuyo caso la naturaleza del fallo final sería distinta a la arriba indicada.
Bibliografía
J.A.Collins “Failure of Materials in Mechanical Desing: Analysis, Prediction, Prevention.” 2ª Edición. Editorial Wiley Inter Science. 1993
X.Ayneto “Analisis de fatiga y durabilidad a partir de prototipos virtuales” (Marzo 2000). ST Mecánica Aplicada, S.L.; http://www.stmecanica.com
D.F. Socie. “Multiaxial Fatigue”. Editorial SAE International. 2000
J.E. Shigley “Diseño en Ingeniería Mecánica” 5ª Edición.Editorial McGraw-Hill. 1990
Robert C. Junivall “Fundamentos de Ingeniería Mecánica.”. Editorial Limusa. 1993
A. Fatemi; L. Yang “Cumulative Fatigue Damage and Life Prediction Theories: A Survey of the State of de Art for Homogeneous Materials”. International Journal of Fatigue . Vol. 20, Nº 1, 1998
RESUMEN
El movimiento es inherente a las máquinas, puesto que a éstas cada vez se les exige mayores prestaciones, también mayores son los movimientos relativos de sus componentes, así como también lo son las solicitaciones a que están sometidos. De las tensiones continuamente cambiantes surge el fenómeno de la fatiga como solicitación principal y causa de fallos en el estudio y diseño de los componentes de las máquinas, motivo por el cual la validación y homologación de los componentes mecánicos son relativos a ensayos de fatiga. Las técnicas de análisis por elementos finitos dentro de los procedimientos de simulación por ordenador permiten simular de forma rápida estos ensayos en el diseño, que será muy probablemente definitivo y que superará por tanto los ensayos reales (con gran probabilidad de éxito). En este artículo se presentan algunas teorías de daño acumulativo, o del consumo de vida que suponen los casos de carga en los que la amplitud de la tensión no es constante, como se supone generalmente en los estudios de fatiga simulados por ordenador.









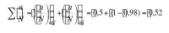
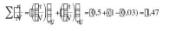





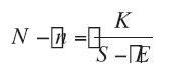

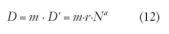

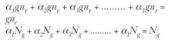


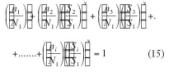
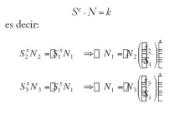
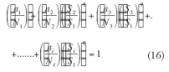

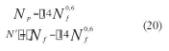


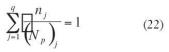

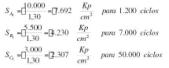
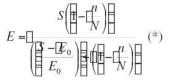







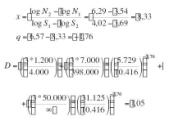
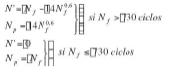
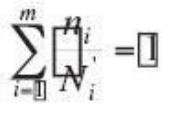 46
46 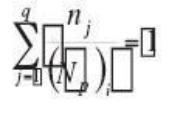 47
47 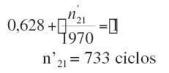 48
48 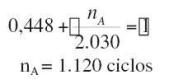 49
49 