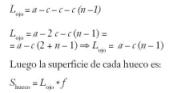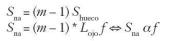Ventilación natural mediante rejillas
El diseño de las rejillas es un factor a tener en cuenta para adaptarse a la normativa sobre aireación de los locales y estancias
Algunos reglamentos y normas aceptan la ventilación natural directa como medio de ventilación de un local o estancia. Por ejemplo la MI BT ITC 29 (RD 842/2002) sobre instalaciones con riesgo de explosión o incendio, da la posibilidad de desclasificar el emplazamiento mediante la ventilación natural directa. El nuevo reglamento de gas RD 919/2006 admite para salas de calderas la ventilación natural directa, así como para cocinas o locales con aparatos de gas de combustión (o cámara de combustión) no estanca. El derogado RIGLO también daba esta posibilidad así como el RITE también contempla esta posibilidad para ventilar la sala de calderas, y aportar el oxígeno necesario para la combustión. De igual modo, el Reglamento de Alta Tensión menciona la ventilación natural para los locales que albergan los transformadores, el DB S.I del CTE también habla de la ventilación natural para los garajes, y lo mismo hacía la derogada NBE CPI 96. Por tanto, no es baladí el dimensionamiento y la ejecución de este tipo de ventilación, pues un dimensionamiento erróneo o una mala ejecución de estas ventilaciones puede acarrear explosiones y hasta la muerte de personas y animales.
Normalmente la superficie en contacto permanente con el aire exterior exigida por los reglamentos o normas, suele ser un porcentaje de la superficie del local o un porcentaje del volumen del local considerado. Por ejemplo la Instrucción 3/2005/RSI. de la Junta de Castilla y León, sobre instalaciones eléctricas en garajes, acepta una superficie de ventilación natural directa de 0,5% de la superficie construida del garaje. Ha de entenderse de superficie en contacto permanente con el aire exterior.
Es habitual que para el cálculo de esta superficie se tenga en cuenta el hueco neto de la ventana: no se descuentan lo que ocupa el marco, los nervios o las propias lamas que conforman la rejilla. Todas estas superficies han de descontarse del hueco neto de la ventana. Descontar el espacio que ocupan los marcos y los nervios de la rejilla es muy fácil, lo que ocupan las lamas de las rejillas es un poco más laborioso, sobre todo porque casi nunca se sabe qué tipo de lama es la que se monta. Los fabricantes de los perfiles que se usan para las lamas no suelen tener tabulados los valores de superficie frontal, así que no nos queda más remedio a los proyectistas que buscar en catálogos (si los hay de los perfiles), o bien preguntarle al constructor, al promotor, al arquitecto qué tipo de lama se monta. En raras ocasiones el ingeniero decide qué tipo de lama se monta y la separación entre ellas, para así de esta manera asegurar que la superficie del local en permanente contacto con el ambiente exterior es la mínima exigida.
La forma de la lama y el número de ellas es fundamental. Veamos un ejemplo.
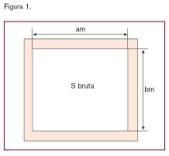
Supongamos una ventana del tipo de la figura 1.
Superficie bruta de la ventana:
Sbruta= a m× bm
Ahora, en base a este hueco de ventana, se fabrica la rejilla que está formada por el marco, los nervios centrales, si existen, y las lamas.
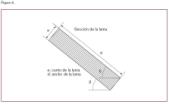
Suponemos que las lamas están fabricadas con pletina o una llanta.
El ángulo con el que se monta la pletina sobre los marcos es decisivo para determinar la superficie neta en contacto permanente con el ambiente exterior.
Como caso general, supongamos una rejilla con n ojos, luego el número de nervios intermedios es n-1 y que la interdistancia entre nervios es idéntica.
Puesto que la rejilla está inmersa en un fluido (el aire), suponemos que la presión estática es igual a todos los puntos de la lama y por tanto entra perpendicular al eje de magnitud f. Pues conocido el largo del ojo de la rejilla:
Como se ha dicho, hemos supuesto que la distancia “f” se mantiene constante para todas las lamas, lo que sólo facilita el cálculo. Si no fuera igual, la distancia que no está en un lado estará en otro.
Luego si tenemos m lamas existen m – 1 huecos, por lo tanto la superficie neta total en contacto con el aire:
luego vemos cómo S es directamente proporcional a la magnitud f, pero ocurre que f = g(ß), siendo ß el ángulo indicado en la figura 3
Superficie que tapa (que obtura el ojo de la rejilla) la rejilla para un ángulo ß
Conclusión
Vemos pues, que cuando el ángulo ß = 0, el espacio que ocupa la lama dentro del ojo de la rejilla es el menos posible; sin embargo, cuando ß = 90, la superficie ocupada por las lamas es la mayor posible.
Con este ejemplo tan sencillo, se demuestra que para una rejilla tipo, el ángulo ß es decisivo, de tal guisa que puede darse el caso de que la superficie de ventilación cumpla con la mínima exigida, o no cumpla.
Una situación ideal es aquella en la que el fabricante de la rejilla preguntara al proyectista la superficie en contacto directo con el ambiente exterior, y esto a su vez se reflejara de manera indeleble en la rejilla.