El coeficiente ß de pandeo en pórticos triarticulados de madera laminada: una propuesta de ecuación mediante el m.e.f.
Introducción
Los tres materiales más empleados en construcción son el hormigón armado, el acero y la madera, siendo los dos primeros los más generalizados. Si bien, es cierto que en las últimas décadas está cogiendo un notable auge el empleo de estructuras de madera tanto laminada como aserrada.
La diferencia fundamental entre la madera aserrada y laminada es que en la última, y debido al proceso de fabricación, se minimizan los defectos naturales del material. Esto es así porque, una vez que se tienen las láminas de bajo espesor (del orden de 32-38 mm y con frecuencia de Picea abies o falso abeto), se encola bajo presión con colas estables bajo ambientes agresivos o a la intemperie. La unión de láminas encoladas introduce la posibilidad de obtener piezas de diversas formas y longitudes, lo que per-mite alcanzar grandes luces sin mayor problema. Una vez fabricadas las vigas, si el material se trata adecuadamente se puede considerar como prácticamente inalterable a agentes químicos y temperaturas extremas, lo que permite su uso a la intemperie en interiores, etc.
La propiedad física más importante de la madera es la densidad, que depende de la especie, siendo para las coníferas usadas en construcción (como en el abeto, pino, etc.) un valor entre los 400 y 550 kg/m3 y para las frondosas (roble, haya, etc.) entre 600 y 700 kg/m3.
El valor relativamente bajo de la densidad de la madera en comparación con su resistencia y módulo de elasticidad convierte a la madera en un material especialmente adecuado para aplicaciones estructurales. Se puede advertir que las soluciones constructivas clásicas en madera resultan más ligeras que las del acero y mucho más aún que las de hormigón.
Con la ligereza de la estructura se consigue disminuir una de las cargas que afectan a la estructura y a la cimentación, el peso propio, con lo que aporta una ventaja importante en estructuras de grandes luces. Se puede añadir a este bajo peso propio que aporta que podamos emplear estructuras isostáticas con más facilidad, lo que supone una solución muy válida para suelos de escasa capacidad portante por sus menores cimentaciones. Se concluye entonces que el empleo de las estructuras de madera laminada, económicamente hablando, se encuentra en las grandes luces y sobre todo en grandes luces combinadas con suelos de baja calidad.
A las características mencionadas hasta ahora deben añadirse otras de índole no estructural como su facilidad de in tegración en entornos naturales y no naturales por el escaso impacto visual e imagen de nobleza de su estructura. La madera actúa también como aislante a todos los niveles: acústico, térmico, eléctrico y magnético, logrando espacios confortables y seguros.
Estas circunstancias hacen de la madera un material muy interesante en algunas soluciones estructurales que se establecen en las fases de diseño de pabellones deportivos, iglesias, piscinas cubiertas, centros comerciales (mezclado con hormigón), mercados de ganado, recintos feriales y de exposiciones, pasarelas fluviales, viviendas rústicas, bodegas, superficies industriales, etc.
Descripción del problema
En la actualidad las estructuras de madera laminada que se emplean en el caso de grandes luces son casi siempre isostáticas, arcos triarticulados y pórticos triarticulados, pues se facilita el transporte a su ubicación definitiva con grandes dimensiones y porque se eliminan así los posibles esfuerzos internos que se gene-ran ante variaciones de dimensiones debidas a la humedad, etc.
Es muy habitual, por tanto, el arco triarticulado pero también el pórtico triarticulado en las bases y unión de vigas.
El cálculo de estas estructuras se realiza basándose en las estipulaciones del Documento de Seguridad Estructural Madera (DB SE-M) del Código Técnico de la Edificación1 y también aen el Eurocódigo 5 “Proyecto de estructuras de madera” Parte 1-1. Reglas generales y reglas para la edificación2.
En ambas normas, por medio del parámetro esbeltez y al igual que en todas las normas de construcción, se introduce la influencia del pandeo en función del coeficiente ß de pandeo, que debemos calcular para nuestro pórtico concreto. Es conclusión inmediata que el coeficiente de pandeo es un parámetro necesario en la comprobación de pórticos triarticulados de madera y es en este punto donde debemos añadir que en madera, debido a la deformabilidad de las uniones, estos coeficientes que tienen valores teóricos de ß = 1 para la columna de Euler, 2 para la empotrada libre, etc. se deben incrementar en este tipo de estructuras entre un 15% y un 50%.
Métodos de proyecto para la estimación del coeficiente de pandeo
El valor del coeficiente de pandeo no depende del material que se emplea, y por tanto cualquier método es válido para acero, hormigón o madera. En la actualidad las normativas europeas y españolas de acero y hormigón ofrecen los métodos de Wood y Julian-Lawrence3 respectivamente para la estimación del coeficiente ß de pandeo en pórticos ortogonales de varias alturas, formados por barras de sección constante. Los dos métodos, que ofrecen resultados similares, tienen cierta aplicación en los pórticos de una altura siempre que las articulaciones estén en las bases de los pilares y no en la unión entre barras.
Las normas DIN ofrecen métodos de cálculo de ß para pórticos de una altura por medio de ecuaciones sencillas que ajustan el resultado de otras ecuaciones, en las que aparece ß de forma implícita, consecuencia de calcular la carga crítica tras la integración de las ecuaciones de equilibrio. De todas las normas DIN, la de aplicación para los pórticos triarticulados es la DIN 1052, que en la práctica es el método que se está empleando para calcular el coeficiente de pandeo de los pórticos triarticulados que aquí se analizan.
Todas estas fórmulas presuponen la actuación única de cargas puntuales en los pilares de forma que las vigas o dinteles trabajan en ausencia de axil y no es posible la flexión de ninguna barra antes de que se produzca el pandeo. Sin embargo, la realidad de las cargas (peso propio, nieve, etc.) implica un conjunto de cargas puntuales debidas a cada correa que asumimos en global como cargas uniformemente distribuidas, lo que no deja de ser una adecuación o simplificación de la realidad a nuestro proyecto.
Esta simplificación implica tener unos valores del coeficiente de pandeo inferiores a los que obtenemos considerando la carga tal y como es y por tanto nos dispone del lado de la inseguridad.
Tras estos antecedentes, surge la necesidad de estimar el valor de este coeficiente de pandeo para la hipótesis de carga más desfavorable en la mayoría de los casos: carga permanente, uso y nieve, que responde a una carga uniformemente distribuida4.
Método de análisis empleado
Todos los resultados que van a aparecer a continuación han sido obtenidos mediante el método de los elementos finitos usando el paquete comercial ANSYS. Para el análisis de pandeo, se ha usado un método lineal de estimación de modos de pandeo, el pandeo linealizado, que simplifica la matriz de rigidez tangente al no considerar la matriz de grandes desplazamientos de manera que se pueda obtener un resultado lineal con un bajo coste computacional. De esta forma, analizamos el fenómeno del pandeo como un problema de extracción de autovalores cuyos autovectores asociados manifestarán las formas modales de pandeo5.
Se han empleado elementos de viga “Beam3” (según la nomenclatura de ANSYS), que corresponden a elementos de viga en dos dimensiones empleando los postulados de la flexión de Timoshenko.
Generación y validación de los modelos paramétricos
En este trabajo se busca avanzar en el desarrollo de los modelos de un modo progresivo abordando la siguiente etapa tras haber validado y asegurado en la fase anterior la veracidad del resultado. Esta fase es una de las más importantes del estudio en cuanto que se discuten situaciones relativas al tipo de modelización, y se validan los resultados de manera que podemos llegar a parametrizar los pórticos de estudio sobre la base de sus características principales.
Las fases de la generación fueron:
1. Modelización y validación de la columna de Euler.
2. Modelización y validación de la columna empotrada-libre
3. Modelización y validación del pórtico biempotrado: confrontación con el resultado de la ecuación diferencial y norma DIN
4. Modelización y validación de pórtico biarticulado
5. Modelización y validación de pórtico triarticulado de madera con cargas puntuales
6. Modelización del pórtico triarticulado de madera con cargas uniformes: comienzo de la fase de investigación propiamente dicho.
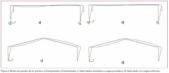
De todas ellas se desglosa aquí la fase 6 y se ofrecen los modos de pandeo de las diversas fases intermedias en la figura 2.
Así, en la fase 6 se analiza el pórtico triarticulado con cargas verticales uniformes sobre los dinteles. En este punto de la investigación sólo nos falta someter al pórtico a cargas uniformes para estimar así el coeficiente de pandeo ob jetivo.
Es en esta fase además en la que se parametrizan todas las variables del pórtico, de forma que tengamos una facilidad de trabajo importante, circunstancia que resulta clave de cara a la investigación.
Si calculamos el pórtico anterior, se obtiene un resultado del coeficiente de pandeo ß=3,9829, valor que difiere del de la norma DIN 1052 en un 13,93%.
Es importante destacar que para este pórtico concreto ésta sería la diferencia del lado de la inseguridad que estaríamos permitiendo al diseñar este pórtico con la ecuación de la norma DIN. Algo que es esperable y coherente por la pérdida de rigidez del dintel debida a la influencia del axil que no se tiene en cuenta en las ecuaciones de la norma DIN.
En la figura 2.d se puede observar en la forma modal de pandeo del pórtico.
Análisis de tendencias de las variables
Desde un punto de vista práctico surge la necesidad de conocer la evolución del coeficiente de pandeo ß en función de las variables que afectan a su valor. De esta manera se consigue realizar un estudio más eficiente que permitirá centrarse en los aspectos de mayor relevancia, así como aportar una gran información para afrontar cualquier toma de decisiones que pueda influir en dicho coeficiente ß.
Las variables que afectan al coeficiente ß de pandeo para un estado de carga dado son aquellas que definen un pórtico:
1. La altura de los pilares.
2. La luz del pórtico.
3. La pendiente de los dinteles.
4. Las relaciones geométricas entre pilares y dinteles.
Como resumen del análisis de tendencias, se observó una fuerte influencia de las proporción luz-altura y proporción inercia dintel-pilar. Estas circunstancias justifican que tratemos de calcular el coeficiente de pandeo en pórticos con dimensiones luz-altura habituales en los triarticulados de madera y con proporciones entre inercias de 0,85, 1 y 1,15.
Se puede observar, a la vista del análisis de tendencias, que estimando estos coeficientes de pandeo para una sola pendiente (la más baja) se simplifica una variable y estaríamos del lado de la seguridad. Eliminando esta variable se consigue que el estudio del coeficiente de pandeo de pórticos triarticulados fuera mucho menos farragoso del que resultaría bajo estas otras condiciones.
Metodología de trabajo
Para obtener una ecuación que pueda indicar el comportamiento del coeficiente de pandeo se necesitan una serie de datos (resultados) sobre los que se pueda realizar una regresión.
Para evitar que estos datos puedan venir sesgados por su propia naturaleza y puedan así condicionar la posterior distribución de los mismos, se deben obtener como es lógico con un sesgo real.
Sabemos que la carga más interesante para el estudio del pórtico, y ya fijada anteriormente, es la uniforme vertical, recordándose aquí que para el valor del coeficiente de pandeo no afecta al tipo de carga sólo la proporción que tengan entre las mismas.
Las variables que definen a cualquier pórtico tras el estado de carga son la luz, altura de pilares, la pendiente y las relaciones entre inercias reales.
Tras la realización del análisis de tendencias e influencia de estas variables, se puede tener un criterio para decidir a qué parámetros de los mencionados se les debe dar más peso en el estudio debiendo estar conjugados con la realidad.
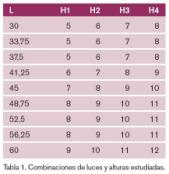
Estos condicionantes hacen que busquen los resultados para luces de pórticos triarticulados entre 30 y 60 m con un intervalo de 3,75 m, alturas de pilares variables en función de la luz para tener así las situaciones más reales y que van desde 5 m (pórtico de 30 m) hasta 12 m (pórtico de 60 m). No obstante, cada luz de pórtico se combina con cuatro alturas. La pendiente será única para todos los casos y de valor 5º, pues así estaremos del lado de la seguridad. Las inercias se toman dentro del campo de variación lógico, esto es, los pórticos tendrán inercias relativas de 0,85 – 1 – 1,15. De esta forma se obtiene un total de 108 casos de estudio que deberemos procesar adecuadamente para así tener posterior-mente una ecuación que nos permita calcular el coeficiente de pandeo para pórticos de una altura.
La combinación de luces-alturas se puede apreciar en la tabla 1.
La naturaleza de los datos iniciales hace que, en rigor, los resultados sólo sean aptos para pórticos triarticulados de madera.
Obtención de la ß de pandeo de pórticos triarticulados de madera
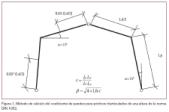
Una vez modelizados los 108 pórticos y estimados sus coeficientes de pandeo, tenemos la misión de extraer una ecuación que recoja la ley de este coeficiente de pandeo. Los antecedentes que tenemos son los de las normas DIN, que ofrecen el valor del coeficiente de pandeo en función de un parámetro “c” tal y como se observa en la figura adjunta, así como los métodos de estimación del coeficiente de pandeo para pórticos de varias alturas (método de Julian-Lawerence y método de Wood)
En ellos se pueden observar varias circunstancias:
1. En el caso de pórticos triarticulados de un piso, el coeficiente de pandeo aumenta con la luz e inercia de pilares, así como disminuye con la altura de los pilares y la inercia de los dinteles (magnitud auxiliar c de las normas DIN ).
2. En los métodos de Julian y Lawrence y el de Wood el coeficiente de pandeo depende exclusivamente de las variables: longitud de pilares y vigas, y sus inercias. Es muy importante notar que en ellos:
– Influye la proporción entre las longitudes de las barras.
– Influye la proporción entre inercias.
3. En el análisis de tendencias también se reflejó esta situación.
4. En las ecuaciones de pórticos de una altura y un vano el coeficiente ß depende de un solo parámetro (c+6s)= c elevado al cuadrado y a uno más, una constante, y finalmente todo elevado a 0,5.
Llegados a este punto y tras los antecedentes, se deben hacer una serie de reflexiones:
1. Las variables más usualmente empleadas en los métodos de cálculo del coeficiente de pandeo son longitud de dintel y pilar, inercia del dintel e inercia del pilar para una pendiente concreta. En su defecto, se aporta la misma información con luz, altura de pilares, inercia del dintel e inercia del pilar. Esto es así en el caso de pórticos de una altura.
2. Todos los métodos parametrizan estas variables en una o dos de modo que luego trabajan con funciones tipo f(x) o f(x,y).
Tras esto se concluye que para obtener una ecuación que nos dé el coeficiente de pandeo éste debe (en principio) depender de un parámetro que englobe en él a las otras variables, de modo que éste sea susceptible de aplicársele la regresión que nos dé los mayores coeficientes de correlación múltiple, el cuadrado de este coeficiente y el coeficiente de correlación ajustado.
Vistas las ecuaciones existentes y las posibles, parece lógico pensar que una ecuación polinómica o una potencial serán a priori las que se adapten mejor a la distribución del coeficiente de pandeo, pues para los casos de pórticos de una altura tenemos un solo parámetro integrado en polinomios de segundo grado que posteriormente se elevan a 0,5.
Para facilitar la regresión es muy importante concebir bien este parámetro; por esta razón éste debe reflejar las características que se le observan al fenómeno del pandeo, para que los pórticos semejantes entren con el mismo valor en la ecuación que se aplique:
1. debe respetar que, a igualdad de proporción luz-altura, el valor del parámetro debe ser el mismo.
2. a igualdad de condiciones para la misma proporción de inercias dintel pilar también debe tener el mismo valor para entrar en la fórmula de la regresión con la misma cifra y dar el mismo coeficiente de pandeo.
Estas dos cuestiones son cruciales para estar bien encaminados y tener una mayor probabilidad de encontrar una ecuación válida.
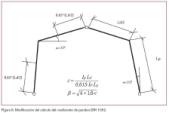
Con estas ideas se ponen las bases para la parametrización de las variables, pero antes de darle una forma definitiva conviene analizar la siguiente situación. Por un lado es sabido que la magnitud auxiliar “c”, definida en la norma DIN para los pórticos triarticulados de un piso, respeta los criterios mencionados arriba en cuanto a las relaciones de las variables. Por eso resulta muy interesante comparar los coeficientes de pandeo de estos dos casos: dos pórticos triarticulados con carga uniformemente distribuida, sin pendiente y de las características definidas en la figura 3.
Ambos pórticos tienen en común que la magnitud auxiliar “c” que se define en la DIN en las ecuaciones de pórticos de una altura tiene el mismo valor, c=7,5. El siguiente paso consiste en conocer la versatilidad de este parámetro “c” para conocer cómo se adapta a nuestra situación. Si fuera un buen parámetro para nosotros, nos debería dar para el mismo valor “c” un coeficiente de pandeo prácticamente igual, pues con él entraríamos en una ecuación que desconocemos con el mismo parámetro.
El resultado es sorprendente, pues se comprueba que para el primer caso el coeficiente de pandeo es ß=5,207 mientras que para el segundo es ß=4,486. Esta diferencia permite concluir que la magnitud auxiliar “c” no nos es todo lo aplicable que se debería para nuestra ecuación, por lo que no la emplearemos.
Debe pensarse entonces que la aportación de la relación luz altura al incremento del coeficiente de pandeo no es el mismo que el de la relación entre inercias. Es precisamente esta última conclusión la que indica que manteniéndose las condiciones concluidas hasta ahora, para una pendiente dada, deben remunerarse por separado las influencias del incremento luz /altura y las del incremento inercia del pilar / inercia del dintel.
Por esta razón se parametrizan las variables luz, altura de pilares, inercia de dinteles e inercia de pilares del siguiente modo:
X = a1 ( Luz / altura)m + a2 (I. pilar/ I dintel) n
Esta forma se explica por las siguientes razones:
1. Respeta las condiciones definidas de las dos relaciones incrementales, de modo que ahora ambos incrementos ponderan por separado a la hora de definir un coeficiente de pandeo.
2. Mantiene la adimensionalidad que hasta ahora también se venía dando en los parámetros que afectaban al coeficiente de pandeo.
3. Cabe esperar también que la función donde se implemente sea creciente con el valor del parámetro, concordando así con la forma de otras ecuaciones.
4. Los exponentes “m” y “n” servirán para reflejar mejor el peso de estas proporciones aumentando o disminuyendo estos cocientes en función de que sean mayores o menores que la unidad.
5. Con esta forma de parámetro la siguiente fase de la investigación es iterar con los valores de a1, a2, m y n hasta tener la regresión que nos dé los mayores coeficientes de correlación múltiple, el cuadrado de este coeficiente y el coeficiente de correlación ajustado.
Los cálculos estadísticos se hicieron con el programa estadístico SPSS 10.1 con el que se ajustaron los valores para conjugar los mejores grados del polinomio y mayores coeficientes de correlación en función de los coeficientes, así como también para una regresión tipo potencial.
Finalmente, se obtuvo la curva que se representa en la figura 4.
Ecuación que resulta de parametrizar con a1=6; a2=11,15; m= 0,79 y n=0,88.
Este parámetro X puede disgregarse en dos magnitudes auxiliares:
a = 6 · (Luz / H)0,79
b = 11,15 · (Ipilar / Idintel)0,88
Análisis estadístico de la ecuación
En este apartado se reflejan los resultados de los parámetros estadísticos de control de la regresión como los coeficientes de regresión, los contrastes de hipótesis de dependencia de la función respecto de la variable independiente.
Los resultados estadísticos, coeficientes de correlación y tabla Anova, se resumen en la tabla 2.
Análisis de errores, influencia de las variables en el error y márgenes de validez
Este apartado tiene el objeto de adaptar la ecuación teórica a una real que se adapte a sus condicionantes, de modo que no se cometan errores del lado de la inseguridad. Por esta razón se calculó la diferencia entre el ß del m.e.f. y el ß de la fórmula, obteniéndose un coeficiente de pandeo correcto si el ß de la fórmula se incrementaba un 2%.
El siguiente aspecto a tratar es definir los márgenes de las relaciones entre las que se obtuvo la ecuación, que es donde se garantiza el buen funcionamiento de la misma.
Por un lado, se tiene la relación luz/altura de pilares que osciló entre 30/8, esto es 3,75 en su menor valor hasta 37,5/5, 7,5, en su mayor valor.
Esto indica que debe acotarse la magnitud “a” entre:
a = 6 · (Luz / H)0,79 para 3,75 < (Luz / H) < 7,5
Las relaciones entre inercias mínima y máxima con que se trabajó fueron 0,85 y 1,15 con lo que estos valores deben acotar la magnitud auxiliar b.
b = 11,15 · (I pilar / I dintel)0,88 para 0,85 < (I pilar / I dintel) < 1,15
El mayor y menor valor de X fue 42,08 y 26,71
Finalmente y de cara a estar siempre del lado de la seguridad, debido a que el error máximo cometido fue del 1,03% del lado de la inseguridad, se pondera la ecuación en un 2%. El mejor modo de conseguirlo es multiplicar toda la ecuación por 1.000 para tenerla con una forma más convencional y dividirla entre 980 (en vez de entre 1.000), de modo que realmente se pondera en un 2,04%.
Tras todo esto la ecuación queda tal y como se aprecia en la figura 5.
Ecuación alternativa consistente en modificar la de la norma DIN 1052.
En los resultados anteriores se le achacaba a la ecuación de la norma DIN que recogía en ella valores menores de los que se obtienen por los elementos finitos. Esto es posible porque se trata de una ecuación deducida para pórticos sometidos a cargas puntuales y no a cargas uniformes. Sin embargo, cabe la posibilidad de generar una nueva ecuación desde ésta de modo que dé una mayor versatilidad a la hora de calcular el coeficiente de pandeo para cargas uniformes. Esto se consigue dividiendo el parámetro c entre 0,615.
La fórmula quedaría, por tanto, como se aprecia en la figura 6.
Que es equivalente a aplicar la anterior pero considerando los dinteles con una inercia del 61,5% de la real.
Conclusiones
1. Se desaconseja adaptar las situaciones de carga de la norma DIN para calcular el coeficiente de pandeo en las situaciones de carga uniformemente distribuidas.
2. Las pendientes habituales a dos aguas tienen un efecto mínimo sobre el coeficiente de pandeo.
3. Se puede obtener una ecuación que se adapte al coeficiente de pandeo de pórticos de una altura triarticulados de madera sometidos a cargas verticales uniformes, con perfiles rectos y con la misma sección en dinteles y pilares.
4. La diferencia de valor del coeficiente de pandeo entre la norma DIN y el m.e.f., del lado de la inseguridad, es mayor cuanto mayor es la proporción luz altura de pilares y proporción entre inercias (parámetro X).
5. Se estima que la pérdida de rigidez del dintel por efecto del axil es del 38,5% si se comparan los pórticos triarticulados sometidos a cargas puntuales en los pilares frente al sometido a cargas verticales uniformes.
6. Existe una fórmula alternativa para pórticos triarticulados de madera a la aquí propuesta y que consiste en modificar la fórmula de la DIN 1051 y en disminuir la inercia del dintel en un 38,5%.
Referencias
1. Documento Básico de Seguridad Estructural Madera DB SE-M Código Técnico de la Edificación. Ministerio de la Vivienda. Madrid 2006
2. Eurocódigo 5: “Proyecto de estructuras de madera” Parte 1-1:Reglas generales y reglas para la edificación. AENOR. 1997.
3. Argüelles Álvarez R. y Arriaga Martitegui F. “Estructuras de madera. Diseño y cálculo” AITIM. Madrid. 2001.
4. Vidal López P.,Guaita Fernández M, López Villar M.J. y Couto Yáñez,A. “El coeficiente ß de pandeo en pórticos biarticulados metálicos de una altura: propuesta de ecuación mediante el m.e.f.”. Ingeniería Civil nº 117. pp. 107-114 C.E.D.E.X. M. de Fomento.
5. Sancho Aznal, J.Mª. “Teoría del MEF aplicada a problemas no lineales”. Curso de especialización superior en Teoría y Aplicación del M.E.F. 1994/1995. 2.000.
RESUMEN
Los pórticos triarticulados de una altura son una de las tipologías más frecuentes en estructuras de madera laminada. Existe desde hace poco una nueva normativa específica para el cálculo de estas estructuras, el DB SE-M, que pone de manifiesto el creciente interés por estas estructuras. Como en todas las normativas de estructuras, el empleo del coeficiente de pandeo es necesario, por lo que debemos acudir a la metodología de la DIN 1052 que presupone el pórtico sometido a dos cargas puntuales. En este artículo se estudia el pandeo de estos pórticos sometidos a cargas verticales uniformes y se obtiene una fórmula para el cálculo de este coeficiente de pandeo. Por último, se ofrece una modificación de la norma DIN 1052 que aproxime mejor el coeficiente de pandeo a cargas verticales uniformes.
Palabras clave: Estructuras de madera, pórticos triarticulados, pandeo.